SCI论文(www.lunwensci.com):
摘 要 : 文章对 2022 年新高考全国Ⅰ卷第 21 题进行探究,给出两种解法,并将试题推广,得到椭圆、双曲线和抛物线的一般性结论.
关键词 : 高考试题; 圆锥曲线; 探究; 推广
1 题目呈现与解答
题目 (2022 年新高考全国Ⅰ卷第 21 题) 已知点 A(2,1) 在双曲线
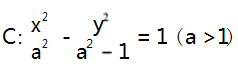
上,直线 l 交 C 于 P、Q 两点,直线AP,AQ 的斜率之和为0.
( 1) 求 l 的斜率 ;
(2) 若 tan∠PAQ = 2 ,求ΔPAQ 的面积.
本题的解法较多,下面给出其中的两种解法.
解法 1 ( 1) 将点 A(2,1) 代入双曲线方程,得
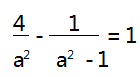
化简,得 a4 -4a2 + 4 = 0,解得 a2 = 2
故双曲线 C 的方程为
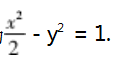
由题可知直线 l 的斜率存在,设直线 l 的方程为 y = kx + m,设 P(x1 ,y1 ) ,Q(x2 ,y2 ) .
化简整理,得(k + 1) (m + 2k -1) = 0.
当 m + 2k -1 = 0,即 m = 1 -2k 时,直线 l 的方 程为 y = kx + 1-2k = k(x-2) + 1,此时直线 l 过点 A(2,1) ,不符合题意,故 m + 2k -1 ≠0.
所以 k + 1 = 0,即 k = -1.
所以直线 l 的斜率为-1.
(2) 不妨设直线 AP 的倾斜角为锐角且为 α , 由 于直线 AP,AQ 的斜率之和为 0,故直线 AP,AQ 的倾 斜角互补,所以 2α + ∠PAQ = π , 即∠PAQ = π - 2α.
评注 解法 1 通过联立直线与双曲线方程,利 用韦达定理及直线斜率的定义进行求解.运算量虽 不小,但方法是解析几何中的常用方法,这种通性通 法在数学解题中有重要作用.所以在平时的教学中 要注重一般性的解题规律和方法( 即通性通法) ,要 重视知识的生成过程,尽量创设问题情境引导学生探究知识,培养学生分析问题、解决问题的能力.
解法 2 ( 1) 由解法 1 可知,双曲线 C 的方程为
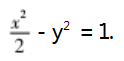
(2) 不妨设 α 为锐角,由于直线 AP、AQ 的斜率 之和为 0,故直线 AP、AQ 的倾斜角互补.
所以 2α + ∠PAQ = π .
即∠PAQ = π - 2α.
评注 一般情况下,圆锥曲线大题的解答过程 往往涉及繁冗运算,要减少圆锥曲线的运算量,规避 运算风险,算理就显得非常重要.解法 2 利用直线的 参数方程,其代数变形较简单,运算量少,解题过程 比解法 1 更简洁.
2 问题的提出
问题 1 在试题中,若将点 A (2,1 ) 改为其它 值,则直线 l 的斜率为多少?
问题2 在试题中,若将点 A(2,1) 改为 A(x0,y0 ) (y0 ≠0) ,并将双曲线一般化,则直线 l 的斜率为多少?
问题 3 在试题的问题( 1) 中,若将试题改为 :点 A(2,1) 在双曲线
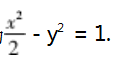
上,直线 l 交 C 于 P,Q 两点,且直线 l 的斜率为-1,则直线 AP、AQ 的斜 率之和为多少?
问题 4 在问题 2 或问题 3 中,若将双曲线改 为椭圆或抛物线,又有什么结论?
3 试题问题( 1) 的推广与类比性质
结合上述问题,经探究,可得到试题问题( 1) 的 推广与类比性质 :
结论 1 已知点 P(x0 ,y0 ) (y0 ≠0) 在椭圆 C:
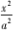
+

= 1(a >b >0 ) 上,M、N 是椭圆 C 上的两个动点,若直线 PM、PN 的斜率分别为 k1 、k2 ,则 k1 + k2 =0 的充要条件是直线 MN 的斜率为

.
结论 2 已知点 P(x0 ,y0 ) (y0 ≠0) 在双曲线

上,M、N 是双曲线 C 上的两个动点,若直线 PM、PN 的斜率分别为 k1 ,k2 ,则 k1b2 x0+ k2 = 0 的充要条件是直线 MN 的斜率为
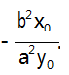
结论 3 已知点 P(x0 ,y0 ) (y0 ≠0) 在抛物线 C: y2 = 2px(p>0) 上,M、N 是抛物线 C 上的两个动点, 若直线 PM、PN 的斜率分别为 k1 ,k2 ,则 k1 + k2 = 0的充要条件是直线 MN 的斜率为

评注 ①结论 1 至结论 3 的证明,可以参照试 题( 1) 的解答,限于篇幅,不再给出.
②由结论 2 可知,当 P(x0 ,y0 ) = A(2,1) ,双曲线方程为

时,则直线 PQ( 即直线 l) 的斜率为
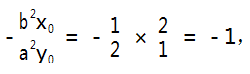
,这正是高考题的问题( 1) .
4 探究延伸
结论 1 至结论 3 均是 k1 + k2 = 0 与直线 MN 的 斜率之间的关系.那么在一般的条件下,直线 PM、 PN、MN 三者的斜率之间有什么联系? 此时,能否求得ΔPMN 的面积?
经进一步探究,可得到如下结论 :
结论 4 已知点 P (x0 ,y0 ) (y0 ≠0 ) 在曲线 C: Ax2 + By2 = 1(AB≠0) 上,M、N 是曲线 C 上的两个动 点,若直线 PM、PN、MN 的斜率分别为 k1 、k2 、k3 ,则
证明 因为平移不改变直线的斜率及图形的面积,故平移坐标系,使得点 P 为坐标原点,则曲线 C变为
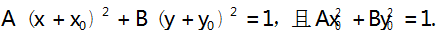
此时直线 PM 的方程为 y = k1 x,设 M(xM,yM ) , N(xN,yN ) .
结论 5 已知点 P(x0 ,y0 ) (y0 ≠0) 在抛物线 C:y2 = 2px(p>0) 上,M、N 是抛物线 C 上的两个动点, 若直线 PM、PN、MN 的斜率分别为 k1 、k2 、k3 ,则
证明 因为平移不改变直线的斜率及图形的面 积,故平移坐标系,使得点 P 为坐标原点,则曲线 C变为(y + y0 ) 2 = 2p(x + x0 ) ,且 y = 2px0 .
此时直线 PM 的方程为 y = k1 x,设 M(xM,yM ) , N(xN,yN ) .
评注 当 P(x0 ,y0 ) = A(2,1) ,双曲线方程为
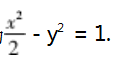
时,则 A =

,B = -1,kAP + kAQ = 0,且由解 法 1,可知 kAP =

,kAQ = -

.分别代入结论 4,可得直线 PQ 的斜率为 -1,ΔPAQ 的面积为
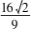
,这正是高考题的情形.
高考试题是精心之作,每年的高考题在命题角 度、题型、难度等方面都进行了充分考量,是知识、能 力和思想方法的载体,具有典型性、示范性和权威 性.高考试题除了具有测试与选拔功能外,还具有良 好的教学功能,要了解高考动向,把握高考脉搏.高 考试题的研究是重要的路径,所以在复习中要加强 高考题的渗透,通过高考真题的训练体会命题思想, 善于作解后反思和方法的归类,并对试题进行挖掘、 拓展、引申,扩大高考题的辐射面,从而实现高考试题功能的最大化、最优化.
参考文献 :
[1]林国红.一道圆锥曲线竞赛试题的推广探究 [J].数学通讯,2022 (04) : 44-45,55 .
[2]林国红.圆锥曲线中两根不对称问题的处理方法[J].高中数学教与学,2018(19) : 12 -14 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/72827.html
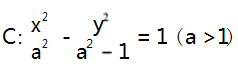 上,直线 l 交 C 于 P、Q 两点,直线AP,AQ 的斜率之和为0.
上,直线 l 交 C 于 P、Q 两点,直线AP,AQ 的斜率之和为0.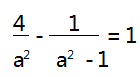 化简,得 a4 -4a2 + 4 = 0,解得 a2 = 2
化简,得 a4 -4a2 + 4 = 0,解得 a2 = 2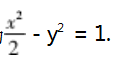





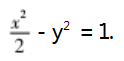





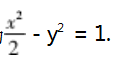 上,直线 l 交 C 于 P,Q 两点,且直线 l 的斜率为-1,则直线 AP、AQ 的斜 率之和为多少?
上,直线 l 交 C 于 P,Q 两点,且直线 l 的斜率为-1,则直线 AP、AQ 的斜 率之和为多少?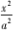 +
+  = 1(a >b >0 ) 上,M、N 是椭圆 C 上的两个动点,若直线 PM、PN 的斜率分别为 k1 、k2 ,则 k1 + k2 =0 的充要条件是直线 MN 的斜率为
= 1(a >b >0 ) 上,M、N 是椭圆 C 上的两个动点,若直线 PM、PN 的斜率分别为 k1 、k2 ,则 k1 + k2 =0 的充要条件是直线 MN 的斜率为 .
. 上,M、N 是双曲线 C 上的两个动点,若直线 PM、PN 的斜率分别为 k1 ,k2 ,则 k1b2 x0+ k2 = 0 的充要条件是直线 MN 的斜率为
上,M、N 是双曲线 C 上的两个动点,若直线 PM、PN 的斜率分别为 k1 ,k2 ,则 k1b2 x0+ k2 = 0 的充要条件是直线 MN 的斜率为 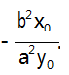

 时,则直线 PQ( 即直线 l) 的斜率为
时,则直线 PQ( 即直线 l) 的斜率为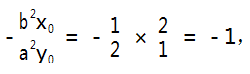 ,这正是高考题的问题( 1) .
,这正是高考题的问题( 1) .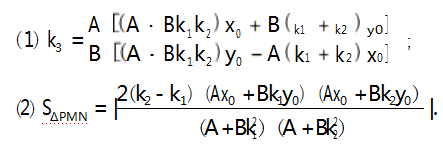
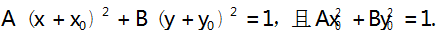

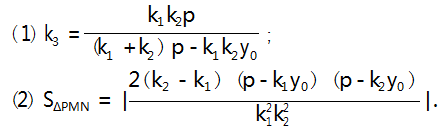


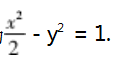 时,则 A =
时,则 A =  ,B = -1,kAP + kAQ = 0,且由解 法 1,可知 kAP =
,B = -1,kAP + kAQ = 0,且由解 法 1,可知 kAP =  ,kAQ = -
,kAQ = -  .分别代入结论 4,可得直线 PQ 的斜率为 -1,ΔPAQ 的面积为
.分别代入结论 4,可得直线 PQ 的斜率为 -1,ΔPAQ 的面积为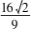 ,这正是高考题的情形.
,这正是高考题的情形.