平中蕴奇探究本质 — 一道2022 年高考试题的溯源与延伸论文

 

SCI论文（www.lunwensci.com）：

　　摘  要 :有些看似背景平淡的高考试题 ,但往往平中蕴奇 ,这些试题有着丰富的思想方法内涵 , 反映出数学本质性的东西 , 多角度进行分析、探究 ,对提高数学思维能力大有裨益. 本文就 2022 年高考全国甲卷理科第 10 题予以探究.

　　关键词:2022 年 ; 高考试题;溯源;延伸

　　1 试题呈现

　　题目  椭圆 C : + = 1 ( a > b > 0) 的左顶点为 A ,点 P , Q 均在 C 上 , 且关于 y 轴对称. 若直线AP ,AQ 的斜率之积为 ,则 C 的离心率为(       ) .
 

　　A.        B.        C.        D.
 

　　分析  设 P ( x1 ,y1 ) ,则 Q ( - x1 ,y1 ) ,根据斜率公式结合题意可得=  ,再根据+ =1 ,将 y1  用 x1   表示 , 整理 , 再结合离心率公式即可 得解.
 

　　解析  由 题 设 知 A ( - a ,0 ) , 设 P ( x1 ,y1 ) , 则 Q( - x1 ,y1 ).

　　所以   

　　故 kAP   ·kAQ  =  · =  =  .又+ = 1 ,

　　

　　所以椭圆 C 的离心率 e =  = 1 - = .
 

　　故选 A.

　　若将点 A 换为右顶点 ,有相同的答案.

　　2 试题溯源

　　该试题源于教材 ,是由人教普通高中课程标准实验教科书( A版) 数学选修 2 - 1 两道题目改编而成的.

　　题 1    ( 人教 A 版数学选修 2 - 1 第 41 页 2. 2 例 3) 如图 1 所示 ,设点 A ,B 坐标分别是 ( - 5 ,0 ) , (5 ,0) ,直线 AM ,BM 相交于点 M ,且它们的斜率之积是 - ,试求点 M 的轨迹方程.
 

图 1
 

　　解析  解答过程见课本. 轨迹方程为 +  =1(x≠ ± 5) ,轨迹是除去 A ,B 两点的椭圆.
 

　　题 2    ( 人教 A 版数学选修 2 - 1 第 55 页的探 究题) 如图 2 , 点 A ,B 坐标分别 是 ( - 5 ,0 ) , ( 5 , 0 ) ,直线 AM ,BM 相交于点 M ,且它们的斜率之积是  ,试求点 M 的轨迹方程 ,并由点 M 的轨迹方程判断轨迹的形状 ,与 2 . 2 例 3 ( 上述第 1 题) 比 较 ,你有什么发现.
 

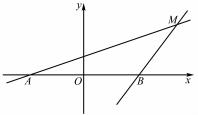
图 2
 

　　解析  设点 M 的坐标为(x ,y) ,依题意 ,得

　　

　　显然点 M 的轨迹是除去 A ,B 两点的双曲线.

　　教材是高考命题的生长点 ,立足教材 ,坚持对教 材的回归 ,将教材例题、习题重新组合、改编和加工 为高考试题 ,是高考命题的一个重要趋势. 因此 ,在 复习备考的过程中要注意回归教材 ,通过对教材例、 习题的探索变式、拓展推广 ,对解题思路进行内化、 深化的训练 ,达到把握其实质 ,掌握其规律 ,规范其 步骤的目的 ,进而使数学思维得到升华 ,促进数学核 心素养的形成和发展.

　　3 延伸探究

　　若试题的题设条件不变 ,将直线 AP ,AQ 的斜率之积的“”换为 一 般 情 形 的 数 值 m ( 0 < m <1 ) ,可有 :
 

　　命题 1   椭圆 C :+  = 1(a > b > 0) 的左( 或右) 顶点为 A ,点 P , Q 均在 C 上 ,且关于 y 轴对称. 若直线 AP ,AQ 的斜率之积为 m (0 < m < 1) ,则 C 的离心率为 .

 

　　证明按上面试题的解法进行 ,这里从略. 将命题 1 类比、延伸到双曲线 ,可有 :

　　命题 2   双曲线 C :  -  = 1 ( a > 0 ,b > 0) 的左( 或右) 顶点为 A ,点 P ,Q 均在 C 上 ,且关于 y 轴 对称. 若直线 AP ,AQ 的斜率之积为 - m (0 < m < 1) ,则 C 的离心率为.

 

　　证明  以 A 为左顶点为例来证明.

　　不妨设 A ( - a ,0 ) ,P ( x1 ,y1 ) ,则Q ( - x1 ,y1 ).

　　所以 kAP  =  ,kAQ  = ,
 

　　kAP   ·kAQ  = · =  = - m.
 

　　又-  = 1 ,

　　则         
  .
　　所以 =b2 )    =m
            .

　　即 = m.
 

　　所以双曲线 C 的离心率 e = = .
 

　　将上述问题改为已知斜率关系的情况下 ,求动 点 P 的轨方程 ,可有:

　　命题 3   设点 A 坐标是 ( - a ,0 )( 或 ( a ,0 )) ,点P ,Q 关于 y 轴对称 ,若直线 AP ,AQ 的斜率之积为( a > 0 ,b > 0) ,则点 P 的轨迹是除去与 x 轴交点的 椭圆.

　　证明  设 P (x ,y ) ,则 Q( - x ,y ) .

　　所以 kAP  = ,kAQ  = .

　　所以 kAP   ·kAQ  =  ·=  . 由题设 ,得=  .
　

　　所以 a2 y2  = - b2 x2  + a2 b2 .

　　所以 b2 x2  + a2 y2  = a2 b2 .

　　所以+  = 1(x ≠ ± a ) .
 

　　故点 P 的轨迹是除去与 x 轴交点的椭圆.

　　命题 4   设点 A 坐标是 ( - a ,0 )( 或 ( a ,0 )) ,点 P ,Q 关于 y 轴对称 ,若直线 AP ,AQ 的斜率之积为- ( a > 0 ,b > 0) ,则点 P 的轨迹是除去与 x 轴交 点的双曲线.
 

　　证明  设 P (x ,y ) ,则 Q( - x ,y ) .

　　所以 kAP  =  ,kAQ  = .
 

　　所以 kAP   ·kAQ  =  · =  .
 

　　由题设 ,得 =-  .
 

　　所以 a2 y2  = b2 x2  - a2 b2 .

　　所以 b2 x2  - a2 y2  = a2 b2 .

　　所以-  = 1(x ≠ ± a ) .

　　故点 P 的轨迹是除去与 x 轴交点的双曲线.

　　命题 3 和命题 4 其实给出了椭圆和双曲线的又 一种形式的定义:

　　平面内关于 y 轴对称的两个动点 P , Q 到定点A ( - a ,0 )( 或( a ,0 )) 的斜率乘积等于的点的轨迹是椭圆;平面内关于 y 轴对称的两个动点 P ,Q 到定点 A ( - a ,0 )( 或 ( a ,0 )) 的斜率乘积等于 -的点的轨迹是双曲线.

 

　　更一般地 ,有 :

　　平面内关于 y 轴 对 称 的 两 个 动 点 P , Q 到 定 点A ( - a ,0 )( 或 ( a ,0 )) 的 斜 率 乘 积 等 于 常 数 m ( m ≠0 ,m ≠ - 1 )的点的轨迹是椭圆或双曲线. 当 常数 m > 0 时 ,且 m ≠ 1 时 , 轨迹是除去与 x 轴交 点的椭圆;当常数 m < 0 时 ,轨迹是除去与 x 轴交 点的双 曲 线. 其 中 定 点 A 是 椭 圆 或 双 曲 线 的 左 顶点.

　　对高考试题的多角度探究 , 就是指对问题从 不同视角 来 审 视 , 以 不 同 的 切 入 点 探 究 问 题 , 其 实质是对试题的“ 二次开发”. 通过对试题的剖析 和思考 ,展开问题的来龙去脉和知识间的纵横联 系 ,站在一定的高度去思考问题 , 突出数学本质 , 使知识达 到 融 会 贯 通 , 使 思 维 得 到 升 华 , 进 而 优 化数学思维品质.

　　参考文献 :

　　[ 1 ] 2022 年普通高等学校招生全国统 一 考试( 甲 卷)数学(理科) .