SCI论文(www.lunwensci.com):
摘要:2021年高考命题要坚持立德树人,加强对学生德智体美劳全面发展的考查和引导.要优化情景设计,增强试题开放性、灵活性、引导减少死记硬背和“机械刷题”现象.基于高考指挥棒以及新课程新教材实施,对学生能力培养,理解分析题目,运算能力都有着较高的要求.圆锥曲线的课堂是学生运算能力的主战场,同时对教师也提出了更高要求,通过教师在课堂上计算板演,学生模仿训练,以提高学生对圆锥曲线基本的运算能力.
关键词:圆锥曲线;基本不等式;新教材
高中数学圆锥曲线是一个重要的数学模型,有着非常好的几何性质.用解析的方法研究圆锥曲线,体现了代数与几何的有机结合,在教学过程中应充分反映其价值,在激发学习兴趣的同时,增强学生用数学的意识和能力.本文结合教学案例剖析运算技巧.
1教学内容分析
圆锥曲线是高中数学的重要内容.众所周知,圆锥曲线的运算量很大,在新教材新高考卷中依然作为难题出现且得分率较低.在高中数学圆锥曲线中以数形结合为首要思想方法,同时兼备各种计算技巧.
2教学过程
在2020年无锡市普通高中秋学期高二期终教学质量抽测卷中的22题,本题得分率很低.(如图1)
(1)求椭圆C的方程;
(2)设平行于OD的直线l与椭圆C交于A,B两点.
①线段AB的长度是否有最大值?并说明理由;
②若直线DA,DB与x轴分别交于M,N两点,记M,N的横坐标为m,n,求证:m+n为定值.
解析 (1)

,详解略.
(2)①略②学生作答情况(如图2)
由学生对22题(2)②答题情况可以看出,大部分学生对圆锥曲线分析问题,解决问题还是比较欠缺的.
参考答案与优秀学生答案:(如图3,如图4)

评注我们参考优秀学生作答情况与参考答案对比后,发现学生消元y时计算更简洁.所以在圆锥曲线中,运算方面选择方向很重要.
(1)求椭圆方程;
(2)证明:k1 k2=

(3)当直线DM过定点(1,0)时,求


的最小值.
解析(1)
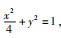
详解略.(2)略
(3)设直线
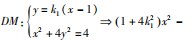

评注:解法1通过二次函数求最值,解法2应用基本不等式求最值,对比两种解法对数据的处理,显然利用基本不等式可以更快速得出结论.
下面看下学生做题情况:(如图5,如图6)

评注通过对学生答题情况分析,学生对圆锥曲线答题上还是很欠缺的,学生对数据分析处理应提出更高的要求.
变式训练古希腊数学家阿基米德利用“逼近法”得到椭圆的面积,即椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积.若椭圆C1的中心为坐标原点,焦点F1,F2均在x轴上,椭圆
C1的面积为

π,且短轴长为

,椭圆C2:
 =1(0<m<3)与椭圆C1有相同的离心率.
=1(0<m<3)与椭圆C1有相同的离心率.
(1)求m的值与椭圆C1的标准方程;
(2)过椭圆C1的左顶点A作直线l,交椭圆C1于另一个点B,交椭圆C2于P,Q两点(点P在A,Q之间).①求△OPQ面积的最大值(O为坐标原点);
②设PQ的中点为M,椭圆C1的右顶点为C,直线OM与直线BC的交点为N,试探究点N是否在某一条定直线上运动,若是,求出该直线方程;若不是,请说明理由.
解析(1)m=

;椭圆C1:

(详解略)
(2)①详解如下:由题意知:直线AB斜率存在且不为0,所以设直线AB:y=k(x+2);
当且仅当16k
2=12-7k
2,即k
2=

时取“=”.
综上所述:当k
2=
 时,△OPQ面积取到最大值为
时,△OPQ面积取到最大值为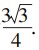 .
.
②轨迹方程:x=

(详解略)
3基于新课程新教材对高中数学课堂教学思考
2020年暑期,我有幸参加江苏省新课程新教材培训,在听完讲座后,充分认识到,此次新课改对学生更加关注核心素养的培养,更加强调学生综合应用知识解决实际问题的能力,这就要求教师在课堂上应更好的把握“教”,要求学生发展数学抽象,逻辑推理,数学建模,数学运算等方面能力.新课程新教材对老师,对学生都是一种考验,尤其一线教师在课堂上要学会转变教学思维.本文主要对学生数学运算上进行一次剖析.
参考文献:
[1]张亮.解析几何中定值定点问题“教学实录与反思”[J].中学数学月刊,2014(2):33-35.
[2]余小高.大数据环境中微课程个性化学习的研究[J].中国教育信息化,2015(13):18-21,26.
[3]孔邦新.一道解析几何题的变式探究及教学思考[J].中国数学教育,2016(24):53-56.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/41095.html

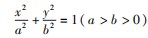 的离心率为
的离心率为 ,且过定点D
,且过定点D
 ,详解略.
,详解略.
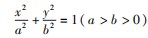 点D,M,N为C上的动点.O,M,N三点共线,离心率e=
点D,M,N为C上的动点.O,M,N三点共线,离心率e=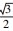 一条准线方程为x=
一条准线方程为x= 直线DM,DN的斜率分别为k1,k2(k1 k2≠0).
直线DM,DN的斜率分别为k1,k2(k1 k2≠0).

 的最小值.
的最小值.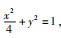 详解略.(2)略
详解略.(2)略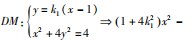


 π,且短轴长为
π,且短轴长为 ,椭圆C2:
,椭圆C2: =1(0<m<3)与椭圆C1有相同的离心率.
=1(0<m<3)与椭圆C1有相同的离心率. ;椭圆C1:
;椭圆C1: (详解略)
(详解略)
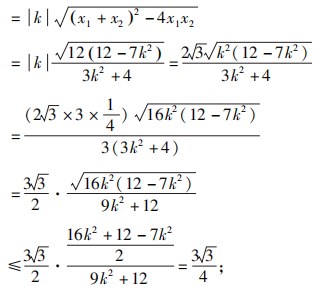
 时取“=”.
时取“=”. 时,△OPQ面积取到最大值为
时,△OPQ面积取到最大值为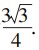 .
. (详解略)
(详解略)