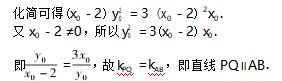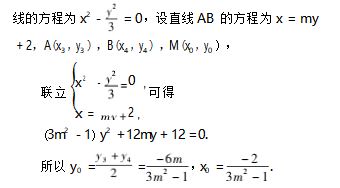SCI论文(www.lunwensci.com)
摘 要 : 本文以 2022 年新高考Ⅱ卷的第 21 题为例,从通法到巧解呈现了解决解析几何问题的 常规方法,并结合曲线系方程这一试题命制背景,给出了一般性的结论.
反思 上述解法是处理圆锥曲线解答题的通 法,把点坐标作为参数,设出相关直线的方程,再转 化已知条件,最终得出结果.此法的计算量较大,深 度考查了学生数学运算与逻辑推理的核心素养,或 许这就是命题者的初衷.
解法 2 设表示双曲线两条渐近线的退化双曲
( 困难 : 笔者解题至此时,原本尝试用 m 假设直 线 PM,QM 的方程,再与双曲线方程联立,进而证明 命题.想法是美好的,但是复杂的运算( 读者可自行 完成) 直接打消了笔者的念头,转而考虑是否能够 简化运算?
思路重构 : 利用 P,Q 两点的横纵坐标假设直线 PM 与 QM 的方程,并联立它们,得到交点 M 的坐 标,进而得到 P,Q 两点的横纵坐标与参数 m 的关 系 ; 根据已知条件所给的等量关系,设而不求,最终 用 m 表示直线 PQ 的斜率,证明命题.)
反思 上述解法也是处理圆锥曲线解答题的通 法,把斜率( 此法利用斜率的倒数) 作为参数,设出 相关直线的方程,利用了韦达定理与点差法,整体对 待交点坐标,设而不求,得到结论.相比求出交点坐 标的方法,有效地减少运算量.
反思 本解中,设出 A,B,P,Q 四个点的坐标, 利用 P,Q 两点的坐标满足的 4 个方程,构造方程- 6x0 x + 2y0 y + 3x0(2) -y0(2) + 3 = 0.得到过 P,Q 两点的直线方程,通过点差法得点 M 的坐标与直线 AB 的 斜率关系,最终得到 kPQ = kAB,命题得证.这种设点 的解法,直接利用点 M 的横纵坐标表示直线 PQ 的 方程,同样大幅减少运算量.
对比以上三种解法,显然解法 3 的运算量是最 少的.那么这样巧妙的解法又是从何而来?
只有教师在日常教学中,立足“本手” ——— 重视 通性通法的教学,给足学生时间修炼数学的“童子 功” ; 探寻“妙手” ——— 重视教材,回归教材,挖掘课 本试题的潜在价值( 即课本试题的组合、演变、拓展 与延伸) ,不仅要让学生知其所以然,还要知何由以 知其所以然 ; 兼顾“本手”和“妙手” ,方能高效复习.
参考文献 :
[1] 陈 忠.利用曲线系方程解决 定 点、定值 问题 [J].中学数学月刊,2014 (09) : 63-65 .
[2]章建跃,李增沪.普通高中教科书数学·选择性必 修(A 版) [M].北京:人民教育出版社,2019.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/71196.html