SCI论文(www.lunwensci.com):
摘要:本文以2022年深圳市高三调研考试解析几何试题为例,谈一谈该试题的解法探究以及结论推广.
关键词:一题多解;结论推广;圆锥曲线
1试题呈现
题目已知双曲线

经过点A(2,0),且点A到C的渐近线的距离为
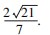
(1)求双曲线C的方程;
(2)过点P(4,0)作斜率不为0的直线l与双曲线C交于M,N两点,直线x=4分别交直线AM,AN于点E,F.试判断以EF为直径的圆是否经过定点,若经过定点,请求出定点坐标;反之,请说明理由.
2解法探究
2.1第(1)问解析
解析依题意,a=2.
解法1(1)当直线l的斜率存在时,设直线l的方程为
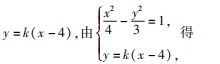
 由对称性可知,以EF为直径的圆过定点,则该点一定在x轴上.
由对称性可知,以EF为直径的圆过定点,则该点一定在x轴上.
解得x=1或x=7.
所以以EF为直径的圆经过点(1,0)和(7,0).
(2)当直线l的斜率不存在时,点E(4,3),F(4,-3),以EF为直径的圆的方程为(x-4)(x-4)+(y-3)(y+3)=0,该圆经过(7,0)和(1,0).
综上所述,以EF为直径的圆经过定点(1,0)和(7,0)
由对称性可知,若以EF为直径的圆过定点,则该定点一定在x轴上,设该定点坐标为T(t,0),则
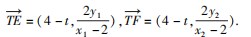
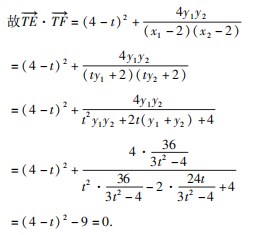
解得t=1或t=7,
所以以EF为直径的圆经过定点(1,0)和(7,0).
3结论延伸
细品解题过程,笔者感觉第(2)问的解答耐人寻味,似乎隐藏一个定点的结论,于是笔者思考,对于一般形式的双曲线,上述问题该如何表示?本例中的定点P、以EF为直径的圆所过的定点、以及a,b之间是否存在着内在联系?如果背景的圆锥曲线换成椭圆、抛物线,是否又有类似的结论呢?基于上述思考,笔者得到如下结论:
证明椭圆结论的证明过程与双曲线类似,这里不再给出.
结论3已知抛物线的顶点为O,过点P(λ,0)(λ>0)的直线l1与抛物线C交于M,N两点,直线AM,AN分别与直线l2:x=λ交于E,F两点,则以EF为直径的圆过定点T(λ±
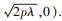

结论4已知抛物线
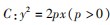
的焦点为F,过点P(λ,0)
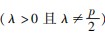
的直线l1与抛物线C交于M,N两点,直线FM,FN分别与直线l2:x=λ交于E,G两点,则当
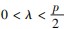
时,以EG为直径的圆过定点

,当

时,以EG为直径的圆过定点


由对称性可知,若以EG为直径的圆过定点,则该定点一定在x轴上,设该定点坐标为T(t,0),则

圆锥曲线中的定点定值问题,可谓一花一世界,一树一菩提,在解题后,若能够静心思考,潜心研究,必能有所收获.
参考文献:
[1]唐洵.揭秘直线与圆锥曲线4大热点问题[J].高中数理化,2014(21):9-11.
[2]中华人民共和国教育部.普通高中数学课程标准(2020年修订版)[M].北京:人民教育出版社,2020
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/45152.html
 经过点A(2,0),且点A到C的渐近线的距离为
经过点A(2,0),且点A到C的渐近线的距离为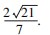
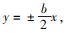
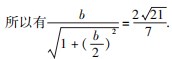

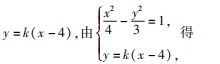

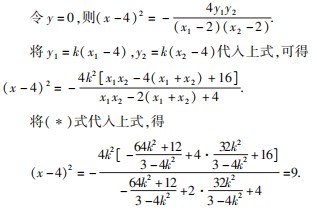

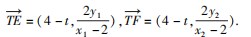
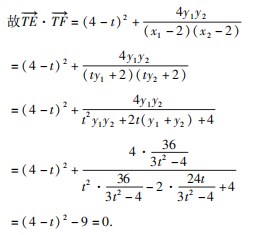
 的右顶点为A,过点P(λ,0)(λ>a)的直线l1与双曲线C交于M,N两点,直线AM,AN分别与直线l2:x=λ交于E,F两点,则以EF为直径的圆过定点
的右顶点为A,过点P(λ,0)(λ>a)的直线l1与双曲线C交于M,N两点,直线AM,AN分别与直线l2:x=λ交于E,F两点,则以EF为直径的圆过定点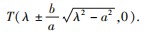
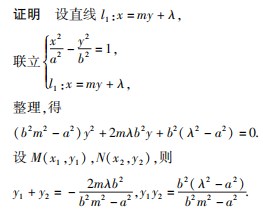

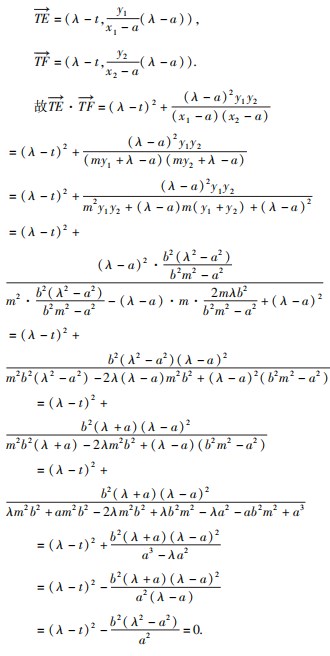

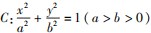 的右顶点为A,过点P(λ,0)(-a<λ<a)的直线l1与椭圆C交于M,N两点,直线AM,AN分别与直线l2:x=λ交于E,F两点,则以EF为直径的圆过定点
的右顶点为A,过点P(λ,0)(-a<λ<a)的直线l1与椭圆C交于M,N两点,直线AM,AN分别与直线l2:x=λ交于E,F两点,则以EF为直径的圆过定点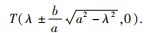
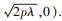

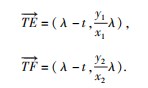

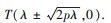
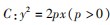 的焦点为F,过点P(λ,0)
的焦点为F,过点P(λ,0)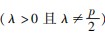 的直线l1与抛物线C交于M,N两点,直线FM,FN分别与直线l2:x=λ交于E,G两点,则当
的直线l1与抛物线C交于M,N两点,直线FM,FN分别与直线l2:x=λ交于E,G两点,则当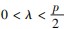 时,以EG为直径的圆过定点
时,以EG为直径的圆过定点 ,当
,当 时,以EG为直径的圆过定点
时,以EG为直径的圆过定点


