SCI论文(www.lunwensci.com):
摘要:本文以一道解析几何求定值问题为例,讲述例题讲解要立足学生的经验,从学生的最近发展区出发,让问题的解答过程流畅、自然,易于学生理解.
关键词:解析几何;经验;特例;最近发展区
解析几何为每年高考考查的热点内容,解析几何的大题基本上以准压轴题的形式出现,常与其他知识交汇命题,主要考查学生的逻辑推理能力和数学运算能力.由于解析几何大题涉及的知识面广、数学运算复杂等原因,导致学生在解答这类题时不知道从哪里下手.因此教师在讲解这类问题时一定要立足学生的经验,从学生最近发展区出发,使得问题的解答流畅、自然,易于学生理解.
1例题呈现
(1)求椭圆C的方程;
(2)设椭圆C的右焦点为F,直线l与椭圆C相切于点A,与直线x=3相交于点B,求证:∠AFB的大小为定值.
又因为

③
所以由①②③,得

所以椭圆C的方程为

(2)显然直线l的斜率存在,设直线l的方程为

 所以切点A的坐标为
所以切点A的坐标为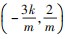 点B的坐标为(3,3k+m).因为右焦点F的坐标为(1,0),
点B的坐标为(3,3k+m).因为右焦点F的坐标为(1,0),
所以∠AFB=90°.
即∠AFB的大小为定值.
以上是资料提供的解答过程,问题(1)比较基础,学生都能掌握.对于问题(2),学生看完答案以后都有着同样的疑问:我怎么就能想到去计算FA→·FB→呢?难道靠猜测吗?如果猜测错误,怎么办呢?
资料提供的解答是通过计算得到 0,得∠AFB=90°,即∠AFB的大小为定值.这样的解答过程跳跃性很强,脱离学生的经验,未从学生的最近发展区出发,学生很难接受.为了易于学生理解,笔者在本例题第(2)问的讲解过程中进行了以下两种途径的尝试.
0,得∠AFB=90°,即∠AFB的大小为定值.这样的解答过程跳跃性很强,脱离学生的经验,未从学生的最近发展区出发,学生很难接受.为了易于学生理解,笔者在本例题第(2)问的讲解过程中进行了以下两种途径的尝试.
2途径尝试
2.1从特殊情况出发根据题意从特殊情况出发得出一个值(此值一般就是定值),然后证明定值,即将问题转化为证明待证式与参数(某些变量)无关.证法1①当直线l的斜率为0时,直线l的方
程为
 时,设直线x=3与x轴交于点E,如图1所示.
时,设直线x=3与x轴交于点E,如图1所示.
由勾股定理逆定理可得∠AFB=90°.
同理直线l的方程为y=-2时,∠AFB=90°.
②当直线l的斜率存在且不为0时,设直线l的方程为y=kx+m,直线x=3与x轴交于点E,如图2所示.以下同资料提供的解答.
综上,∠AFB的大小为定值.
点评处理问题(2)时,从直线l的斜率为0开始,此时的计算比较简单,通过计算得到所求角∠AFB=90°.这样给解答提供了方向,使得学生明白接下来只要证明当直线l的斜率存在且不为0时,能得到∠AFB=90°即可.可以通过计算FA→·FB→=0,得∠AFB=90°.也可以借助三角形相似证明.过点A作AH⊥x轴于点H,如图3所示.通过计算


Rt△AHF∽Rt△FEB,所以∠HFA=∠EBF,这样也可以得到∠AFB=90°.
2.2从问题结论出发将要证明的结论用动点坐标或动线中的参数表示,再利用其满足的约束条件使其绝对值相等的正负项抵消或分子、分母约分得定值.
 因为∠AFB∈(0°,180°),所以∠AFB=90°.点评解法2的思维非常简单,因为要证明∠AFB的大小为定值,所以只需要根据已知条件计算出cos∠AFB的值为定值即可.
因为∠AFB∈(0°,180°),所以∠AFB=90°.点评解法2的思维非常简单,因为要证明∠AFB的大小为定值,所以只需要根据已知条件计算出cos∠AFB的值为定值即可.
3结论拓展
已知椭圆
 设椭圆C的 右焦点为F,直线l与椭圆C相切于点A,与直线x=a2c相交于点B,则∠AFB的大小为90°.
设椭圆C的 右焦点为F,直线l与椭圆C相切于点A,与直线x=a2c相交于点B,则∠AFB的大小为90°.
4总结反思
4.1夯实基础知识
平时的教学要立足于课本,强化基础知识.教师应从教材的例题和习题中寻找试题的“根”,加强基础知识的复习,要列出具有典型性和代表性的题目进行讲解分析和训练,而且还要进行一题多变的训练.通过对题目的式子、图形、条件、结论、表达方式等的变化转换,促进学生触类旁通,巩固基础知识.
4.2强化通性通法
在数学教学中,重视通性通法的使用和理解,通过通性通法揭示问题的本质.只有真正重视通性通法教学,才能使得学生抓住数学问题的本质,学生的核心素养才能得到提高.如解法1中,从直线l的斜率为0时开始研究,这样便于学生理解.
4.3反思解题过程
在日常的教学中教师要指导学生如何进行反思,帮助学生养成反思的习惯.教师可以和学生一起回忆问题的解答过程,找出问题所在,帮助学生分析不能顺利答题的原因,提出改进方法.教师要带领学生立足已有的经验,从他们的最近发展区出发,思考有没有更简洁、更佳的解决问题的途径.学生在教师的带领反思中领悟方法,学会真正的反思,养成反思的好习惯.在反思中提升自我,提高解题效率.
参考文献:
[1]姬彩生.高考数学圆锥曲线解题技巧研究[J].数理化解题研究,2022(10):18-20.
[2]金家庆.探究高中数学解题思路以及解题能力的训练[J].数理化解题研究,2022(12):50-52.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/44603.html
 的离心率为
的离心率为 且椭圆C过点
且椭圆C过点

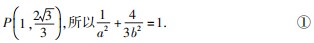
 ,所以
,所以 .②
.② ③
③



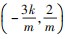 点B的坐标为(3,3k+m).因为右焦点F的坐标为(1,0),
点B的坐标为(3,3k+m).因为右焦点F的坐标为(1,0),

 0,得∠AFB=90°,即∠AFB的大小为定值.这样的解答过程跳跃性很强,脱离学生的经验,未从学生的最近发展区出发,学生很难接受.为了易于学生理解,笔者在本例题第(2)问的讲解过程中进行了以下两种途径的尝试.
0,得∠AFB=90°,即∠AFB的大小为定值.这样的解答过程跳跃性很强,脱离学生的经验,未从学生的最近发展区出发,学生很难接受.为了易于学生理解,笔者在本例题第(2)问的讲解过程中进行了以下两种途径的尝试.
 时,设直线x=3与x轴交于点E,如图1所示.
时,设直线x=3与x轴交于点E,如图1所示.
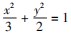 ,所以/BE/=
,所以/BE/= ,
,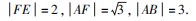


 Rt△AHF∽Rt△FEB,所以∠HFA=∠EBF,这样也可以得到∠AFB=90°.
Rt△AHF∽Rt△FEB,所以∠HFA=∠EBF,这样也可以得到∠AFB=90°.
 设椭圆C的 右焦点为F,直线l与椭圆C相切于点A,与直线x=a2c相交于点B,则∠AFB的大小为90°.
设椭圆C的 右焦点为F,直线l与椭圆C相切于点A,与直线x=a2c相交于点B,则∠AFB的大小为90°.