2022 年数学新高考Ⅰ卷第 16 题探究

 

SCI论文（www.lunwensci.com）：

　　摘  要 :文章以 2022 年新高考 Ⅰ 卷 16 题为例 ,探析直线与椭圆位置关系中涉及弦长问题的解
决途径 ,并基于此进行变式拓展.

　　关键词 : 高考试题;圆锥曲线;变式拓展
　
　　直线与 圆 锥 位 置 关 系 中 的 弦 长 问 题 是 解 析 几何的一种重要类型 , 由于这类问题常常涉及较 为繁 杂 的 计 算 , 较 多 出 现 在 高 考 的 解 答 题 中 , 2022 年新高考 Ⅰ 卷在客观题出现( 第 16 题) ,让 笔者眼前 一 亮 , 下 面 谈 谈 对 该 试 题 的 探 究 , 以 期 抛砖引玉.

　　1 题目呈现
　　题目  (2022 年新高考 Ⅰ卷第 16 题) 已知椭圆C :  +  = 1 ( a > b > 0) , C 的上顶点为 A ,两个焦 点为 F1 ,F2 ,离心率为  ,过点 F1  且垂直于 AF2 的直线与 C 交于 D ,E 两点 , | DE  ∣ = 6 ,则△ADE 的周 长是_____ .

　　本题以椭 圆 为 载 体 , 考 查 了 椭 圆 的 方 程 、直 线与椭圆的位置关系 、椭圆的定义以及椭圆中的 弦长等基 础 知 识 ; 考 查 了 空 间 想 象 、运 算 求 解 等 能力 ;考查函数与方程 、数形结合 、化归与转化等 思想 ;考查直观想象 、数学运算等核心素养 ;体现 基础性 、综合性.

　　2 解法分析

　　解法 1    因为椭圆离心率为 1

　　故设 C :  + = 1.
 

　　因为△AF1 F2  为正三角形 ,

　　则直线 DE 的斜率k =  .
 

　　由等腰三角形性质 ,得

　　AE  =  EF2    ,  AD  =  DF2   .

　　则△ADE 的周长等于 DE  +  DF2     +  EF2     =4a.

　　设直线 DE 的方程为 y = ( x + c ) ,
 

　　与椭圆方程联立 ,得 13x2  + 8cx - 32c2  = 0.

　　
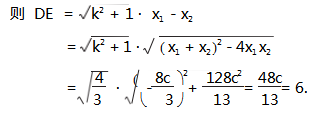
　　所以 c =  ,4a = 8c = 13.

　　所以△ADE 的周长是 13.

　　评析  先利用离心率得到椭圆的方程为+ = 1 ,根据图形的特征得到直线 DE 的斜率 ,写出直线 DE 的方程 ,再利用弦长公式求得 c 及 a 的值 , 再根据对称性将△ADE 的周长转化为△F2DE 的周 长 ,利用椭圆的定义求得周长.
 

　　解法 2  因为椭圆离心率为.

　　所以 a =2c,b = 3c.

　　则△AF1 F2 为正三角形 , ∠AF2 O =60° . 

　　显然直线 DE 是线段 AF2 的垂直平分线.

　　所以∠DF1 O = 30° .

　　由椭圆的极坐标方程 ρ =  ( 0 < e < 1) ,其中 e 是椭圆的离心率 ,p 是焦点到对应准线的距 离 ,θ 是弦与 x 轴所夹的角度.

　　故  DE  =  DF1  +  EF1

　　
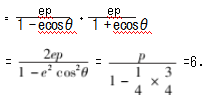
　　解得p = .
 

　　即- c =  =  .
 

　　又 b = 3c,代入得 c =  ,下同解法 1.

　　评析  本题的难点 是 求 弦 DE 的 长 度 ,发 现DE  =  DF1  +  EF1  ,利用圆锥曲线的极坐标方 程使得解法优化 ,其余解题思路同解法 1.

　　3 变式拓展

　　变式 1  已知椭圆 C :  +  = 1 ( a > b >0)的离心率为 过右焦点F 且倾斜角为 π  的直线与椭圆 C 相交的弦长为 ,且椭圆 C 上存在 4 个点 M,

N,P ,Q 构成矩形 ,则矩形 MNPQ 面积的最大值为______.

　　解析  由于


　　所以 a2 = c2 ,b2 = a2 - c2 =c2 .
 

　　故椭圆方程为 x2 +4y2 = c2 .
 

　　设过右焦点 F 的直线为 y = x - c,

　　与椭圆方程联立 ,得 5x2 - 8cx + c2 =0.
 

　　设直线与椭圆 C 的两交点为 (x1 ,y1 ) , ( x2 ,y2 ) ,则有 x1 + x2 =  ,x1x2 =  .
 

　　故 · 
  .

　　解得 c = 3. 则 a2 = c2 =4 ,b2 =c2 = 1.
 

　　所以椭圆方程为 + y2 = 1.

　　不妨设点 M 位于第一象限 ,坐标为 ( m,n) ,则 m2 + 4n2 = 4 ,矩形 MNPQ 面积为 2m ·2n = 4mn ≤ m2 +4n2 =4 ,当且仅当 m = 2n,即 m = 2 ,n =时 ,

等号成立.

　　故矩形MNPQ 面积最大值为 4.

　　变式 2  已知▱ABCD 的四个顶点均在双曲线x2 -  = 1 上 ,点 P(0 ,1 )在边 AB 上 ,且=  ,则▱ABCD 的面积等于______.
　

　　解析  由平行四边形的对称性与双曲线的对称 性 ,知点 O 为平行四边形的中心 ,A,B ,C ,D 四点在 两支双曲线上各有两点 ,不妨设点 A,D 在左支上 , 点 B ,C 在右支上 ,如图 1 ,考虑点 A,B 关于双曲线 中心的对称点 A′ ,B′ ,因为单支双曲线上不存在四 点构成平行四边形 ,知 A′ = C ,B′ = D,所以▱ABCD 的对称中心为 O.
 

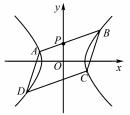
图1
 

　　设 A( x0 ,y0 ) ,由= ,得 B ( -2x0 ,3 -2y0 ).
 

　　将点 A,B 的坐标代入双曲线方程 ,得

　　

　　变式 3  抛物线 C :x = 2py2 (p > 0) 的焦点 F 到 准线的距离为2 ,过点 F 的直线与 C 交于A,B 两点 , C 的准线与 x 轴的交点为 M,若△MAB 的面积为3 2 ,则 = _____.
 

　　解析  抛物线 C :x =2py2 (p > 0)化为标准形式为 y2 = x(p >0).
 

　　因为抛物线的焦点 F 到准线的距离为 2 ,

　　所以 =2 ,即 p = .

　　则抛物线方程为 y2 =4x(p >0) ,焦点 F( 1 ,0 ).

　　设直线 AB 方程为 x = my + 1 ,

　　与抛物线方程联立 ,得 y2 -4my -4 =0.

　　设 A( x1 ,y1 ) ,B ( x2 ,y2 ) ,不妨假设点 A 在 x 轴上 方 ,点 B 在 x 轴下方.

　　则 y1 + y2 =4m,y1y2 = -4.

　　

　　设点 M 到直线 AB 的距离为 d,则

　　

　　所以 S △MAB =AB ·d
 

　　=  1  × 4 ( 1 + m2 ) ×  

　　
　　解得 m2 =， 则 m = ± .
 

　　当 m =时 ,y1 + y2 = 2,y1y2 = -4 ,
 

　　

　　所以 AF= x1 + 1 = 3 , BF = x2 + 1 =  . 则=2.
 

　　

　　则 =  . 故答案为 2 或.
 

　　参考文献 :

　　[1] 蔡海涛. 几类直线与圆锥曲线位置关系 问题 [J]. 高中数学教与学 ,2019(08) :38 -41.