SCI论文(www.lunwensci.com)
摘要:“人本智造”已成为智能制造的新研究方向,日常生产活动需要更多考虑人类工效学(Ergonomics)。目前装配生产线平衡优化主要以提高装配效率为目的,缺乏对装配过程中人类工效学的关注。给出职业重复动作(OCRA)方法详细计算过程,并基于OCRA方法从动作频率、尴尬姿势、体力消耗及额外风险等方面对装配过程的人因风险进行评估,考虑不同作业元素优先关系约束、工作站节拍约束、任务关联性约束和操作者人因风险约束等约束条件,以最小化工作站数为优化目标,建立考虑人因风险的Type-Ι装配线平衡优化模型,进而采用改进的遗传算法作为求解算法,在初始化种群阶段基于优先级规则初始化种群,以提高收敛速度。通过对比算例分析结果,表明提出的模型合理且算法有效。
关键词:装配线平衡;人因风险;遗传算法
An Assembly Line Balancing Optimization Method Considering Human Factor Risk
Qin Peihua,Lin Libin,Zhang Ding
(School of Electromechanical Engineering,Guangdong University of Technology,Guangzhou 510006,China)
Abstract:Human-centered intelligent manufacturing has become a new research direction for smart manufacturing,and daily production activities need to take Ergonomics more into account.The current balancing optimization for assembly lines is mainly aimed at improving assembly efficiency,and still lacks attention to human ergonomics in the assembly process.The detailed calculation process of the occupational repetitive action(OCRA)method is introduced,and the human factor risk of the assembly process based on the OCRA method in terms of action frequency,awkward posture,physical exertion and additional risk is evaluated,constraints such as priority relationship constraints for different operational elements,workstation beat constraints,task relevance constraints and operator human factor risk constraints are considered,and take minimizing the number of workstations as the optimization.The Type-Ιassembly line balancing optimization model considering human factor risk is established as the objective,and then an improved genetic algorithm is used as the solution algorithm,and priority-based rules are used to initialize the population in the initialization phase to improve the convergence speed.By comparing the results of the algorithm,it is shown that the model proposed is reasonable and the algorithm is effective.
Key words:assembly line balancing;human factor risk;genetic algorithm
0引言
“人本智造”就是将以人为本的理念贯穿于智能制造系统的全生命周期过程[1]。我国仍是劳动密集型制造大国,据统计,全球约80%的个人计算机、65%的智能移动电话和彩电均在国内装配生产。目前OEM企业装配线生产规划活动中,较少考虑人因工程的影响,仍是粗狂式安排作业任务。在“机器代人”趋势下,引入了非标自动化代替手工作业(如移动电话装配代工厂),人和机器的合理配合愈加重要。
装配线平衡能够有效提高生产效率、降低库存成本以及提高产品质量,实现企业的可持续发展。目前国内大多数制造业就如何提高装配线的平衡率进行了大量研究,但对降低制造过程中技术工人的作业负荷缺乏关注。随着中国制造2025的持续深入以及工业5.0的提出,"人本智造"、工人福祉和可持续发展成为关注的重点[2-4]。在工业5.0时代,企业考虑装配过程中人因风险,贯彻以人为本的智能制造理念,对推动企业创新发展具有重要意义。
Boysen等[5]针对装配线平衡目标的不同,进一步将装配线平衡问题分为3类。(1)SALBP-1:生产节拍固定,最小化工作站的数量;(2)SALBP-2:在工作站数量确定的前提下,最小化作业节拍时间;(3)SALBP-E:工作站数量和预设节拍均给定,求可行解。闫琼等[6]针对SALBP-1提出了一种改进的差分进化算法并验证了算法的有效性。高振豪等[7]结合成组技术、遗传算法建立数学模型求解SALBP-2。
WEI等[8]制定了SALBP-E模型并最大限度地提高了装配线平衡效率,并最大限度地减少了闲置时间。后续国内外学者针不同的目标和约束条件对线平衡优化问题进行优化。黄玉开等[9]针对混合装配线以均衡工作站负荷和最小化制造周期为目标,建立平衡与排序数学模型,并采用遗传算法求解。尹胜利[10]通过Flexsim针对装配线流程以及相应工序操作时间和人数等参数进行仿真,发现瓶颈工序,并运用ECRS原则来提高装配线平衡率。焦玉玲等[11]提出混流排序和平行双边装配线平衡联合优化方法,采用多级约束的启发式算法以减少混流平行双边装配线工作站数量。杜利珍等[12]采用自适应增长的权重更新策略,将模拟退火算法和果蝇算法结合,提高了果蝇算法的全局搜索性,以解决空调外机装配线平衡问题。郑晨昱等[13]针对人机协作装配线平衡问题,构建了混合整数规划模型实现小规模案例求解,同时提出改进人工蜂群算法实现大规模问题求解。
在实际装配过程中,人类工效学往往不可忽视。降低人类工效学风险(又称“人因风险”)可以保障工人作业时的健康和舒适,提高工人工作满意度,保证装配生产效率和产品质量[14]。目前在人类工效学方面理论和研究,已经构建了一个相对完整的理论体系。针对不同的作业场景,提出了多个人因风险的评估方法[15],包括OCRA(Occupa⁃tional Repetitive Actions)、OWAS(Ovako Working Posture Analysis System)、REBA(Rapid Entire Body Assessment)、NIOSH(National Institute for Occupational Safety and Health Method)和EAWS(European Assembly Worksheet)等。
尽管人类工效学的理论相对完善,但目前基于人因风险的装配线平衡优化问题仍然考虑不多。Ozdemir等[16]采用了模糊集理论建立一个考虑人类工效学风险的装配线设计模型,并应用在某冰箱企业的装配线案例中。E Stecke等[17]建立了混合整数线性规划模型、约束规划模型和Benders分解算法,并采用能量消耗法来评估人类工效学风险,优化人机协作装配线的周期时间和人类工效学风险。Mura等[18]考虑频繁执行重复动作和搬运重型部件的装配场景,提出了一种基于能量消耗的考虑人类工效学风险的多目标遗传算法来解决装配线平衡问题。Otto等[19]分析了OCRA、NIOSH、EWAS来建立人类工效学装配线平衡模型,并基于模拟退火提出了一个两阶段启发式方法,在不增加工作站和工人数量的前提下显著降低技术工人的人因风险。Jaturanonda等[20]采用RULA方法对工人的姿势负荷进行评估,以改进装配线初始任务工作站分配解决方案。从长远看,在装配线上考虑人因风险,对提高装配效率和降低生产成本具有指导性意义。
本文基于OCRA方法来评估装配线的人因风险,以手工作业的装配线为研究对象,建立满足多个约束的考虑人因风险的装配线平衡模型,提出一个基于优先级规则的改进遗传算法。最后通过某装配线实例验本文所提机制的有效性。
1考虑人因风险的装配线平衡问题模型
1.1人因风险评价方式
作业人因风险指的是在工作中,由于工作本身的性质、工作环境、工作组织和管理等方面的因素,导致工人受到的健康和安全风险。这些因素可能包括机器设备的不安全操作、工作场所的不安全环境、工作强度和时间的过度压力等。作业人因风险可能对工人的健康和安全造成威胁,导致工伤和职业病的发生,甚至可能导致生命危险。
OCRA方法是一种用于评估重复性动作的人类工效学方法。OCRA方法主要分析评估工人在生产线上进行重复性动作时所承受的风险。一般来说,OCRA指数考虑上肢完成的任务,并对每只手分别进行人类工效学分析。通过评估内容包括作业任务中的姿势、力量、重复性和附加风险等,计算出OCRA指数来评估工作任务对技术工人的肌肉骨骼系统和人体负荷水平,为改进工作环境和降低工作风险提供科学依据。
1.2基于OCRA人因风险值计算
欧洲标准CEN对OCRA指数作出了等级划分,建议将OCRA小于2.3的风险等级视为可接受(绿色),2.3~3.6之间的风险等级为不确定(黄色),而OCRA指数在3.6之上的视为不可接受(红色)。其风险等级划分如表1所示。
图1是一个考虑OCRA指数的工作站分配例子,在没有考虑人因风险的情况下两个分配方案均满足生产条件,然而分配方案(a)中工作站1的OCRA指数为3.03;考虑OCRA指数的情况下对装配线重新平衡,得出方案(b),各工作站的人因风险均在合理的范围之内。
1.3一个OCRA风险值计算例子
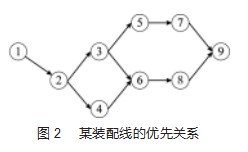
为了更好地理解该问题,下面将提供一个说明性示例。某装配线的作业元素n=9,装配任务优先关系如图2所示,该装配线工作站数M=3,该工作站的分配情况如表4所示。
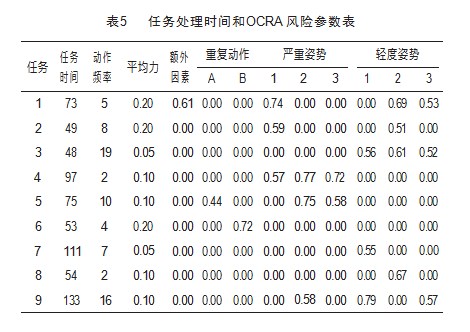
另外,该装配线各任务处理时间和OCRA风险参数已知。表5展示了各个OCRA风险值的各个参数详细数据。
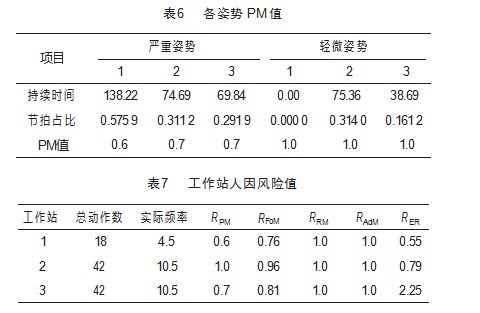
在该装配线案例中,工作站的总处理时间分别为219、234和240,因此节拍时间为240,根据式(1),通过OCRA方法计算得到的各工作站的人因风险值分别为0.55,0.788和2.252。具体以工作站1为例,有3个任务1、2和4,对应的加工时间分别73、49、97。可得这些任务的技术动作数(向上取整)为7、7和4。因此,工作站1的实际频率为4.5。工作站1的严重姿势1的持续时间为138.22 s,占节拍的57.59%,查表2得其对应的PM值为0.6,同理其余姿势的PM值如表6所示。每个工作站取其最小的值作为工作站的姿势乘数,工作站1的姿势乘数被设置为0.6。此外,工作站1的平均力度等级为14.29%,查表3并使用内插法计算的FoM值为0.76。两种重复动作的持续时间均为0,周期时间CT超过15 s,因此RRM=1.0。附加因素的持续时间为44.53 s,占循环时间的18.60%,因此AdM值为1.0。工作站1的OCRA风险指数IER1为0.55。采用相同的OCRA方法,计算工作站2和工作站3人因风险值如表7所示。
2考虑人因风险的装配线平衡优化问题建模
2.1问题描述
该问题属于考虑人因风险的第一类装配线问题,该问题可以描述成在给定节拍CT和作业元素N以及每个作业元素对应的作业时间t的情况下最小化工作站数量M和人因风险值IERm。在建立相关模型之前,做出如下假设:(1)该线为单一品种单边装配线,单次平衡只装配一种产品;(2)该线的节拍时间已知;(3)忽略其他扰动因素对作业时间产生的影响,每个作业元素的作业时间固定;
(4)作业元素的加工顺序必须满足作业优先关系;
(5)每个作业元素为最小作业单元,无法进行分割分配到两个工作站。
2.2参数定义和数学模型
考虑人因风险的装配线平衡优化问题涉及的参数及符号定义如表8所示。
式(6)约束确保每个作业元素都被分配到某个工作站且仅分配其中一个工作站;式(7)约束保证所有的作业元素分配满足作业优先关系;式(8)约束保证各个工作站的累计作业时间不能超过节拍时间;式(9)约束保证具有关联关系的作业元素(兼容任务)分配到同一个工作站;式(10)约束保证不兼容的作业元素(不兼容任务)不被分配到同一工作站;式(11)为人因风险值约束,保证每个站点的人因风险不超过一个设定的值,当K设定为2.3,全部工作站的人因风险等级为可接受的。
3算法设计
该装配线问题随着作业元素和工作站数的增多,可行解的数量呈指数型增长。传统遗传算法(Genetic Algorithm,GA)在求解此类NP-Hard问题的时候具有良好的效果,但算法在求解过程中精度不高,且容易陷入局部收敛。针对传统遗传算法的不足,本文对它作出了改进。
3.1编码
本文采用整数编码的染色体编码方式,染色体上每一个基因位代表一个工序。染色体的总基因数与作业元素数量总和相同,保证每一个基因在该染色体上只表达一次。产生的基因序列即为一条经过编码的染色体。
具体编码方法为随机选取作业优先关系矩阵中列元素全部为0的作为当前编码位,随后将被选中作业元素所在行元素全部置0。重复上述操作直至分配完成。
3.2解码
解码采用的是面向站点的向前解码。即按照染色体的基因顺序,运用贪心算法将对应作业元素分配到工作站中。若工作站累计的实际作业时间超过给定节拍,则工作站编号加1,将该元素移到下一个工作站。
3.3初始化种群
为了提高算法的收敛速度,区别于完全随机生成初始化种群,本文对初始化种群的机制进行了改进。在不考虑每个工作站人因风险约束的情况下,SALBP-1问题的模型为线性混合整数规划模型,可采用CPLEX求解器实现小规模案例的精确求解。而人因风险值的计算并不是线性的,并不能作为约束加入问题模型进行求解。针对小规模案例,本文第一阶段求解过程不考虑人因工程学风险条件约束,使用CPLEX求解器进行精确求解,得到一个基于优先级规则构造的初始解。第二阶段将第一阶段产生的初始解作为GA的初始种群,数量为初始种群数量的一半,并与随机产生数量也为初始种群规模一半的初始解组成最终的初始种群。提高算法收敛速度的同时避免该初始种群丧失种群的多样性。
3.4适应度评价
适应度函数是用来评价种群个体好坏的标准。本文属于第一类装配线平衡问题,建立的数学模型的目标函数为最小化工作站数量m。但以m作为评价函数会导致搜索过程改进缓慢且随机性高,因此采用每个工作站m的加工时间的平方和作为适应度评价函数,保证在遗传迭代的过程中能够持续改进。适应度函数如式(12)所示。
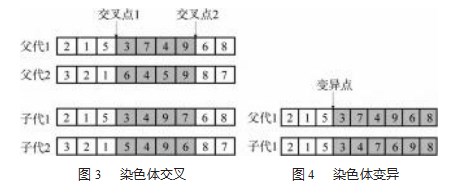
由于该问题存在作业优先关系约束,单一交叉会产生不可行解。为了避免产生不可行解,保证交叉后得到的新染色体均为合法解,本文选择双点交叉法。随机生成两个交叉节点,将两条父代染色体均分成三段,父代染色体1和父代染色体2两个交叉点外的基因片段分别直接进入子代1和子代2染色体。由于两个父代染色体内的基因序列均满足作业优先关系约束,搜索父代1染色体中两个交叉点间的基因在父代2中的排列顺序,以此作为子代1两个交叉点中的基因片段;同理可得子代2两个交叉点中的基因片段。如图3所示。
(3)变异
变异能够避免搜索过程过早陷入局部最优,保证种群的多样性。根据设定的变异概率选择变异的染色体,并在变异的染色体上随机产生一个变异节点将染色体分为两段。父代的前半段染色体保持不变直接进入子代,后半段染色体按照作业优先顺序重新排列,完成变异操作。如图4所示。
4案例分析
为了验证模型和算法的有效性,本文针对上述问题基于公开的数据集生成了一组基准实例。这些公开的基准测试实例可以在https://assembly-line-balancing.de/下载。本文选取了其中的mertens7,bowman8,jaeschke9,jackson11,mansoor11,mitchell21,roszieg25,heski⁃aoff28,buxey29,sawyer30,lutz32和gunther35作为小规模案例。实验是在配备2.80 GHz Intel(R)Core(TM)i5-10400F处理器和32 GB RAM的Windows 10 Profession⁃al PC上进行的。此外,算法设置的初始种群大小为200,交叉概率为0.8,变异概率为0.1,迭代次数为600。
表9所示为本文选取的其中一个说明案例sawyer30_c=25_iteration1,该案例给定的节拍时间CT=25 s,有30个作业元素且每个作业元素的各个人因风险参数值已知。不考虑人因的情况下求得到最小工作站数为14,改进遗传算法求得的结果和目前已知的最好结果相同,表明了改进遗传算法的有效性。然而不考虑人因风险约束,该工作站任务分配方案虽然能满足节拍要求,但工作站2的人因风险值却超过了2.3,会对在该工作站上作业的工人带来健康损害。现阶段考虑人因风险对装配线平衡问题优化求解,得到表9右侧的方案,同样的该方案能够在满足装配最少工作站的同时保证作业工人的负荷均衡。
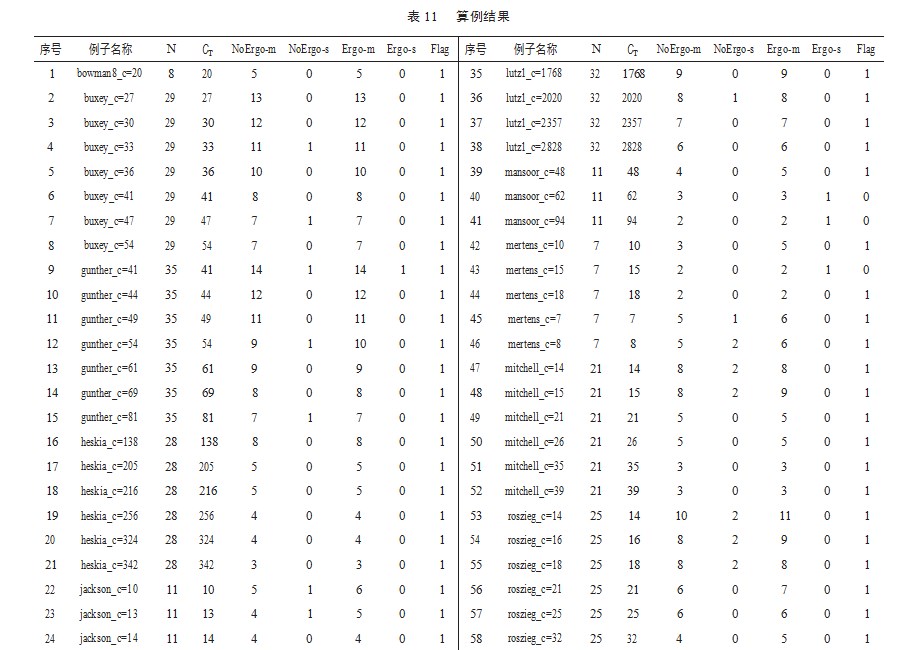
此外为了进一步验证模型的有效性,本文还选取上述生成的公开测试集对模型进行求解测试,记录每个测试实例中不考虑人因风险时的最少站点数量、人因风险值超载站点数量以及考虑人因风险约束后的最少站点数量和人因风险值超载站点数量。随后记录测试结果,判断改善后方案是否满足人因风险。符号说明如表10所示,表11所示为测试结果。
算例结果显示在不考虑人因风险情况下所有实例均可求得最小的工作站数量,但此时存在部分工作站OCRA值较高。考虑人因风险约束后对装配线进行优化,不满足产线装配人因风险的情况明显减少。尽管考虑人因风险约束之后个别装配线的工作站总数增多,但降低了人因风险超载站点数量,是降低生产成本、提升产品质量最经济有效的方式,符合实际生产需求。特别地,个别作业元素受限于该工序本身人因风险值较高以及作业优先关系原因,其所在工作站并不能满足人因风险要求,需要企业根据实际生产情况重新考虑工艺流程。
5结束语
对于手工化程度较高的装配线,装配过程的人类工效学风险不可忽视。本文针对第一类装配线平衡问题,考虑装配过程的人类工效学问题,提出采用OCRA方法评估装配线的人因风险等级。针对该考虑人因风险的装配线平衡优化问题,建立了满足多个约束的装配线平衡模型,满足人因风险评估的同时最小化工作站数量;设计了改进的遗传算法,提高收敛速度的同时增加种群多样性;并通过公开测试集对装配线模型和算法进行了分析和验证。实例表明,该方法能够有效降低装配线的人因风险指数,提高装配线的生产效率,为企业解决该类问题提供新思路。
参考文献:
[1]Wei H,Zhijun L,Philip L C C.A survey of human-centered intel⁃ligent robots:issues and challenges[J].IEEE/CAA Journal of Au⁃tomatica Sinica,2017,4(4):602-609.
[2]周济.智能制造——"中国制造2025"的主攻方向[J].中国机械工程,2015,26(17):2273-2284.
[3]Nahavandi S.Industry 5.0—A human-centric solution[J].Sustain⁃ability,2019,11(16):4371.
[4]Leng J,Sha W,Wang B,et al.Industry 5.0:Prospect and retrospect[J].Journal of Manufacturing Systems,2022,65:279-295.
[5]闫琼,张海军,张国辉,等.基于改进差分进化算法的多目标第Ⅰ类装配线平衡问题研究[J].科技通报,2017,33(11):197-200.
[6]高振豪,苏贵影,余燕尾.基于成组技术的遗传算法求解第Ⅱ类装配线平衡问题[J].物流科技,2017,40(6):61-65.
[7]Wei N C,Chao I M.A solution procedure for type E simple as⁃sembly line balancing problem[J].Computers&Industrial Engi⁃neering,2011,61(3):824-830.
[8]Boysen N,Fliedner M,Scholl A.A classification of assembly line balancing problems[J].European journal of operational research,2007,183(2):674-693.
[9]黄玉开,唐秋华,梁燕丽.基于遗传算法的混装线平衡与排序研究[J].机电工程技术,2011,40(5):36-39,73,124.
[10]尹胜利.基于Flexsim的净水控制器装配线平衡仿真与优化[J].机电工程技术,2022,51(7):192-195.
[11]焦玉玲,邓雪,李津,等.混流平行双边装配线平衡建模与启发式算法[J].计算机集成制造系统:1-14[2023-03-22].
[12]杜利珍,张亚军,董理,等.基于改进果蝇算法的第一类装配线平衡率优化[J].组合机床与自动化加工技术,2023,(1):184-187,192.
[13]郑晨昱,李梓响,唐秋华,等.基于改进人工蜂群算法的人机协作装配线平衡优化[J].计算机集成制造系统:1-17[2023-03-22].[14]Bridger R.Introduction to ergonomics[M].CRC Press,2008.
[15]Lowe B D,Dempsey P G,Jones E M.Ergonomics assessment methods used by ergonomics professionals[J].Applied ergonom⁃ics,2019,81:102882.
[16]Ozdemir R,Sarigol I,AlMutairi S,et al.Fuzzy multi-objective model for assembly line balancing with ergonomic risks consid⁃eration[J].International Journal of Production Economics,2021,239:108188.
[17]Stecke K E,Mokhtarzadeh M.Balancing collaborative humanro⁃bot assembly lines to optimise cycle time and ergonomic risk[J].International Journal of Production Research,2022,60(1):25-47.[18]Dalle Mura M,Dini G.Optimizing ergonomics in assembly lines:A multi objective genetic algorithm[J].CIRP Journal of Manufac⁃turing Science and Technology,2019,27:31-45.
[19]Otto A,Scholl A.Incorporating ergonomic risks into assembly line balancing[J].European Journal of Operational Research,2011,212(2):277-286.
[20]Jaturanonda C,Nanthavanij S,Das S K.Heuristic procedure for the assembly line balancing problem with postural load smoothness[J].International journal of occupational safety and rgonomics,2013,19(4):531-541.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/77466.html