基于神经网络和遗传算法的 BK7玻璃精密模压成形多目标优化论文

SCI论文（www.lunwensci.com）

　　摘要 ：残余应力和形貌偏差是玻璃模压成形影响整体质量的重要指标， 而影响这些指标的成型条件是一个多因素问题 。为了得到 玻璃精密模压成形过程中成形透镜的残余应力和形貌偏差的极小值， 以模压成形工艺参数为决策对象， 以玻璃透镜产品质量为优 化目标， 对成形工艺参数进行多目标优化分析， 优选出最终结果 。首先基于仿真与实验结合对玻璃成形过程进行分析验证， 然后 采用正交实验方法选择合理参数， 用有限元技术得到模压成形透镜实验样本的最大残余应力 、成形应力 、最大形貌偏差， 并使用 方差统计分析方法降维筛选出主要成分， 建立合理的分析主参数， 接着利用人工神经网络映射成形工艺参数与优化目标间的关系， 建立工艺优化的数学模型， 最后利用遗传算法寻找最优解 。结果表明提出的基于人工神经网络和遗传算法的 BK7玻璃精密模压成 形工艺优化方法是有效可靠的。

　　关键词 ：BK7玻璃,模压成形,人工神经网络,遗传算法,有限元技术


　　Abstract: Residualstress and profile deviation are the key indexes for the quality of molded lens in the precision glass molding process . And the processing conditions affecting the forming quality is the multi factor problem . In order to require the minimum of the residual stress and deviation of molded lens during the BK7 glass precision molding process, a multi-objective optimization was proposed to optimize the glass molding process. The design variables were process parameters during the glass molding and optimization goals were the quality of molded lens . Firstly, the glass molding process were simulated and validated by combining the simulation and experiments . Then, the maximum residual, forming stress and maximum deviation of molded lens of the training sample were obtained from the orthogonal design and the finite element simulation. The statistical analysis of variance was used to select the main element and establish the suitable feedback parameters . Furthermore, a BP neural network model was map the relationship between process condition and optimization goals and established the optimization model of mathematics. Finally, a genetic algorithm was used to find the optimal solution. The results show that the combining the artificial neural network and genetic algorithm method is an effective and useful tool for the process optimization of BK7 glass molding.

　　Key words: BK7 glass; molding; neural network; genetic algorithm; finite element


　　0 引言

　　光学玻璃模压技术从 20 世纪 80 年代开始兴起， 是利 用高精密模具以及专门模压设备将接近软化的光学玻璃 一次性加工成所需要的光学元件， 广泛用于摄像机 、数 码相机 、手机 、投影仪 、CD 机 、红外探测仪等光电产品 中 。采用该技术可以直接热压成形精密的非球面光学元 件[1] 、光学衍射元件[2] 、光学微阵列元件[3] 、光栅[4]等， 给光电行业在光学玻璃加工上带来了新的变化和发展。

　　玻璃精密模压成形是在高温下产生形变， 由于冷却 阶段不均匀的温度场等因素， 导致最后残余应力仍留在 透镜内， 从而影响成形透镜的光学性能以及服役寿命 。 周天丰等[5]建立了改进的模具玻璃界面的摩擦模型， 对界面间滑移现象进行分析， 并得到微槽阵列的应力分布 图 。Yi 等[6]利用低熔点玻璃 K-PG325 模压成形了衍射光 学元件， 用高度 6.03 mm 直径 24 mm 的 BK7 玻璃圆片模 压成形出非球面透镜， 并对成形过程进行仿真分析， 得 到残余应力分布以及形貌偏差 。Sarhadi 等[7] 利用玻璃圆 环压缩试验验证了 Sandwich 模型的可靠性， 并通过仿真 对三维晶片的最终尺寸和残余应力进行评估分析。

　　冷却阶段， 玻璃尺寸收缩 、温度不均， 热压成形的 透镜存在折射率变化和形貌偏差的问题， 从而影响玻璃 透镜的光学质量 。Su 等[8]为了修正形貌偏差和折射率变 化， 提出了一种通过结合仿真结果修改模具尺寸的方法 综合补偿透镜的形貌偏差与折射率变化 。Puneet 等[9]分别对等温模压成形和非等温成形的非球面透镜的形貌偏差 进行仿真分析， 为了减小偏差值， 经过数次迭代计算可 以明显地减小形貌偏差 。Vu等[10]在非等温模压成形透镜 优化中， 运用了神经网络与遗传算法对成形工艺进行优 化， 优化后的玻璃形状偏差有所减小。

　　基于神经网络和遗传算法寻优计算， 寻优结果较为 合理， Shen 等[11]针对注塑成型工艺特点， 为了提高产品 的性能质量， 利用人工神经网络和遗传算法去优化成型 工艺参数， 结果表明了基于神经网络技术和遗传算法的 注 塑 成 型 工 艺 优 化 方 法 是 一 个 有 效 的 工 具 。 Shi[12]和 Hsueh-Lin[13]在后续对注塑成型工艺优化分析中， 同样采 用了人工神经网络和遗传算法， 证实了该方法的有效性 和可靠性 。 由于神经网络和遗传算法的优异性质， 已被 广泛应用到合金成分分析[14] 、铝合金压铸[15] 、食品冷冻 加工[16] 、 自适应控制和信号处理[17]等领域。

　　从以上研究成果可以看出， 不少学者针对玻璃精密 模压成形过程进行了分析， 通过有限元软件对成形透镜 的残余应力和形貌偏差进行预测， 并利用相应的计算方 法对透镜质量进行优化分析 。而实际生产中， 玻璃精密 模压成形是复杂的系统， 传统工艺参数选择一般通过试 错法及个人经验去获取最佳工艺组合， 不利于产品开发 周期 。随着数值模拟技术以及计算机软硬件的日益成熟， 利用有限元技术去预测产品的成形质量等技术指标和科 学的计算方法去优化工艺方案非常有必要。

　　本文首先利用正交实验设计方法和有限元技术结合， 对 BK7透镜模压成形工艺参数进行分析， 研究不同工艺 参数与成形透镜间的质量规律， 选取多个决策变量， 以 玻璃透镜的最大残余残余应力和最大形貌偏差为优化目 标， 构建模压成形工艺多目标优化数学模型， 利用遗传 算法对优化数学模型进行求最优解， 从而达到减小透镜 的残余应力与形貌偏差。

　　1 玻璃模压成形多目标优化流程

　　玻璃模压成形过程中， 各个工艺参数对成形透镜 的残余应力与形貌偏差的影响呈非线性， 且各参数间存在复杂的耦合关系 。影响玻璃模压成形的工艺参数 主要有模具温度 Tm 、保温时间 ts 、模压压力 Pm 、加压 时间 tm 、保压压力 Pk 、慢冷时间 Ct 、快冷时间 St 、加 热时间 Th 作为控制因子 。基于有限元软件建立玻璃精 密模压成形的有限元模型， 利用正交实验方法指导仿 真过程， 并实验验证仿真的可靠性 。接着将仿真结果 作为神经网络预测模型样本数据， 构建优化目标 (最 大残余应力 Sm 、最大形貌偏差 Dm ) 与决策变量 (工艺 参数) 之间的映射函数关系， 用遗传算法对参数进行 优化， 得到最优工艺参数组合， 其多目标优化方法路 线如图 1 所示 。


　　2 有限元模型的建立及仿真

　　2.1 有限元模型初始化

　　BK7 玻璃材料特性[20]如表 1 所示， 用于热压仿真实 验 。成形工艺参数取值范围如表 2所示， 作为优化数学 模型的约束条件。


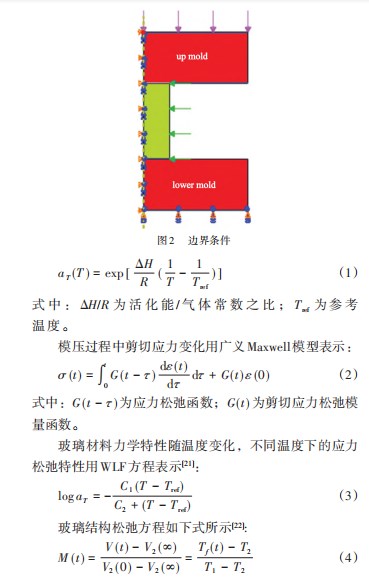
　　仿真模型为二维粘弹性轴对称模型， 其边界载荷条 件如图 2所示， 玻璃圆柱的热能大部分来自模具的热传 导 2 500 W/m ·2K， 小部分来自氮气对流 20 W/m ·2K。

　　在热压阶段， 分别分析黏弹性模型中应力松弛特性 和结构松弛特性存在的差异 。玻璃材料的热流变模型采 用 Arrhenius公式：


　　2.2 误差模型建立

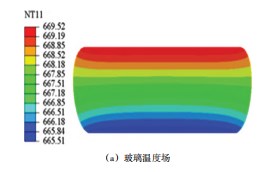
　　如图 3 所示， 模具加热至一定温度保温一定时间， BK7 玻璃温度场和应力场如 3 (a) 和 3 (b) 所示， 冷却 至室温玻璃内部温度场和残余应力如图 3 (c) 和 3 (d) 所示 。根据仿真的工艺参数， 利用玻璃精密模压设备进 行模压实验， 热压前后玻璃尺寸变化如图 4 所示 。不难 推测出， 不同的工艺参数对玻璃的内应力分布以及形貌 有很大的影响。


　　2.3 模压参数确定

　　利用有限元仿真软件 ABAQUS 对模压过程进行分析， 设定合适参数， 软件自动精确划分网格进行模拟 。 热压仿真过程如图 5所示， 模型为热力耦合模型和热位 移耦合模型。


　　双凸玻璃透镜模压成形主要包括： 加热 、保温 、热 压 、保压退火 、快冷脱模这几个阶段 。首先把模压腔室 里的空气抽空， 充入少量氮气防氧化， 接着用红外加热 装置将玻璃毛坯和模具加热到模压温度， 恒温一定时间 让玻璃受热均匀， 然后施加压力合模， 将玻璃模压成形， 保持压力一段时间， 充入少量氮气慢速冷却至 500 ℃， 接着充入大量氮气快速冷却室温， 最后脱模取样。

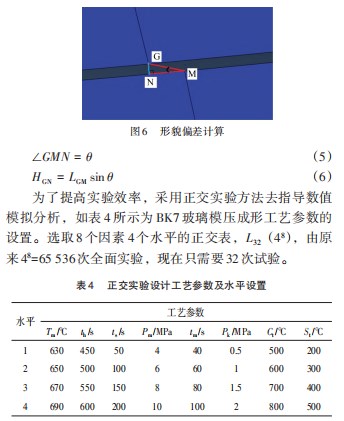
　　其中， 热压温度 、模压力 、模压速率 、冷却速率等 工艺参数对成形透镜的残余应力和形貌偏差有着较大的 影响 。如图 6所示， 通过获取室温下模具与透镜的坐标 信息， 然后计算得到透镜的形貌偏差。


　　3 实验样本数据的处理及正交分析

　　3.1 实验样本数据的获取

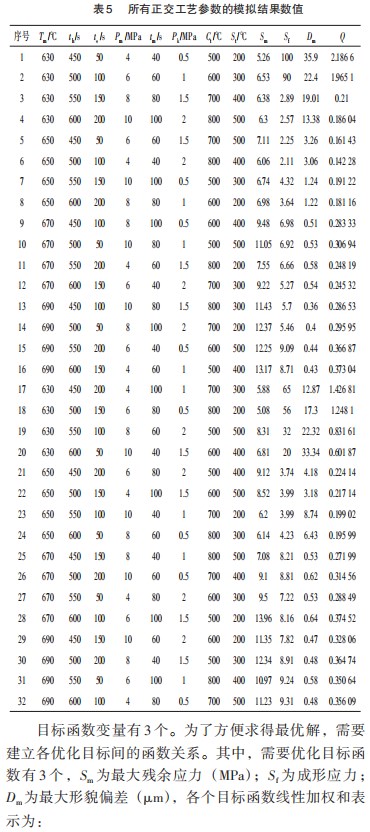
　　根据实验研究与模拟仿真结果， 选定需要优化的工 艺参数 ( Tm ,th ,ts ,Pm ,tm ,Pk , Ct ,St )， 采用正交实验方法进行实验设计 L32-4-9. 实验样本结果如表 5 所示， 样本 具备均匀分布的特点。


　　3.2 正交实验结果数据分析

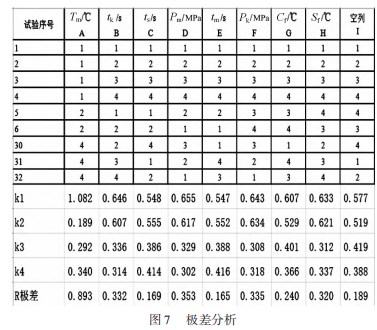
　　首先将正交试验获得的数据进行极差分析， 结果如 图 7 所示， 本研究最终目的是找出综合评价的 Q值的最 小值， 所以取各因素的 4 个水平值的平均数 (k值) 中最 小的那一个就是理想的最佳水平值 。按照这种逻辑， 各 因素的理想的最佳水平值就是： A2=650; B4=600; C3= 150; D4=10; E3=80; F3=1.5; G4=800; H3=400 。而从 32 组数据中， 可以直观搜索到最小的 Q值是第 6 组实验， Q=0. 142 28. 其对应的各因素的水平值是： A2=650; B2 =500; C2= 100; D1=4; E1=40; F4=2; G4=800; H3= 400 。理想最佳和实验最佳相比较， 发现只有 A2 、G4、 H3 三个因素相同， 未达到本研究的预期效果 。另外从极 差分析中可以看出各因素对最终评价值 Q 的影响的大小 为： A > D > F > B > H > G > C > E。


　　接着对相关数据在 SPSS 软件中进行方差分析， 得出 的结果如图 8 所示， 结果显示的各因素的显著性与极差 分析是符合的， 从具体的数据看， C /E /G 三个因素无统计学意义， 是可以忽略的因素 。其他 5 个因素的显著性 A > D = F > B = H。


　　根据以上两项分析， 决定采用神经网络的方法， 建 立数据量更多， 更全面的数据模型， 使用遗传算法求出 各因素的最佳参数。

　　4 神经网络模型建立及遗传算法优化

　　4.1 神经网络模型

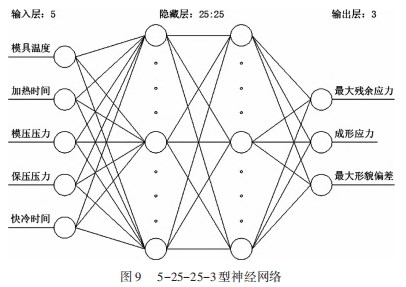
　　在电子科学 、计算机科学 、控制科学等实际应用中 大部分采用 BP 神经网络[18- 19] 。图 9 所示为构建的神经网 络模型结构示意图， 根据极差分析和方差分析的结果， 只采用具有统计学意义的 5 个因素放入分析模型， 即输 入层 5 个神经元， 代表的各个工艺参数是： 模具温度 Tm 、加热时间 th 、模压压力 Pm 、保压压力 Pk 、快冷时间 St， 中间层有两组神经元， 每组 25 个， 映射输入层与输 出层之间的关系， 输出层为优化目标： 最大残余应力 Sm 、成形应力 Sf 、最大形貌偏差 Dm， 神经网络结构为 8-25-25-3 型。


　　以模压成形玻璃透镜的残余应力 、成形应力和形貌 偏差为优化目标， 成形工艺参数： 模具温度 、模压力、 保压力 、快冷时间 、加热时间为决策变量， 优化数学模 型如下式所示：


　　4.2 遗传算法优化

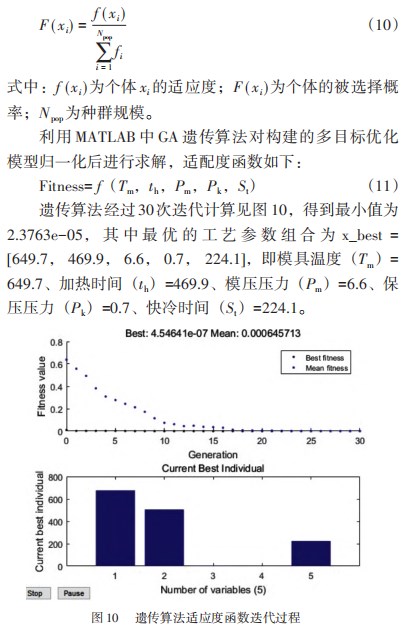
　　遗传算法是模拟生物界中遗传和进化过程的一种自适应寻优算法， 直接目标函数作为搜索信息， 不依赖梯 度信息或其他辅助知识， 只需要目标函数和适应度函数， 就可以得到较为合理的寻优结果[23-24]。

　　在遗传算法的求解过程中， 交叉概率设为 0.7. 变异 概率为 0.1. 种群规模为 100. 进化次数为 100.选择技 术采用的是轮盘赌原理 。个体选择的概率可表示为：


　　4.3 使用神经网络的遗传算法优化结果讨论与分析

　　将正交试验获得的数据作为训练样本， 为了提高神 经网络预测系统的计算可靠性， 样本数量为 32组 。基于 表 5 的样本数据， 由于在 630 ℃时， 玻璃成形能力较差， 需要足够的模压力与模压时间才能完成成形， 如表中， 成形后玻璃透镜形貌偏差达到 35.9 um (未完成形变)， 所以在进行神经网络训练时， 去掉形貌偏差很大的样本数 据 。图 11所示为神经网络训练过程的 MSE误差走势， 图 12所示为神经网络训练 、验证 、测试回归分析图， 训练 精度在 98.093%， 整体精度在百分 96.45%， 可以较为准 确地映射模压成形工艺参数同优化目标最大残余应力、成 形应力、最大形貌偏差之间的函数关系。随机挑选几组数 据检验网络系统的可靠性， 误差分析直方图如图 13所示。


　　5 结束语

　　本文提出基于有限元分析技术 、正交试验方法 、人 工神经网络及遗传算法的 BK7玻璃模压成形工艺优化方法， 对双凸透镜成形工艺进行了多元优化工艺分析 。以 模压成形工艺参数： 模具温度 、保温时间 、模压力 、加 压时间 、保压力 、慢冷时间 、快冷时间 、加热时间为决 策变量， 最大残余应力 、成形应力 、最大形貌偏差为优 化目标， 利用实验与仿真结合得到神经网络训练样本， 采用人工神经网络系统构建成形工艺参数与优化目标件 的函数关系数学模型， 并验证神经网络系统的可靠性， 接着利用遗传算法进行求最优解， 得到可靠的工艺参数， 将优化参数再反馈到仿真中， 结果表明在神经网络建模 的基础上结合遗传算法求最优解对玻璃模压成形工艺的 优化是可行的。


　　参考文献：

　　[1] Yi A Y, Jain A. Compression Molding of Aspherical Glass Lenses– A Combined Experimental and Numerical Analysis[J]. Journal of the American Ceramic Society,2005. 88(3): 579-586.
　　[2] Yi A Y, Chen Y, Klocke F, et al. A high volume precision com ⁃ pression molding process of glass diffractive optics by use of a micromachined fused silica wafer mold and low Tg optical glass [J]. Journal of Micromechanics & Microengineering, 2006. 16 (10): 2000.
　　[3] 谢晋,江宇宁,卢阔,等 . 微拱形阵列导光板快速热压成型与微 光学应用[J].光学精密工程, 2017. 25(9): 2421-2427.
　　[4] 盛斌,徐向东,刘颖,等 . 真空紫外硅闪耀光栅的制作[J]. 光学精 密工程, 2010. 18(1): 94-99.
　　[5] 周天丰,解加庆,刘洋,等 . 光学玻璃微沟槽模压成形仿真与试 验研究[J]. 光学精密工程, 2016. 24(10s): 446-453.
　　[6] Jain A. Finite Element Modeling of Structural Relaxation During Annealing of a Precision-Molded Glass Lens[J]. Journal of Manu⁃ facturing Science & Engineering,2006.128(3): 683-690.
　　[7] Sarhadi A, Hattel J H, Hansen H N.Three⁃Dimensional Modeling of Glass Lens Molding[J]. International Journal of Applied Glass Science,2015.6(2): 182-195.
　　[8] Su L, Wang F, He P, et al. An integrated solution for mold shape modification in precision glass molding to compensate refractive index change and geometric deviation[J].Optics & Lasers in Engi⁃ neering,2014. 53(2): 98-103.
　　[9] Mahajan P, Tarkes D P, Sandeep T S, et al. Optimized Design of Optical Surface of the Mold in Precision Glass Molding Using the Deviation Approach[J]. International Journal for Computational Methods in Engineering Science & Mechanics,2015. 16(1): 53- 64.
　　[10] Vu A T, Kreilkamp H, Krishnamoorthi B J, et al. A hybrid opti⁃ mization approach in non-isothermal glass molding[C]. 2016.
　　[11] Shen C, Wang L, Li Q. Optimization of injection molding pro ⁃ cess parameters using combination of artificial neural network and genetic algorithm method[J]. Journal of Materials Process⁃ ing Tech,2007.183(2-3): 412-418.
　　[12] Shi H, Gao Y, Wang X. Optimization of injection molding pro ⁃cess parameters using integrated artificial neural network model and expected improvement function method[J]. International Journal of Advanced Manufacturing Technology, 2010. 48(9- 12): 955-962.
　　[13] Hsueh-Lin W U. Optimization of Injection Molding Process Pa⁃ rameters Using the Combination of Artificial Neural Network and Genetic Algorithm[J]. Journal of North China Institute of Water Conservancy & Hydroelectric Power, 2012.
　　[14] Sun Y, Zeng W D, Han Y F, et al. Optimization of chemical composition for TC11 titanium alloy based on artificial neural network and genetic algorithm[J]. Computational Materials Sci⁃ ence,2011. 50(3): 1064-1069.
　　[15] Zhang L, Li L, Wang S, et al. Optimization of LPDC Process Pa⁃ rameters Using the Combination of Artificial Neural Network and Genetic Algorithm Method[J]. Journal of Materials Engi⁃ neering & Performance,2012. 21(4): 492-499.
　　[16] Goñi S M, Oddone S, Segura J A, et al. Prediction of foods freez⁃ ing and thawing times: Artificial neural networks and genetic al⁃ gorithm approach[J]. Journal of Food Engineering, 2008. 84(1): 164-178.
　　[17] Ghanim M S, Abulebdeh G. Real-Time Dynamic Transit Signal Priority Optimization for Coordinated Traffic Networks Using Genetic Algorithms and Artificial Neural Networks[J]. Journal of Intelligent Transportation Systems,2015.19(4): 327-338.
　　[18] Specht D F. A general regression neural network[J]. IEEE Trans Neural Netw,1991.2(6): 568-576.
　　[19] Hechtnielsen. Theory of the backpropagation neural network[J]. Neural Networks,1988(1): 445.
　　[20] Chen Y, Yi A Y, Su L, et al. Numerical Simulation and Experi⁃ ment Study of Residual Stresses in Compression Molding of Pre ⁃ cision Glass Optical Components[J]. Genetics Selection Evolu ⁃ tion Gse, 2008. 130(5): 115-133.
　　[21] Williams D, Landel R F, Ferry J D. The temperature depen⁃ dance of relaxation mechanisms in amorphous polymers and oth ⁃ er glass form liquids[J]. Journal of the American Chemical Soci⁃ ety,1995. 77(14): 3701-3707.
　　[22] Narayanaswamy O S. A Model of Structural Relaxation in Glass [J]. Journal of the American Ceramic Society,2010. 54(10): 491- 498.
　　[23] Jones G, Willett P, Glen R C, et al. Development and validation of a genetic algorithm for flexible docking.[J]. Journal of Molecu⁃ lar Biology,1997. 267(3): 727-748.
　　[24] Deb K. A fast elitist multi-objective genetic algorithm: NSGA- II[J]. IEEE Transactions on Evolutionary Computation,2000. 6 (2): 182-197.
 
 
关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/57158.html