SCI论文(www.lunwensci.com):
1 概述
边坡是人类工程活动中最为常见的一种自然地质环境,在公路、铁路、水利、市政、土建、矿山等工程中占有极其重要的地位。凡具有一定坡度的坡面均可构成边坡。边坡形成以后按其自然属性可以划分为土质边坡和岩质边坡,通常高度在30 m以下的岩质边坡与15 m以下的土质边坡可视为建筑边坡,超过这个高度,则认定为高危边坡,需进行特殊设计。特别是在地质条件复杂、人工边坡和自然边坡环境较为恶劣,降雨较多且集中的华南丘陵地区,各类工程建设遇到的边坡问题尤为突出。影响边坡稳定的因素很多,主要包括组成边坡的岩土类型及性质、边坡地质构造、边坡形态、振动作用、气候条件、风化作用坡体植被和人类工程活动等。无论多么复杂的影响因素,最终形成滑坡事故都可归结为滑动体沿滑动面滑动形成坡体失稳。按失稳后可能造成的破坏后果(危及人的生命、造成经济损失、产生社会不良影响)的严重性、边坡类型和坡高等因素,可将边坡工程安全等级划分为三级。事实上,一个边坡工程的各段,可根据实际情况采用不同的安全等级,而对于危害性严重、环境和地质条件复杂的特殊边坡工程,其安全等级可根据实际情况适当提高。边坡安全等级分类方法相对灵活、直观,是根据边坡可能产生的危害大小定性分类的方法,对于具体管道与边坡相互关系,以及边坡内部各种力学性能,并未给出量化关系,在实际工程治理中,其反映的定性关系对管道边坡评价与指导意义不大[1-3]。
我公司高压燃气管道有约98 km地处山区,近年来深圳市在龙华、坪山等高压、次高压管道密集地区兴建了众多公用设施,形成共约398个边坡,给管道管理工作带来重大挑战。为深刻吸取“光明12·20重大滑坡事件”的教训,对为数众多的燃气管道边坡开展治理迫在眉睫,但是目前就管道边坡治理顺序问题没有既有方案供参考。本文根据边坡具体参数展开理论计算,计算出边坡滑动体被扰动瞬间形成的最大剪力标准值,定义边坡管道安全度为该最大剪力与管道能承受的最大剪力标准值的比值P,通过边坡管道安全度判断边坡管道是否安全,从而为政府部门和相关企事业单位对边坡管道开展有序的治理工作提供参考。
2 边坡管道安全度计算流程
为有效评价边坡管道安全问题,提出边坡管道安全度理论。该理论以敷设燃气管道的边坡为研究对象,以边坡失稳瞬间形成的最大剪力标准值为切入点,通过比较最大剪力标准值与管道能承受的最大剪力标准值来定量分析边坡管道安全性,形成边坡管道安全度分析流程,见图1。
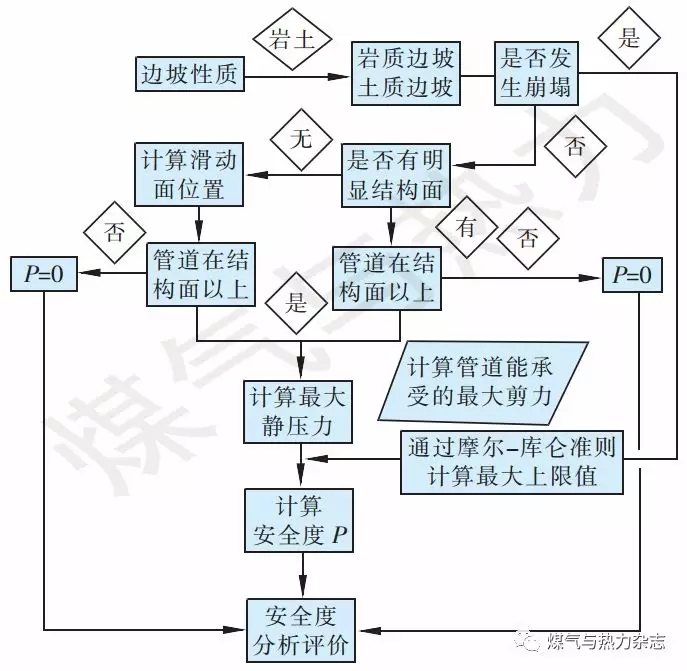
图1 边坡管道安全度分析流程
滑坡发生时,滑动体与不动体之间形成的界面称为滑动面,坡体发生滑动通常以软弱结构面为滑动面[4-5],所谓软弱结构面是指力学强度明显低于围岩,具备一定厚度的泥化、软化或破碎的岩层。如果管道所在边坡存在明显软弱结构面,可根据现场情况,确定上敷岩土层土方量最大的软弱结构面为滑动面,以此计算出的极限剪力为坡体受扰动可能形成的最大剪力,来确保管道安全度计算值更可靠[6]。如果坡体没有明显软弱结构面,则通过极限平衡法展开理论计算,确定滑动面位置,位置确定以后结合管道与结构面位置计算最大上限土压力标准值;如果边坡为表面发生崩塌,则结合摩尔-库仑准则计算坡体自上而下发生崩塌破坏时可能出现的上限剪力标准值,通过岩土破坏时的剪力与管道能承受的最大剪力之间的关系计算边坡管道安全度。
摩尔-库仑准则是岩土体发生破坏时的应力组合关系,是岩土力学领域被广泛接受和运用的基本理论[7-8]。根据该理论,边坡的强度参数主要由2个参数决定:粘聚力c和内摩擦角φ。任意一点在某一平面上的剪应力达到岩土体的抗剪强度,即可使岩土体屈服。岩土体发生破坏时的极限应力计算公式见式(1)。
坡体发生扰动从本质上可认为是坡体自身原有的平衡被打破,坡体受力增加或结构面粘结性能减弱。根据摩尔-库仑准则我们知道,摩尔包容线位于抗剪强度圆外边,可知边坡发生扰动时的实际破坏力小于极限平衡的上限力,而极限平衡的上限力可以通过理论计算来进行评估,通过扰动上限力与管道抗剪性能的关系可以定量评价管道安全程度。坡体扰动上限力可视为滑动面以上整个坡体施于管道的最大力,因此需要依据文献[8]提出的研究方法,根据既有边坡展开结构面位置的研究,根据结构面与燃气管道的空间位置关系来计算加载于管道上的最大剪力。
3 管道边坡安全度研究
管道通常沿平行或斜交于边坡走向的方向敷设,沿坡体表面起伏敷设的情况相对少见,下面就管道沿坡体走向的方式展开受力研究,计算边坡管道安全度。
3.1 坡体敷设管道极限受力情况
管道边坡通常是在管道敷设以后,由于受到某种扰动使原有的应力平衡打破,进而发生坡体滑动等破坏,就山地高压燃气管道而言,这种外在应力一般与重力的迅速增加、结构面强度迅速减弱有关[7]。边坡形成后,受外在扰动的机会和应力一般较小,通常是由于自身重力增加来打破受力平衡,而降雨是造成坡体重量增加的主要形式。在有明显软弱面存在的边坡体,坡体沿覆土层最厚的软弱面滑动时对管道冲击最大,管道本体受到的极限剪力为主动土合力值,计算方法依据GB 50330—2013《建筑边坡工程技术规范》,见式(2)和(3)。如果边坡岩质土质均匀,无明显软弱面存在,且管道坡体岩质与土质相对均匀,则可以反推结构面,结构面位置确定后再根据式(2)和(3)计算;如果坡体表面已经发生崩塌,则按照摩尔-库仑准则极限受力展开计算,见式(4),计算出剪力后再根据管道长度,计算土压力标准值,见式(5)。
3.2 边坡管道安全度计算
安全度是安全系统工程学的一个概念,是将事故风险值量化的一个指标。对于边坡管道而言,其安全度是评价边坡发生事故时,管道受到潜在影响(风险)的一个量化值,是定量研究边坡管道安全问题的参数。
定义边坡管道安全度是滑坡发生瞬间管道受到的最大剪力与管道能承受的最大剪力标准值的比值,见式(6)。
式(6)中的σpipe根据空心圆截面惯性矩、受内压作用的圆柱壳轴向应力公式和简支梁屈服理论,设定材料屈服强度为屈服上限,由计算机编程计算[9]。
当P>1时,一旦滑坡事故发生,则造成的损失相当巨大。这类边坡在勘探过程中要反复论证,取多处测试点进行验证,同时运用FLAC3D等相关专业软件,多次模拟确认。通常这类边坡属于高危复杂边坡,在管道的路由选择上要尽量避开,如果无法避开,则在设计、施工初期,优先考虑对这类边坡进行治理。
当P=1时,视为滑坡发生的临界状态,此时如果边坡外在扰动消失,则滑坡可以制止,管道充当了加固边坡的锚锁。
当P<1时,发生滑坡时坡体对管道造成的扰动相对管道强度来说可以承受,不会从根本上对管道造成破坏。
4 边坡安全分析实例
目前深圳市城市燃气输配系统高压管道路由经过山地边坡较多,近年来受道路交通、电力电缆、轨道交通等市政建设影响形成的人工边坡相对较多,相关单位已经展开治理,运用边坡管道安全度理论展开研究,给大数量、多类型管道边坡分期治理提供依据。
4.1 坂澜大道双阀室东边坡
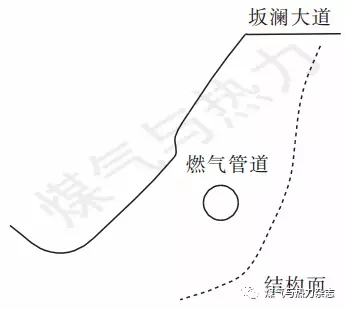
坂澜大道双阀室东边坡,现状松散土质主要来自坂澜大道施工,是典型人工边坡。边坡结构面明显,水土流失严重。现场探测显示,管道位于基岩以上,表土层内,基岩岩质较硬,节理发育不明显,基岩与松散土层交界部位构成明显结构面,根据现场测量,绘制该边坡断面图,见图2。
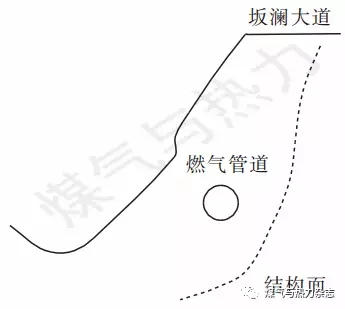
图2 边坡断面图
管道位于结构面以上,采用式(2)、(3)计算最大土压力。其中,k取上限最大可能值2,γ取19.6 ×103 N/m3,Ka取1;边坡高度h测量为15 m,计算得出σ=4.41×106 N/m。管道公称直径500 mm,为L360钢管,运行压力1.5 MPa,管段在坡体处的长度为14 m,使用计算机编程计算得出管道所能承受的土压力标准值σpipe=5.9×103 N/m。根据式(6),P>1。计算结果表明该边坡管道安全度大于1,属于高危边坡管道。
4.2 坂澜大道Z145号桩边坡
坂澜大道Z145号桩边坡为岩质边坡,上部覆盖表土层厚度为2~3 m,边坡已经出现崩塌现象,水土流失现象相对严重,受道路建设影响,形成的坡度较大,边坡平均倾斜角在75°以上。但是,该边坡岩质较好,节理发育不明显,整体连续性强,相对稳定。
现场调查测量发现,管道于边坡表土层敷设,埋设深度约2 m左右,滑坡部位位于Z145桩部位附近,滑坡呈漏斗形,上宽下窄,崩塌顶部宽约3 m左右。覆盖层沉积较好,除崩塌部位无明显软弱面存在,可认为是均匀土体,土体覆盖厚度为2~3 m。
该边坡的特征图见图3,土壤胶结性好,上部无明显外力施加,且排水良好,在单纯降雨条件下重力增加不明显,无明显结构面,不足以使边坡整体造成损害。根据摩尔-库仑准则,假设边坡发生滑动,采用式(4)、(5)计算最大土压力。崩塌部位以下岩土体致密,管道覆土层为粉砂土均匀沉积,取ρ=2.0×103 kg/m3。岩土体根据GB 50330—2013认定为IV类边坡,结合结构面崩塌情况,外倾结构面倾角认定为35°,土壤粘结力c取8 kPa[10],内摩擦角参照结构面倾角取35°,崩塌部位长度3 m。计算得出σ=106.32×103 N/m。使用计算机编程计算得出管道所能承受的土压力标准值σpipe= 130×103 N/m。
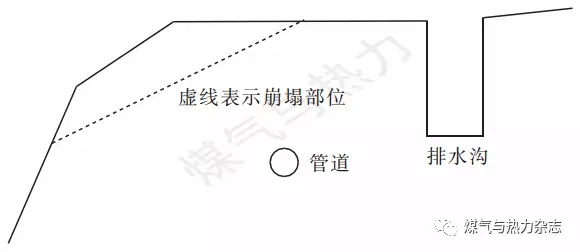
图3 坡体崩塌部位断面图
根据式(6),P<1,崩塌对管道产生的土压力小于管道最大承压能力,因此该边坡可定性为管道处于结构面以下的情况,表土层冲刷对管道本体无明显影响,即使不治理该边坡,对管道本体造成伤害的可能性也不大。
5 结论
①基于岩土力学极限平衡法,反推边坡结构面计算公式,比较边坡结构面与管道空间关系,确定不同类型边坡,用不同的方法计算边坡,可能施加给管道的最大剪力。
②定义边坡管道安全度P并给出计算公式,分析P值在不同范围内管道与边坡的安全关系。P<1是相对安全边坡,对管道安全影响较小,反之,则需尽快治理边坡。
参考文献:
[1]杨学堂,王飞. 边坡稳定性评价方法及发展趋势[J]. 岩土工程技术,2004,18(2):103-106.
[2]孙玉科,杨志法,丁恩保. 中国露天矿边坡稳定性研究[M]. 北京:中国科学出版社,1999:97-112.
[3]郑颖人,时卫民,杨明成. 不平衡推力法与Sarma法的讨论[J]. 岩石力学与工程学报,2004,23(17):3030-3036.
[4]陈祖煌. 土坡稳定分析通用条分法及其改进[J]. 岩土工程学报,1983,5(4):11-26.
[5]汪承亮. 极限分析法在边坡稳定分析及挡土墙土压力计算中的应用(硕士学位论文)[D]. 合肥:合肥工业大学,2010:20-35.
[6]刘立平,姜得义,郑硕才,等. 边坡稳定性的最新进展[J]. 重庆大学学报(自然科学版),2000,23(3):115-118.
[7]赵明阶,何光春,王多垠. 边坡工程处治技术[M]. 北京:人民交通出版社,2003:1-6.
[8]孙志彬. 边坡稳定性上限分析法及参数反演研究(博士学位论文)[D]. 长沙:中南大学,2013:30-45.
[9]帅健,于桂杰. 管道及储罐强度设计[M]. 北京:石油工业出版社,2006:9-162.
[10]孙晓东,王丹. 土的粘聚力取值分析 [J]. 辽宁建材,2010(3):39-41.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/141.html