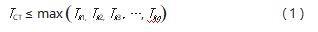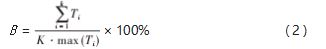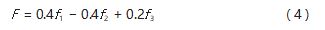SCI论文(www.lunwensci.com)
摘要:为实现装配线生产工序的平衡优化, 采用改进遗传算法, 以装配线生产节拍、平衡率和平滑指数为优化目标, 建立装配线 平衡优化模型。采用基于紧前工序约束的交换变异方法, 并与父代进行优劣对比, 有效避免无效基因的产生。引入精英保留策略, 提高算法寻优能力及收敛速度。以波轮洗衣机机芯装配线的平衡优化为例, 验证前述算法的可行性。结果表明: 与原方案相比, 优化后的生产节拍为 17.2 s, 减少了 0.8 s; 生产平衡率达到 90 %, 提高了 18 %; 平滑指数从 1.3 减少到 0.72. 验证了所提出的模型 算法可以有效优化该装配线的生产节拍、平衡率、平滑指数, 从而优化其生产效率。
Research on Assembly Line Balance Optimization Based on Improved Genetic Algorithm
Long Jialing1. Zhang Cunji1. Ning Lihua2. Gao Xingyu1
( 1. Guangxi Key Laborotory of Manufacturing Systems and Advanced Manufacture Technology, Guilin University of Electronic Technology,Guilin, Guangxi 541004. China;
2. School of Methematics and Computing Science, Guilin University of Electronic Technology, Guilin, Guangxi 541004. China) Abstract: In order to realize the balance optimization of assembly line, improved genetic algorithm is adopted, and the production beat, balance rate and smoothness index of assembly line are taken as the optimization objectives to establishe an assembly line balance optimization model. The exchange mutation method based on the constraint of immediate preceding process is adopted to effectively avoid the generation of invalid genes. The elitist preservation strategy is introduced to improve the optimization ability and convergence speed of the algorithm . The balance optimization of pulsator washing machine movement assembly line is taken as an example to verify the effectiveness of the above algorithm. The results shows that compared with the original scheme, the optimized production beat is 17.2 s, reducing 0.8 s; the production balance rate is 90%, increasing 18%; and the smoothing index is reduced from 1.3 to 0.72. which proves that the production beat, balance rate and smoothing index of the assembly line can be effectively optimized by using the proposed model algorithm, so as its production efficiency can be optimized.
Key words: improved genetic algorithm; assembly line balancing; elitist preservation
0 引言
近年来, 随着智能制造技术的不断发展, 中小型制 造企业在数字化转型的竞争中, 生产智能化水平面临着 极大挑战。整机产品的装配线是制造型企业的核心生产 环节, 一般是多个工作站由传送带或移动带相互连接, 通过在给定的时间内重复执行一组特定的操作来组装单 个产品[1]。为最大化生产效率, 中小型制造企业需要对 车间人员配置、物流运输、生产流程、制品管理等方面 进行及时优化, 以适应当前多品种小批量的产品特性。 尤其是核心的装配环节, 在可装配多种型号产品的混装 装配线的广泛应用下, 装配线平衡方法的实现至关重要。 装配线平衡是指将某型号产品的各装配工序, 在满足紧前紧后工序的约束下, 将单个工序分配到不同的工作 站[2], 以达到人、机、料、法、环的最优生产配置的目的。
装配线平衡问题属于 NP-hard 组合优化难题[3], 需在 有限个可能解的集合中找到离散事件的最优解。王公 臻[4]将装配线平衡问题进行了分类及建模, 即 SALBP- Ⅰ 和 SALBP- Ⅱ两大类问题。第 Ⅰ 类问题为在生产节拍不 变的情况下, 以工位数最小化为优化目标, 达到降低生 产成本的目的。第Ⅱ类问题为在规定的工位数不变的情 况下, 以生产节拍最小化为优化目标, 以达到缩短工时、 提高生产效率的目的。
当前, 国内外对装配线平衡优化已经进行了大量研 究。陈帅等[5] 提出了多目标蚁狮算法, 引入基于牛顿二分法的解码装配任务方法来解决第二类多目标装配线平 衡问题。管梦竹等[6] 提出了混合果蝇算法, 该方法能够 有效求解第一类多约束双边装配线平衡问题。
遗传算法作为通过借鉴生物进化论而构造的并行随 机搜索最优化方法, 在解决装配线平衡问题上有独特的 优势。 LEU 等[7] 开创使用遗传算法求解简单装配线平衡 问题的先河, 证实了利用遗传算法的解决方案显著优于 传统的启发式解决方案。 M Dalle Mura 等[8]采用遗传算法 对流水线型企业装配线平衡进行了多目标优化。杨磊 等 [ 9 ] 设计了双种群遗传算法, 并建立了混流生产线第二 类平衡问题的多目标混合整数规划模型, 有效地解决和 改善了第二类混流生产线平衡问题。韩煜东等 [ 10 ] 设计 出基于自然数序列编码策略和拓扑排序理的改进遗传算 法并提出种群扩张机制, 有效解决了混合装配线多目标 优化问题。李明等[11]设计了基于任务排序的种群初始化 方法的改进遗传算法, 进行了多目标装配线平衡优化。
基于以上分析, 装配线再平衡问题是典型的多目标 优化问题[12], 本文以最小化生产节拍、最大化产线平衡 率和最小化平滑指数为优化目标, 建立装配线再平衡优 化模型, 设计改进的遗传算法对平衡模型进行求解, 按 照作业优先顺序对其工序进行重新编排, 从而得到一组 最优的工序作业方案。以波轮洗衣机机芯装配线作为实 际案例验证算法的可行性, 结果表明: 优化后的装配线 减少了生产节拍, 提高了生产线平衡率和降低了生产线 均衡指数, 从而提高了企业整体生产效率和效益。
1 目标装配线平衡问题描述
装配线平衡问题即在根据生产需求计算装配线理论 生产节拍的情况下, 对其最优工位数进行求解, 再对其 可能解进行适应度对比, 选出理论最优解。各工位负责 的工序分配完毕后, 即确定了最优工位数 K后, 以达到 最小生产节拍 TCT, 最大平衡率 B 和最小平滑性指数 S 的 优化目标。
本文的装配线平衡优化问题中, 不考虑机器故障、 工人请假、订单取消, 忽略工人行走所花费的时间, 并 忽略工序加工之间的转移时间, 优化目标表述如下。
( 1) 优化目标1: 生产节拍TCT 最小, 如式 (1) 所示。
式中: TCT 为生产节拍; k 为工位索引, k=1. 2. 3. …, n; Tk 为 k号工位的作业时间。
( 2) 优化目标 2: 平衡率 B最大, 如式 (2) 所示。
式中: B 为平衡率; K为工位数; Ti 为第 i号工位的作业 时间。( 3) 优化目标 3: 平滑性指数 S最小。
式中: S 为平滑指数; a 为工序索引, a=1. 2. 3. …, m; Ta 为第 a个作业的作业时间。
2 设计改进的遗传算法
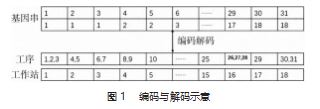
将遗传算法运用于装配线平衡优化已经非常普遍, 且简单快捷, 遗传算法具有良好的稳定性和全局寻优能 力。本文设计了一种改进的遗传算法用于解决机芯装配 线平衡问题, 满足所提出的优化目标, 遗传算子的设计 与选择会直接影响到所产生的可行解的可靠性与多样性, 因此本文提出一种考虑紧前工序的交换变异方法, 并且 与父代进行优劣对比, 避免无效基因的产生; 引入了精 英保留策略, 保护后期优秀个体, 提高了算法寻优能力。 2.1 编码与解码假设需要将 n个工序分配给 m个工作站, 则需要将 作业工序编号与工作站编号对应。采取自然数编码后, 得到长度与工序数相同、编码为 n 的数据串, 基因序号 即为工序编号, 基因值标识即为负责该工序的工作站编 号。编码与解码如图 1 所示。
2.2 适应度函数
本文所建立的优化模型如前文所述, 适应度本质即 为优化问题的目标函数。考虑到收敛方向一致, 将平衡 率目标函数取负; 考虑平滑性指数受生产节拍与工位数 影响, 而生产节拍与平衡率的评价相对独立, 将生产节 拍与平衡率权重定为 0.4. 平滑性指数定为 0.2.本文提 出如式 (4) 所示的适应度函数。
式中:f1 为目标函数 1;f2 为目标函数 2;f3 为目标函数 3.
2.3 选择
本文采用经典的轮盘赌选择方法, 在该方法中, 每 个个体的选择概率和其适应度值成正比例, 根据其“累 积概率”进行选择, 设种群大小为 t, 个体p 的适应度为F (p), 则 S (p) 为个体p 的累积概率, 其公式如下:
2.4 交叉
本文采用 PBX 交叉算子, 操作如下: 随机选择父代1、父代 2. 随机选择父代 1 中的几个基因位置, 位置可 以不连续, 再将选中的基因按照位置复制到子代中, 最 后删除父代 2 中父代 1 选中的基因位置, 剩下的部分按照 顺序填入子代。交叉操作如图 2 所示。
2.5 变异
随机挑选一个父代变异染色体, 然后随机产生 1 个 变异点, 找到这个点的紧前工序点, 紧前工序点前的 排列不变, 该变异点与紧前工序后的随机位置进行交 换。完成 1 次变异后, 该变异基因与父代基因进行适 应度对比, 优则保留, 劣则放弃此次变异。变异操作 如图 3 所示。
2.6 精英保留
对于遗传算法来说, 能否做到收敛到全局最优解是 最首要的功能, 为了防止当前群体的最优个体在下一代 丢失, 导致遗传算法不能收敛到全局最优解, 本文采用 精英保留 (Elitist Preservation, EP) 策略[13] 用于保护当 前群体的最优个体。该策略的思想是不将群体在进化过 程中迄今出现的最好个体 (称为精英个体 elitist) 进行配 对交叉而直接将它复制到下一代中。这种选择操作又称 为复制 (copy)。精英保留策略可以避免最优个体因杂交 操作而被破坏。
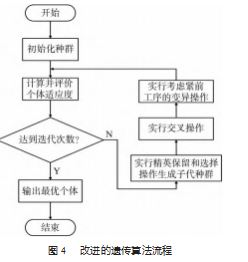
2.7 算法流程
本改进遗传算法流程如图 4 所示。随机初始化种群 后, 对 18 个工位以及 31 道工序进行自然数编码, 将每个 工位负责的工序及其所需时间储存在染色体中, 再进行 算子操作与迭代优化。具体步骤如下:
( 1 ) 设置参数后, 随机生成一组初始种群;
( 2 ) 计算并评价个体适应度;
( 3) 先采取精英保留策略, 保留一定概率的优秀染 色体, 再使用轮盘赌选择算子进行选择操作;
( 4) 根据概率挑选个体, 采用 PBX 交叉算子进行交 叉操作;
( 5) 根据概率挑选个体, 采用考虑紧前工序的交换 变异算子进行交换操作, 并与父代进行适应度对比后, 择优选取;
( 6) 继续执行步骤 2. 直到迭代次数达到程序预定, 最后输出种群中的最优个体。
3 实例验证
3.1 波轮洗衣机机芯装配线数据
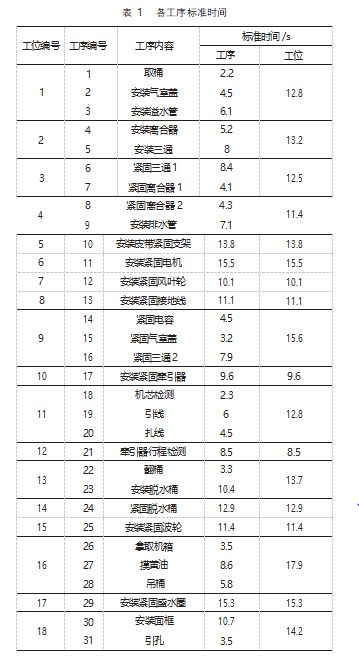
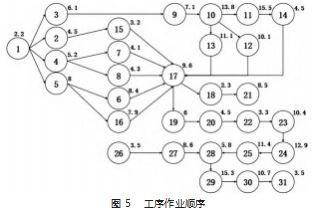
本文采用宁波正电电器波轮洗衣机机芯装配线的数 据, 该装配线由 18 个工位和 31 道工序组成, 运用秒表法 测量机芯装配线各工序的工时, 得到各工序标准时间如 表 1 所示。由表可得机芯装配线的工序作业顺序如图 5 所 示。图中带数字的圆圈表示机芯所经过的 31 道工序, 圆 圈旁的数字表示工序标准作业时长, 箭头则表示作业的 先后约束关系。
根据历史销售数据和销售预测, 目前实际每天需要 生产数量为 1 600 件, 装配线的每日工作时长为 8 h。由此计算出理论生产节拍:
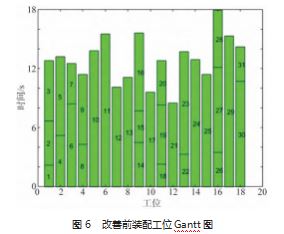
根据式 (6) 可知, 改善前的理论生产节拍为 18 s, 再通过计算式 (2) ~ ( 3) 可知, 改善前的线平衡率 为 72%, 平 滑 指 数 为 1.32 。 原 始 工 位 甘 特 图 如 图 6 所 示 。
3.2 参数设置及优化
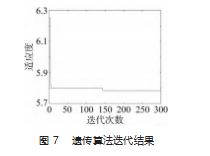
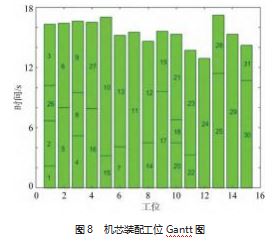
基于上述算法思路与数据, 本文采用仿真工具 MAT⁃ LAB 进行算法实现及平衡方案求解, 参数设置为生产节 拍 TTT=18 s, 种群大小 s=80. 进化代数 G=300. 交叉概率 Pc=0.9. 变异概率 Pm=0. 1. 精英保留比例 Pe=0. 1.迭代结 果和工位甘特图分别如图 7~8 所示。
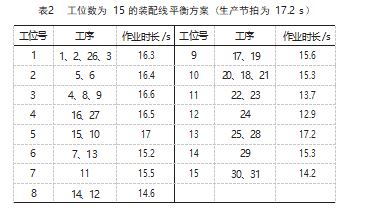
由图可知, 优化后 机芯装配线工位数为 15 时, 得到最优方案。工位数为 15 时的机芯装配线平衡方案如表 2 所示。根据式 (1) ~ ( 3) 计算出该方案的生产节拍、生产线平衡率和均衡指数, 可得生产节拍 TCT 为 17.2 s、装配线平衡率 B为 90%、 最小平滑性指数 S 为 0.72.说明该改进遗传算法显著降 低了生产线的生产节拍与平滑性指数, 提高了生产线平衡率, 可有效解决机芯装配线平衡问题, 对离散装配企 业生产有积极意义。生产需求; 机芯装配线总平衡率提高了 18%; 同时工位 数量和平滑指数均为最小。由此可知改善后机芯装配线 效率较高, 负载更均衡, 运行更顺畅, 装配线平衡优化 的同时也提高了整体生产效率。装配线平衡改善前后对 比如表 3 所示。
4 结束语
本文构建了装配线平衡优化数学模型, 通过求解最 小化生产节拍, 最大化产线平衡率以及最小化平滑指数, 以达到提高机芯装配线效率,使负载更加均衡且运行更加 顺畅的优化目标。此外, 在本文所提出的改进遗传算法 中,考虑紧前工序的交换变异方法,并与父代进行适应度 对比,可有效避免无效基因的产生,减少计算量;引入精 英保留策略, 提高了算法寻优能力及收敛速度。最后, 以波轮洗衣机机芯装配线为实例, 验证了算法的可行性。
通过 MATLAB 完成算法的实现与最优方案的输出, 与原始方案相比, 改进后的新方案的生产节拍从 18 s 减 少到 17.2 s; 生产线平衡率达到了 90%, 提高了 18%。结 果表明: 所提改进遗传算法能够有效优化该装配线的生 产节拍、平衡率、平滑指数, 从而优化其生产效率。在 后续的研究中, 可以进一步提高精确度, 并且可以将本 文算法应用于其他装配线的平衡问题。
参考文献:
[1] SCHOLL A, KLEIN R. Balancing assembly lines effectively: A computational comparison[J]. European Journal of Operational Research,1999.114(1):50-58.
[2] 李梓响,唐秋华,毛永年,等 . 迭代局部搜索求解双边混流装配线平衡问题[J]. 机械设计与制造,2016(3):54-57.
[3] GUTJAHR A L,NEMHAUSER G L. An algorithm for the line bal⁃ ancing problem[J].Management Science,1964.11(2):308-315.
[4] 王公臻 . 大规模生产线平衡问题的模型及求解研究[D ]. 北京: 北京交通大学 .
[5] 陈帅,晁永生,江韩 . 蚁狮算法在第二类多目标装配线平衡问题 中的应用[J]. 组合机床与自动化加工技术,2021 (12):136- 139.
[6] 管梦竹,原丕业, 王淑玉 . 基于混合果蝇算法的双边装配线平 衡问题研究[J/OL]. 计算机集成制造系统:1- 16[2022- 10-31]. http://kns. cnki. net/kcms/detail/11.5946. tp. 20221017.1706.002. html.
[7] LEU Y Y,MATHESON L A,REES L P. Assembly line balancing using genetic algorithms with heuristic-generated initial popula⁃ tions and multiple evaluation criteria[J]. Decision Sciences,2010. 25(4):581-605.
[8] DALLE MURA M, DINI G. A multi-objective software tool for manual assembly line balancing using a genetic algorithm[J].CIRP Journal of Manufacturing Science and Technology,2017 (6): 72-83.
[9] 杨磊,徐晓鸣,张海洋,等 . 基于双种群遗传算法对 A 公司生产线 改造以及平衡问题研究[J]. 机电工程技术,2022.51(5):170- 173.
[10] 韩煜东,董双飞,谭柏川 . 基于改进遗传算法的混装线多目标 优化[J]. 计算机集成制造系统,2015.21(6):1476- 1485.
[11] 李明, 包建军,袁逸萍 . 基于改进遗传算法的多目标装配线平 衡优化研究[J]. 机械设计与制造,2022(4):204-207.
[12] TSAI L H. Mixed-model sequencing to minimize utility work and the risk of conveyor stoppage[J]. Management Science. 1995 (41):485-495.
[13] 杜晓亮, 张楠,孟凡云,等 . 改进 NSGA2 算法求解柔性作业车间 调度问题[J]. 组合机床与自动化加工技术,2022(5):182- 186.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/65273.html