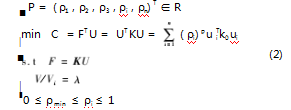SCI论文(www.lunwensci.com)
摘要: 为减轻焊条自动计量机构重量, 提高结构的整体性能, 采用有限元分析和结构拓扑优化方法对计量盘进行轻量化设计。确定 了计量盘模型的材料和初始参数, 分析出计量盘模型在正常运转时 4 个工况的受力模型, 通过有限元静力学分析校核了计量盘在所有工况下的刚度。基于变密度法以结构柔度为目标函数, 以应变能为优化约束条件建立了计量盘拓扑优化数学模型。将优化的模型简化处理后利用 Lanczos 迭代法表征振动特征值和激励响应进行模态分析。优化结果表明: 计量盘的重量比原结构降低了 48.4% ,低阶固有频率降低, 相同静载荷条件下, 最大等效应力最大位移均有所增加, 优化后模型仍满足结构刚度要求。焊条计量盘模型远 离外部激励频率, 轻量化效果较为明显。
关键词: 焊条自动计量机构,静力学分析,拓扑优化,模态分析,轻量化
Topology Optimization Design of Measuring Panel of Electrode Automatic Measuring Mechanism
Xu Xiangqian, Yang Peijing
(School of Materials Science and Engineering,Xi'an Petroleum University,Xi'an 710065.China )
Abstract:In order to reduce the weight of the automatic welding rod metering mechanism and improve the overall performance of the structure,finite element analysis and structural topology optimization methods were used to design the lightweight metering disk.The material and initial parameters of the metering disk model were determined,and the force models of the metering disk model under 4 working conditions were analyzed during normal operation.The stiffness of the metering disk under all working conditions was checked through finite element statics analysis.Based on the variable density method,taking the structural flexibility as the objective function and the strain energy as the optimization constraint condition,the mathematical model of the metering disk topology optimization was established.After simplifying the optimized model, the Lanczos iteration method was used to characterize the vibration eigenvalue and excitation response for modal analysis.The optimization results show that the weight of the metering disk is 48.4% lower than the original structure,the low order natural frequency is reduced,the maximum equivalent stress and maximum displacement are increased under the same static load conditions,and the optimized model still meets the structural stiffness requirements.The electrode metering disk model is far away from the external excitation frequency,and the lightweight effect is obvious.
Key words:automatic electrode measuring mechanism;static analysis;topology optimization;modal analysis;lightweight
0 引言
针对于国内焊条存储计量机构的研究短缺, 焊条自 动计量机构同时具备焊条存储 、分类和计数功能, 便于 实际加工生产中工人准确拿取和仓库管理人员记录焊条 情况。为了减轻焊条计量盘的重量, 提高焊条自动计量 机构整体性能, 对焊条计量盘进行结构优化设计。 目前 结构优化主要有形状优化 、尺寸优化 、拓扑优化 3 个类 型 [1], 在这 3 种优化设计中, 拓扑优化对于结构的设计 变量更多 、材料优化效果更加明显 、具有更大的设计空 间和发展前景, 拓扑优化的思想是考虑目标函数约束下 计算优化设计区域的材料分布最优解[2] 。对于二维壳体 和三维实体等连续体拓扑优化主要有均匀化方法 、基结构方法 、变密度方法 、水平集算法 、渐变优化算法等[3] 。 焦洪宇 、周奇才等[4] 基于变密度法的体积约束下, 以结 构最小柔度为目标函数进行周期形拓扑优化达到了桥式 起重机的轻量化; 李英磊等[5] 基于变密度法建立飞机隔框结构数学模型, 在最优化准则方法下引入拉格朗 日公式计算拓扑优化结果, 总体减重了 38.2% 。
本文以某焊条自动计量机构计量盘为研究对象, 从 材料和结构等优化方面对计量盘进行了轻量化设计。确 定尼龙为初始材料, 以计量盘整体柔顺度为 目标函数、 减少 30% 的体积为约束条件, 基于变密度法对计量盘进 行了拓扑优化设计。最后对优化后的模型进行了静力学 和模态分析, 进一步印证了优化方案的可行性。
1 数学模型建立
变密度法[6] 是以每个单元的伪密度作为常数并引入 0 ~ 1 的伪密度取值范围[7], 建立伪密度和材料特性之间的显示函数关系, 其理论公式如下:
式中: E 为弹性模量; η为单元密度; E0 为实际材料属 性; ν为泊松比。
在实际迭代运算过程中, 每个单元的材料物理属性 伴随单元的密度改变发生变化, 保留单元和去除单元为 小于或大于接近 1 或 0 的某一特定值。但针对于模型单 元中伪密度在 [0. 1] 中间范围的数值, 需要引入插值 来惩罚模型解决原变密度法中仅出现 0 或 1 的离散现象。 文中使用 SIMP 插值方法优化数学模型, 优化网格依赖 问题[8] 使中间函数值向两边靠拢从文献 [9] 得知 p 取 值为 3 时可方便计算算法收敛。
以密度为设计变量, 体积为约束条件, 结构的总柔 度 (刚度) 为目标函数, 基于 SIMP 插值的变密度建立 拓扑优化数学模型, 其公式如下:
式中: ρ为每个单元密度矢量; C 为整体机构柔度; F 和 U 分别为结构的外部载荷和位移; K 为整体结构刚度矩 阵; Vi 和 V分别为单元初始体积和优化目标体积; ρmin 为 单元密度值下限, ρmin 一般取值为接近于 0 。
2 有限元模型建立与分析
2.1 初始模型建立
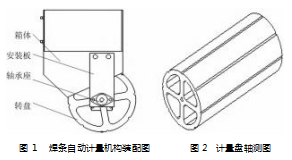
利用 Solidworks 软件建立焊条自动计量机构三维模型, 图 1 为焊条自动计量机构。计量盘通过轴承座和安 装板螺栓连接与箱体固定, 其工作流程为: 操作管理人 员将焊条放进箱体内, 机构整体通过控制电机制动带动轴和计量盘转动达到焊条存取和计数目的。为了减轻机 构整体重量和电机负载, 需要计量盘在达到轻量化的同 时满足强度和刚度要求 。 图 2 为计量盘轴测图, 具体参 数: 长 380 mm, 外径 180 mm, 内径 150 mm, 圆槽大小 8 mm ×小6 mm 。
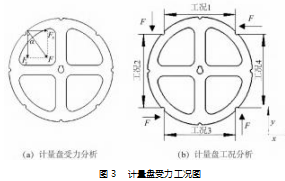
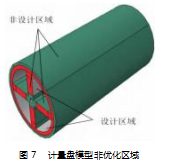
焊条自动计量机构正常运转时, 计量盘主要承受箱 体内焊条的压力。如图 3 ( a ) 所示, 红色部分为初始放 入焊条时计量盘受力区域, 焊条实际施加的压力为 Fy 。 结合计量盘中间翼梁为实际主要承载情况, 近似将其受 力分成工况 1 、工况 2 、工况 3 和工况 4. 如图 3 (b) 所 示。以工况 1 为例, 当计量盘受力区域变成工况 1 所示时, 通过施加 F 力等效 Fy 力的影响 。 箱体内初始可存放7.8 kg 的焊条, 即 Fy =76 N, 与 F 力夹角 α=45°, 经三角函数计算 F 值大小为 108 N 。计量盘承受压力随着机构 运转时焊条减少而降低, 为方便受力分析同时满足实际 载荷施加要求对计量盘受力区域简化成全部施加 F 大小 的均布压力, 各工况的受力方向和区域为图3b 箭头所指 方向, 大小为 108 N 。
2.2 材料属性设定
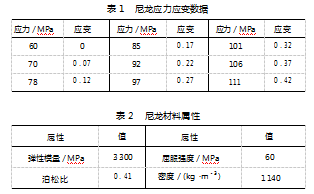
为了最大程度减轻计量盘重量, 计量盘选用尼龙材 料。塑性材料在进行静力学分析前需要输入其应力应变 数据建立数据库, 在塑性变形阶段尼龙应力和应变数 据 [10] 如表 1 所示, 其物理材料参数如表 2 所示。
2.3 模型建立与分析
将计量盘模型导入 Abaqus 软件 Part 模块实体单元, 选用 Abaqus 自带的 Mesh 模块进行计量盘模型网格划分。 模型网格划分采用整体划分, 网格类型均为六面体网格 单元 。为了提高网格质量和结果分析精准度, 将模型 分割成比较简单的区域, 同时对模型进行简化: 忽略 计量盘圆槽 、圆角等对分析结果影响不大的部分 。计 量盘模型网格类型为 C3D8R, 单元总数 31 311 个, 网 格节点数 40 448 个, 图 4 为简化处理后网格划分的有 限元模型 。
定义模型边界条件和受载情况, 以工况 1 为例, 针对其受力方向和受力区域, 通过 Abaqus 的 Interaction 模块耦合功能对计量盘耦合区域在-Y 方向施加 108 N 大小的载荷。根据机构中计量盘运动方式对其添加转动约束, 同样采取耦合方式, 并在 Load 模块的位移/转角条件约 束耦合点 X、Y、Z 方向全部自由度。如图 5 所示, 图中 绿色区域为受力区域, 箭头 A 所指红色区域范围为边界 条件施加区域。由材料力学强度理论可知, 当结构中材料应力值达 到超过屈服强度或抗拉强度临界值时, 材料就会产生永久变形或者断裂现象, 因此计量盘模型中的最大应力值 应小于材料的许用应力 [ σ] 。从图 6 的 4 种工况云图可以看出最大应力都位于计量盘中心转轴处, 4 种工况最大等效应力为 0.023 MPa, 基于 Von mises 屈服准则进行尼龙材料[11] 的计量盘结构分析, 其公式为:
( σ1 -σ2 ) 2 -( σ2 -σ3 ) 2 -( σ3 -σ1 ) 2 σ(3) 式中: σr 为等效应力; σ1 、σ2 、σ3 分 别为第 1 、第 2 、 第 3 应力; σs 为尼龙材料的屈服强度, 取值 60 MPa[12] ; n 为安全应力系数, 取值为 2 。
所以 4 种工况最大应力均满足结构刚性需求, 因此 可对计量盘模型进行减重优化。
3 拓扑优化设计
3.1 优化参数确定
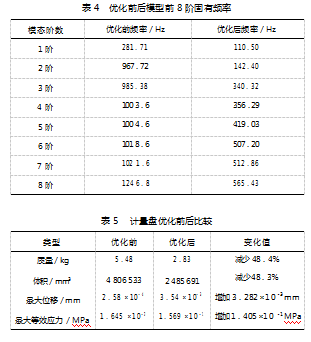
结合上文计量盘模型 4 种工况应力云图可知, 除去 最大应力处所在的非优化区域其余应力分布都集中在计 量盘模型的相同结构区域, 表 3 为工况 1 、4 某同一位置的网格积分点应力值。 由表 3 可知, 两种工况下相同位置网格积分点应力值比较接近, 相差最大值为 0.001 5 MPa。结合数据对比结果, 可将工况 1 的优化结果作为标准替代 其他工况来方便模型计算。
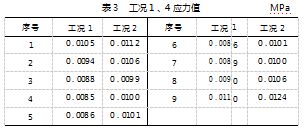
考虑到分析模型载荷的施加方式 、分布区域 、边界 条件位置以及加工难易程度, 需要选定出模型的优化区 域和范围来满足模型制造和应用需求[13] 。将模型所有工 况受力 、边界位置面和其部分连接区域限制为非优化区 域, 模型非优化区域如图 7 所示: 绿色部分为非优化实体区域, 红色部分为冻结表面 ( 后 视 表 面 相 同) 。根据公式 (2) 的数学模型, 以计量盘整体柔顺度为拓扑优化目标函数, 在本研究中目标函数目的是使整体位移最小, 而位移的一个整体度量是模型的应变能, 从而目标函数最终设定为应变能最小。约束条件为减少优化区域初始体积的 30%, 设计变量为单位密度。 设置优化目标函数变化率小于 0.01% 时迭代收敛, 迭代次数 30 次。
3.2 拓扑优化设计
完成优化各项参数设定后开始迭代优化。优化过程 中目标函数和体积变化如图 8 和 9 所示, 当迭代次数等 于 9 时目标函数收敛柔度变化趋于稳定, 同样迭代到第 9 次时体积约束函数收敛, 总体积 减 小 为 初 始 体 积 的 70% 。如图 10 所 示, 计 量 盘 轻 量 化 设 计 效 果 明 显,与工况 1 云 应 力图 比 较, 最 大 Von mises 应 力 值 增 加至 0.157 MPa, 仍满足材料安全系数要求。
拓扑优化得到的模型可能不满足实际工程情况的加工制造要求, 初始拓扑优化结果仍然需要人工处理[14], 如消除孔洞 、形状不规则和复杂边缘并进行人为重构以提高其最终设计制造能力, 修改后最终 的 拓 扑 结 构 如 图 11所示。
3.3 计量盘动态特性分析
模态分析是研究结构动力特性的有效方法, 通过模 态分析, 可以得到一定频率区域内各阶模态的动态特征。 利用 Lanczos 迭代法将计量盘模型转换为有限元模型, 对 于离散无阻尼结构[15] 的振动激励线性运动函数, 在本例 中计量盘模型可以表示为:
M x(··)+ Kx = F (4)
式中: M 为结构质量矩阵 ( 对称矩阵); K 为结构刚度 矩阵 (正定矩阵); x 为节点矢量位移; x(··)为节点加速度 矢量。
由函数方程 (4) 可以得到一个关于 n 阶广义特征值的函数关系式, 其式如下:
( -ω2M + K) 小= 0 (5)
式中: ω为振动频率 ( λ=ω2 ); 小为相关特征向量。
通过 Lanczos 迭代法得到一个三对角 矩 阵, 首 先 选 取一个正交矩阵 Qn = [ q 1. q2. …, qn ], 使得对称矩 阵 M ( n ×n ) 变换成三对角矩阵 Tn, 矩阵方程式:
Q n(T)MQn = Tn (6)
首先进行向量逆迭代, 给定一个初始向量 q1. q1 的 2 范数等于 1 。
K q k+1 = M
对向量正交化:
由计算可知 αi、βi 为三对角矩阵 Tn 的对角元, 对正 交化系数 αi、βi计算:
αi = q i(T)Mqi (9)
βi= q1 Mqi
由上述公式完成迭代形成 m 个正交向量 qi, 由此可得到三对角矩阵 Tm:
「 α1 β1Tm =β1 α2 β2…βm-2αm-1 βm-1βm-1 α 」(10)
求解三对角矩阵 Tm 特征解:
T x = 1 xm i λ i
求解式 (5) 的向量解:
小i = Qm xi i = 1.2.…,m (12)
利用有限元分析软件结合 Lanczos 迭代法计算计量盘 模型优化前后的前 8 阶固有频率, 如表 4 所示。 由表可 知, 优化后的计量盘模型前 8 阶固有频率均有所降低, 但其低阶频率远大于外界激励频率 20 Hz, 避免了共振现象满足模态频率要求。通过表 5 比较, 计量盘的重量比原结构降低 48.4%, 相同静载荷条件下, 优化后模型最 大 Von mises 应力值增大至 0.156 9 MPa, 最大位移增加 至 3.54 ×1 0 -3 mm, 满足刚度要求。
4 结束语
本文以焊条自动计量机构为研究对象, 为达到减轻 焊条箱体重量 、降低电机负载的效果, 对计量盘进行拓 扑优化的同时保证机构性能, 主要完成了两项研究, 结 论如下:
(1) 本文在确定焊条计量盘模型在各工况下满足刚 度要求的条件下, 以计量盘整体柔顺度为目标函数 、减 少 30% 的体积为约束条件, 基于变密度法的拓扑优化理论对计量盘模型进行结构优化。优化结果表明: 计量盘模型重量比原结构减少 48.4%, 在不影响结构性能和完整性的情况下优化了材料整体分布, 轻量化效果比较 明显。
(2) 对人工处理后的优化模型进行模态分析, 计量 盘模型优化后前 8 阶固有频率均有所降低, 外部激励不 能产生共振, 优化模型满足动态特性要求。
参考文献:
[1] 刘金磊,朱南海.基于拓扑优化的 H 型钢梁腹板截面轻量化 设计[J].应用力学学报,2021.38(06):2275-2283.
[2]Aulig N,Nutwell E,Menzel S,et al.Preference-based topologyoptimization for vehicle concept design with concurrent static andcrash load cases [ J ]. Structural and Multipaneliplinary Optimization,2018.57(1):251-266.
[3]郑伟光,陈姗姗,许恩永,等.Helmholtz PDE 敏度过滤技术的 阻尼层拓扑优化 设 计 [ J].机 械 设 计 与 制 造,2022 ( 04 ) : 142-145.
[4]焦洪宇,周奇才,吴青龙,等.桥式起重机箱型主梁周期性拓 扑优化设计[J].机械工程学报,2014.50(23):134-139.
[5]李英磊,曹宗杰.基于变密度法的某飞机隔框结构拓扑优化 [J].计算机应用,2018.38(S1):232-235.
[ 6 ] Niu F,Xu S,Cheng G. A general formulation of structural topology optimization for maximizing structural stiffness [ J ].
Structural and Multidisciplinary Optimization,2011.43 ( 4 ):561-572.
[7] Wang Y,Wang Z,Xia Z,et al. Structural design optimization using isogeometric analysis: a comprehensive review [ J ].
Computer Modeling in Engineering & Sciences,2018.117 (3 ):455-507.
[8]王雨,王勇,陆铭.高速集装箱平车底架结构优化设计[ J].机 械制造与 自动化,2022.51(02):12-15.
[9]张威.基于变密度法的无人机后机身拓扑优化设计[ D].哈 尔滨:哈尔滨工业大学,2020.
[10]程斌,王惠源.气体炮尼龙弹带设计有限元分析[ J].兵器装 备工程学报,2019.40(03):43-46.
[11]邵佳杰,李顺才,喻秋,等.PA6 材料拉-扭组合的力学特征及 屈服准则的试验研究[J].塑料科技,2019.47(06):23-28.
[12]蔡玄龙.钢/尼龙夹层板抗冲击性能研究[ D].镇江:江苏科 技大学,2017.
[13]Yao P,Zhou K,Lin Y,et al.Light-weight topological optimization for upper arm of an industrial welding robot [J].Metals,2019.9 (9):1020.
[14] Manios S E,Lagaros N D,Nassiopoulos E. Nested topology optimization methodology for designing two-wheel chassis [ J]. Frontiers in Built Environment,2019.5:34.
[15]Pang T Y,Fard M.Reverse engineering and topology optimization for weight-reduction of a bell-crank [ J].Applied Sciences, 2020.10(23):8568.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/56452.html