SCI论文(www.lunwensci.com)
摘 要: 介绍了教学团队在线性代数课程中开展“问题 (Problem)— 渗透(Infiltration)— 构思(Conception)— 应用(Applicat -ion)”(PICP)方法的教学思路和体会。通过实践表明:此方法能 助力于学生对大学学习方法的改进和教学内容的消化理解, 提升抽象思辩能力和创新意识,为后续课程的学习奠定基础。
关键词: 线性代数课程,教学方式,PICA 方法,应用型,高校
一、引言
高校经管类专业的专业基础课系列中《线性代数》是本科一年级的主干课程之一,也是后续专业课程的重要理论基础。 线性代数课程内容抽象程度高,理论体系复杂,一直是公认的教学难度较大的课程[1] 。就一年级的新生而言,对大学的生活特点、学习方式和人文氛围原本就存在着亟待适应的过程,加之缺乏线性代数理论知识背后的物理 、几何等其他应用学科背景,所以想要理解线性代数课程的基本理论、基本方法和掌握课程的应用手段都是不太现实的 。而从教育者方面而言,传 统课堂从出现开始,便一直沿用至今,尽管这些年有了不小的变化, 但教学模式一直未有根本性的转变 。一般教科书中的 “定义— 引理—证明—定理—证明—推论”模式对于大多数学生来说是糟糕的体验 [2] 。在高等教育教学改革日新月异的当 下, 国内应用型大学都在针对本校的办学定位和人才培养目标, 对包括数学在内的专业基础课程的教学改革投入了大量 精力和资源,但对于教学效果的影响,却鲜有显著成效 。 目前, 传统的以课堂为主的教学模式还存在着以下一些突出的问题:第一,传统教学模式虽适合于大众教育,但很难根据学生 的自身条件与能力、进行分类或个性化培养;第二,传统教学模式忽略学生自主进行深层学习, 注重的是浅层认知维度的 学习,当学生真正进行思考、动手实践的时候,教师往往不习惯或无法为学生进行较好的引导与帮助;第三,传统教学模式 多数属于以教师为中心的填鸭式教学,学生是被动接受知识。 这类的教学模式易让学生获得了知识, 却可能失去了独立思 考的空间以及创造性思维 。 因此, 要实现教学质量的显著提 升,需要结合学生的实际,更大程度地去更新现有教学方法及 原始的教学模式, 期待任课教师们都能清晰地认识到教学方 法和教学手段改革的重要性及迫切性, 努力地投入并笃定地 参与教学改革的实践和探索, 进而关于线性代数的教学研究 一直是活跃的[3]。
这些年来,我们教学团队针对民办高校的特点以及学校新 生学习基础的实际,秉承着“以教师为主导、以学生为主体、以 能力为本位”的教学理念,充分认识到《线性代数》课程的教学 作为公共基础课在高校教学整体范围的地位和作用, 不断探索和把握本课程的“服务性”“工具性”和“应用性”特色,探究精细拿捏“够用 为度”的衡量尺度的内沿和外延,立足于线性代数课程教学方法的探索和实 践。在课堂教学过程中教学团队不断尝试着“问题(Problem)—渗透(Infiltration)—构 思 (Conception)—应 用 (Application)”(PICA)方法的教学实践并获得了一些成效和教学感悟。
二、课堂教学中 PICA 方法的解释、 实践及案例分析
本文所叙述的“PICA”教学法,即为 将问题看作是课堂教学的动力 、起点和贯穿教学过程的主线, 通过教学来生成问题,把教学过程看成是发现问题、提出问题、 分析问题和解决问题的过程,通过教师的课堂主导和努力促使 学生通过主动学习而积极尝试去解决问题,从中构建以培养学 生的独立思考、主动探研、自觉实践为基本价值取向的教学内 容和教学方法体系[4]。
( 一)问题(Problem)导向为课程设计的主线
本文所表达的“问题”,即为线性代数课程内的数学问题。 线性代数课程的知识构架大多属纯数学理论范畴, 而且它基 本无法借助实验手段(指真正意义上的实验过程)通常只能仰 仗学习者独立思考来完成整个学习过程 。学习的过程就是学 生不断认知、逐步促使知识的消化及吸纳的过程 。而知识的获 取是人们根据现有的理论来建构科学知识, 强调科学知识是 暂时的、主观的、建构性的,它会不断地被更新和推翻 。从认知 的视角观察, 不同的人对同一个知识建构的认识通常是不尽 相同的,但都必须经历“发现认知窗口”的路径—— 发现问题。 从宏观的角度俯视线性代数课程全貌, 可以毫不夸张地说此 课程就是由成千上万个大小不一、表现形式各异、深浅程度不 同的数学问题串联或并联而成的 。有些问题是表象易见的,而 有些问题往往会隐蔽在某些不易察觉的角落, 它们为学生的 学习过程埋下了困难的伏笔 。所以,我们认为以问题为导向的 教学是线性代数课程教学设计的主线和抓手。
1.教师提出问题及引导学生发现问题是课程教学的要务 。 由于高考指挥棒的驱使和众所周知的缘故, 高中数学的教学 往往更重视及强调学生解题能力的造就和提升, 教师常常在 不自觉中忽略了对课本内容基本结构的深层次探究和把握 , 淡化了学生对提出问题 、分析问题和解决问题等基本能力的 培养 。而进入大学后,学生一旦接触到类似于线性代数这种理 论性强,概念抽象的课程,往往会感觉不适 。这就要求教师们 在教学活动中除了责任心和耐心外, 还需结合学生的实际注 重教学方法的应变及运用 。本教学团队在集体备课中运用了 将线性代数课程各个章节实施课题引入—— 内容展开—— 理 论推导—— 范例演绎—结论表述等程序化流程并将教学环 节都以“问题”的形式铺开,在问题的设计中注重密切关注两 个关键点:一是处理好知识点与问题之间的关系,尽量将诸多 知识点分解为问题的公开和问题的解决两个部分—— 知识点 始于问题的披露而终于问题的化解 。这样的益处是通过潜移 默化的教学,使学生们能将知识点与问题一一对应,便于记忆 和理解,如图 1 。二是在编辑问题时不仅需紧贴教学内容设计 出具有主导性、启发的问题——从教师对本章节教学构思的角 度出发,结合教材、配合教案、开启学智,构建充分体现教师在 教学中主导作用的问题,譬如富有“拨云见日”特性的主旨性 问题;具有“四两拨千斤”特征的核心性问题;具有“指点迷津” 特质的启发性问题等; 而且更需要通过各种教学手段诱发学生积极思考,发现并提出自己的问题,即使学生提出的问题可 能比较幼稚甚至是“伪”问题,但这确是我们谋求学生在教学 中发挥主体作用的切入口, 是激发学生参与课堂教学的良好 开端,更是难能可贵的教学实效。

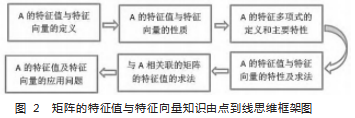
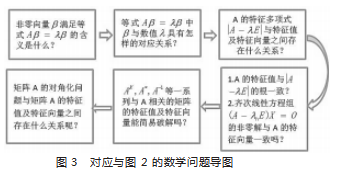
2. 问题与教学内容的契合关系 。每个数学任课教师都明 白,我们的课堂教学不能仅仅停留在讲清单一 的基本概念,还 需厘清相关内容之间的理论脉络, 提炼出隐藏在知识点背后 深层次的数学思想, 这对学生数学素养的提高无疑是很有意 义的[4] 。因此,在问题的设计中,我们教学团队除了关注知识点 与问题的联系, 还精心探究同一章节内众多知识点前后的逻 辑关系,通过诸多个问题的引导,凸显出知识群的基本理论脉 络, 进而促使单 一 章节知识领域中 (知识) 点—— (知识) 线—— (知识)面的有机复合 。这里特别强调的是,由点到线的 形成关键是它们的“逻辑性”,即若干彼此富有逻辑内在联系 的知识点才可能汇成一个知识群(线) 。为了表达得更清晰,现 以矩阵 A 的特征值与特征向量的教学内容为例。
设 A 为一个 n 阶方阵, 于是我们用图 2 及图 3 表述由点 到线的知识点思维逻辑框架图和相应的数学问题导图:
教学建议:为使学生在新教学模式中能迅速进入角色,根 据课程要求和学生实际,教师应该在课前做足准备,譬如拟定 内容对象制作问题 、各类问题的表述方式, 选编典型问题案 例、预设学生的提问及应答等等 。进入课堂教学后,教师还可 进一步(例如通过多媒体和网络手段)充实问题案例的背景, 使学生在问题案例的情景中产生感性认知。
一般而言,由于基础知识 、数学功底 、抽象思维能力和表 达水平等不同因素的影响,学生会不时地“大胆”抛出一些伪 问题,而且往往认为自己的结论是正确的 。此时教师可以凭借 教学经验和专业敏感捕捉这些极具典型案例意义的素材,指 出问题自身的症结并加以校正; 同时在避免伤害学生自尊的 前提下, 从多视角揭示形成无效问题的专业知识背景和事物 认知背景, 使纠错的过程演变成激发学生加速提升自身分析 能力、感知能力和解决问题能力的孵化器。
(二)数学思想的渗透(Infiltration)是课程教学的硬核
恩格斯曾说过:数学上的所谓公理,是数学需要用作自己 出发点的少数思想上的规定 。公理化思想及方法发展源于亚 里斯多德的完全三段论及欧几里得《几何原理》的问世[5]。事实 上在基础教育阶段,学生们都曾接触过类似于“两点之间直线 距离最短”这样的数学公理,但在大学的理工类课程里,层出 不穷的公理化问题集中涌现在同一 门课程里,恐怕只唯《线性 代数》莫属了。譬如行列式的构造、矩阵及矩阵的运算、向量组 的线性相关性、二次型标准化问题等等 。最典型的当属向量空 间系统:当人们分别研究了许多具体的空间结构以后,发现了 它们具有基本的共同属性, 于是就用满足一定条件的公理集 合来定义向量空间(俗称三大条八小条),形成一个向量空间 的公理系统, 并在这个系统上展开空间的理论并推导出一 系 列定理 。我们很容易发现,这种能反映公理化思想的范例毫不 夸张地说在教材中可以随手拈来 。公理化思想和方法能系统 地总结数学知识、清楚地揭示数学的理论基础,有利于比较各 个数学分支的本质差异,是现代科学发展的基本特点之一 。鉴 于本课程的这一特点以及新生还陷于探求和熟悉学习环境的 特殊时期,无论是数学知识的特性还是学习方法的掌握,他们 都会不太适应,故任课教师需尤其给予高度关注,如何才能使 得学生尽早地适应课程知识构造特点, 如何通过课堂教学促 使学生逐渐领会及感知“公理化”的数学思想,是鉴别我们的 课堂教学工作成效的标志之一。
教学建议:教学实践告诉我们,由于《线性代数》的概念众 多而繁杂,学生往往会不知所措 。因此,我们有责任告诫并引 导学生:课程的学习不仅仅是搜集信息和概念,也不是一大堆 事实及材料的简单积累, 这些教学内容都有其自身的出发点 和符合一定规则的逻辑体系[6] 。同时,教师的重要职责就是帮 助他们抽丝剥茧, 利用公理化思路以及恰当的方式方法建立 起各个章节的教学内容逻辑体系。
(三)学习方法构思(Conception)的养成是课程教学的责任
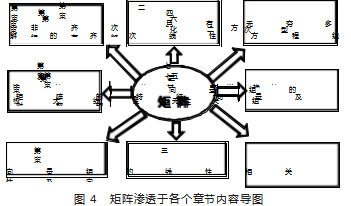
1.数学思想方法的构思。数学思想方法是数学思想和数学 方法的概况 。如果说数学思想是长期实践而形成的对数学的 理性认识,是解决数学问题的根本要素,那么数学方法就是解 决数学问题的手段和工具 。可以这样认为:数学思想方法彰显 的是数学的灵魂,只有当明确和把握了数学思想方法,才算正 真掌握了数学 。因限于篇幅, 本文只讨论数学方法构思的问 题 。笔者认为线性代数课程教学中,除了应注意促使学生了解 和领会分类探究方法 、化归与转化方法等一般性常见的学习 技巧外, 此文特别地结合线性代数课程的特点着力推荐用途 更为广泛的“矩阵主导”的方法。
所谓的“矩阵主导”是指以矩阵为重要媒介和计算工具, 介入及参与线性代数课程其他主要章节的学习内容过程的表 现手法及方法 。事实上,在整个课程学习过程中,我们很容易发现矩阵真可谓无处不在(除了行列式之章节),这是由于它总体处于课程的核心地位,并形成各章知识前后联系的纽带,就犹如一条红线从头至尾贯穿于课程始终 。所以有专家戏称:抓住了矩阵,就套牢了线性代数课程的“牛鼻子”。因此,每一位任课教师都需要高度重视矩阵本身的结构和性质, 以及矩阵在各个章节内置的特殊作用 。矩阵的概念在其它章节的哪些具体内容中发挥作用,我们可以通过图 4 给予部分说明。
2. 计算方法的构思 。线性代数课程的教学除了基本概念外,更多地是涉及有关计算方法的问题 。由于课程中对应的数学对象相异,相应的计算方法也不尽相同,这往往会给学生带来一些解题思路上的混淆和学习方法上的错位 。为了避免上述现象,笔者认为任课教师可能需要关注以下两个教学环节。首先,在每类计算方法引入当初,需要“细嚼慢咽”,扎实学生的基本功,力争在学生脑海里打下深刻烙印;其次,对庞杂的各种计算方法进行必要的细分对比,总结归纳(往往容易忽视这点) 。本文利用图 5 给予提示。
事实上,一个教学单元内容结束后,有条理地进行一次计 算方法的梳理和归纳,对学生消化知识,巩固知识都是一件事 半功倍的工作,尤其在强化学生对诸多方法的理解 、记忆 、消 化和“构思”,能起到很好的作用。
3.证明方法的构思。因受到教学课时及教学目标的限制及 约束,线性代数课程中的定理证明、证明式习题等有关开放性 主观问题的训练也许不会作为主要教学内容, 但不可否认的 是,数学证明不仅是数学发展的推动力之一,更是大学阶段学 生理性智力开发的重要途径 。尽管数学的证明过程技巧性极 强,涉及的概念和知识点颇多,而且数学问题的证明讲解也因 难以把握而容易造成学生悲观及厌学情绪的产生, 但我们也 绝不能放弃 。在通常情况下,教师可以设计出多种教学手段和 方法处理这个 。本教学团队曾使用过如下方法,促进学生的解 题构思: 对数学问题给予必要的分析并摒弃错误的技术路 线—— 构架问题证明的步 骤—— 明示证明过程的细节和方 法—— 给予必要的提醒和补充——设计类似的问题激励学生 进行尝试等等 。通过训练带来了不错的效果,实践证明只要工 作到位, 通常我们还是有信心唤醒学生的自信和接受挑战的 勇气的 。下面就以一道数学证明题的解题过程及图 6 呈现我 们的教学设计。
数学问题:设 m1.m2.L,m3 是非齐次线性方程组 AX=b 的解, 而 k1.k2.L,ks 是满足等式 k1+k2+L+ks=1 的一组实数, 证明: m=k1 m1+k2 m2+L+ks ms 为原线性方程组 AX=b 的解。
预备工作:简称原方程组 AX=b 为①;解题目标:设法推出 结果 Am=b;必要提醒:非齐次线性方程组解的线性组合未必 还是原方程组的解。
( 四)数学知识的应用(Application)是课程教学的 目标
如何培养和开发学生的数学思想,始终是数学教育工作者 普遍关注和潜心探究的一项重要课题,就线性代数课程而言, 学生能否利用所学的数学知识应用到实践中并解决数学问 题,即会不会应用、应用得好不好,这既是检验学生掌握课程 基本知识及数学思想的重要标准,也是数学教学所追求的根本 目标 。线性代数课程知识的应用问题主要是通过课堂例题、课 间训练和课后习题来付诸实施,所以课堂习题训练及课后作业 演练一直是任课教师高度重视的教学环节 。建构主义“学习环 境”理论认为,学习者的知识储备往往是借助他人的帮助,通 过意义建构而逐步获得, 我们团队在上述环节的实践中获得 如下体验,教学活动中最好能关注下面几个问题:
1.建构学习情境 。在教学设计中,创设有利于学生投入习 题训练的情境是不能忽视的 。比如习题课堂热烈的氛围、争先 恐后展示训练结果的积极性、对不同解题方法踊跃提出自己主 张的勇气,解题过程的讨论和兴趣能延伸至课后等等。
2.建构协作精神。学习协作精神的培养和建立既是班风的 重要组成部分,也是习题演练课堂提升效率的恒久动力 。这种 精神可以产生于师生之间也可体现在学生群体之中,比如学习 进程的自我反馈和学习成效的评价、学习资料的收集与分析和 假设的提出与验证等,应该贯穿于整个学习活动过程之中。
3.建构交流习惯。师生之间和学生之间的学习交流事实上 是协作过程的一种最基本的方式 。为了便于开展交流,我们成 立了多个班级学习小组,建立了班级微信学习群,制定了定时 和不定期的学习交流制度 。尤其是任课教师时常录制一些课外 补充内容及习题训练短视频投放到群里交流共享, 对推进学 习进程和改进认知状况起到了很好的作用也深受学生的认同。
三、结语
近年来,教学团队在专业基础课《线性代数》教学过程中不 断地汲取教训及总结经验,在摸索中探究出“问题(Problem)— 渗 透 (Infiltration)—构 思 (Conception)—应 用 (Application)”(PICA) 方法,收到了一定的成效和感悟,同时也意识到日后继续改良 和提升的方向 。上述 PICA 方法基本适应于线性代数课程的大 部分概念和理论的教学, 但也可结合具体实际进行必要的调 整,比如其中四个取项的有机融合、先后次序的置换和选项的 取舍等 。值得提醒的是在采用本方法时任课教师需要做足课 前的准备,除了正常的传统备课,兴许还要在教学案例 、数学 问题、思路导图等多方面进行前期设计和研制 。当然,大学公 共基础课通常还包括大学英语、政治思想理论课 、大学语文 、 大学应用文写作,体育和艺术领域的诸多课程,希望本文能从 课程教法的角度为上述课程教学改革提供些许参考或借鉴 。 我们认为无论课程的构架和内涵如何不同, 只要秉承进取之 心,不断探索教学规律,总能挖掘和开创出符合课程规律的教 学改革之果 。教学方法和教学手段的改革是永无止境的,但始 终会遵循众所皆知的客观规律:一份耕耘,一份收获。
[基金项目:2018 年广西外国语重点课程(高等数学)及数 学应用与数量经济教学团队建设校级项目 。
参考文献:
[ 1] J.M .Day, D .Kalman.Teaching Linear Algebra: What are theQuestions [EB/OL].Availableat:http//wwwl.american.edu/academic . depts/cas/mathstat/People/kalman/pdffiles/questions.pdf.
[2] F.Uhlig.The Role of Proof in Comprehending and Teaching Elementary Linear Algebra [J].Educational Studies in Mathematics,2002.50 (03):335-346 .
[3] J.L .Dorier et al .On a research programmer concerning the teaching and learning of linear algebra in the first-year of a French science University [J].INT.J.MATH.EDUC. SCI . TECHNOL,2000.31 (01):27-35 .
[4] 任北上,刘立明,李碧荣 . 问题型教学模式在高等代数教学中 的探索[J].数学教育学报,2013( 02):95-98.
[5] 王光明 .数学教育研究方法与论文写作[M]. 北京:北京师范大 学出版社,2010.
[6] 邓勇,吴宏 . 线性代数课程教学的探索与实践[J].数学教育学 报,2012.21( 02):74-77.
(作者单位:广西外国语学院 广西南宁 530222)
[作者简介:韦玉球,副教授,研究生学历,研究方向:数学教育及 师培 。]
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jingjilunwen/62633.html