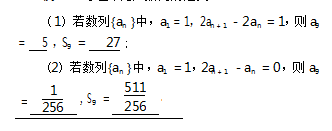SCI论文(www.lunwensci.com)
摘 要 : 高考中数列模块是“兵家”必争之地.其中等差数列与等比数列的基本概念、常用公 式、简单性质、基本运算最为重要.难度不高,却也灵活.能否迅速且高效、准确、熟练地掌握它们的 运算特征,是否懂得选择简便的解法成为复习的关键.
关键词 : 数列,等差,等比,核心素养,运算求解
数列无疑是现今各版高考卷的重点,在新高考 Ⅰ卷中考查地位稳定,难度不高,一大一小.主要考 查等差数列与等比数列的基本运算及性质.主要涉 及运算求解的数学核心素养,以及化归转化的数学 思想方法.
等差数列与等 比数列在定义、知识 点、公式、 性质、运算上既有相同点又有明显的区别,宜放 在一起类 比进行 复 习.本文一 比 到底,简 明扼要 地展示这些同与不 同,帮助大家更深刻地领会这 两种特殊的数列.
1 基础易错
例 1 等差( 比) 数列的定义.
设计意图 等差( 比) 数列的定义是一种特殊 的递推关系式,通过运算变形,把“不标准”的递推 公式化为“标准”的定义,使同学们掌握等差( 比) 数列定义.
例 2 等差( 比) 中项.
( 1) 已知三个数 x -1.2x -2.x 成等差数列,则 x=3/2.
(2) 已知三个数 x -1.2x -2.x 成等比数列,则 x=4/3.
设计意图 第(2) 题你错了吗? 三个数成等差( 比) 是最小单元的等差( 比) 数列,最是寻常,不容 有误.要注意 : ①等比数列不能有 0 项 ; ②“a,G,b 成 等比数列”是“G2 = ab”的充分不必要条件,所以算 出来要验证,而三个数成等差的情况下算出来不用验证,为什么呢?
例 3 已知方程 x2 + 10x + 16 = 0.
( 1) 等差数列{an }中,a1 与 a9 是这个方程的两 根,则 a2 + a8 = -10 ,a5 = -5 ;
(2) 等比数列{an }中,a1 与 a9 是这个方程的两 根,则 a2 · a8 = 16 ,a5 = -4 .
设计意图 求出根的解法不如用“性质 + 韦达 定理”的解法,性质如 : 等差数列中有 a1 + a9 = a2 + a8 = … = 2a5 ,等比数列中有 a1 · a9 = a2 · a8 = … =a5(2) ; 第( 2 ) 题 易错,需知等比数列的符号规律 : 奇(偶) 数项同号,为什么呢?
2 解法多样
例 4 已知数列{an }中,a1 + a3 + a5 = 9.a2 + a4+ a6 = 18.
( 1) 若{an }是等差数列,则公差 d = 3 ,首项 a1 = -3 ;
(2) 若{an }是等比数列,则公比 q = 2 ,首项 a1 =3/7
设计意图 典型运算,( 1 ) 中左减左等于右减 右,(2) 中左除以左等于右除以右,两种数列运算区 别明显.等差数列的项与项是和差关系,等比数列的 项与项是倍除关系.此题用通项公式解最慢,( 1) 中 用性质也行,利用项与项的关系解题最快,注意体会,注意观察下标.
3 典型必刷
例 7 等差中有等比,等比中有等差.
4 类比延伸
以上遴选 12 例,基础的、易错的、典型的、延伸 的,覆盖了等差( 比) 数列的主要方面,通过对比的 方式寻微探幽、夯实基础,使学生深刻体会这两种特 殊数列的基本运算特征,把数学运算的核心素养落 实到位.
参考文献 :
[1]任晓松.关注生之误 谋划教之变[J].数学通 报,2020.59(10) : 58-61 .
[2]柴有茂.核心素养引领下的“等比数列”教学设 计[J]. 当 代 教 育 与 文 化,2018.10 ( 03 ) :85-88 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/71475.html