SCI论文(www.lunwensci.com)
摘 要 : 本文依托梅涅劳斯定理,探究有一条公共边的两个三角形拼接到一起,两条截线相交, 且交点落在公共边所在直线上,线段之间会有怎样的比例关系.
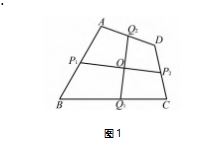
“田”字格是一种常见图形,它普遍存在于凸四 边形之中.例如凸四边形 ABCD 中,点 P1.P2 分别为对边 AB,CD 上的点,点 Q1.Q2 为另一组对边 BC,AD 上的点,P1 P2 与 Q1 Q2 交于点 O,( 如图 1 ),田字 格就是指这类图形,图中包含了三对横向线段AQ2. Q2 D,P1 O,OP2.BQ1.Q1 C,三对纵向线段 AP1.P1 B, DP2.P2 C,Q2 O,OQ1.本文所说的“田”格等比定理就 是以这几对线段成等比关系作为条件或作为结论的 定理,如未特别说明,文中的四边形是指平面上的凸 四边形.
1 接受启发,雏形初现
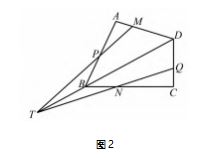
如图 2 所示,有一条公共边的两个三角形拼接 到一起,两条截线相交,且交点落在公共边所在直线 上,线段之间会有怎样的比例关系,实际上问题来到了四边形中,进而又想到了图 1 中的“田”字格.
受到梅涅劳斯定理的启发,发现下面的问题 :
问题 1 若 M,N 是四边形 ABCD 的边 AD,BC 上的两点,T 为直线 BD 上的点,直线 MT 交 AB 于点
4 打铁还需自身硬
师者,所以传道授业解惑也.作为一名中学数学 教师,要提升学生的数学核心素养,自身必须扎实过 硬和技高一筹,而定理的发现一般是经历严密的逻 辑推理过程,甚至是曲折且漫长,但长期的坚持不懈 定能助长学生的推理习惯,本文就是将田格等比定 理的生成过程详尽阐述并展现.大家知道逻辑推理 能力的提升更是核心素养培育的任务之一,希望更 多师者投身到研究中来,努力提升自身的核心素养.
参考文献 :
[1] 王庆龙.知识交汇巧设置,问题解决显身手——— 以解三角形为例 [J].中学数学,2018(11) :47-49.
[2] 高军.聚焦多维探究 渗透数学思想——— 一道三角形面积最值问题的探究及教学思考 [J].福 建中学数学,2021 (03) : 35-38.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/66231.html