SCI论文(www.lunwensci.com)
摘要:关于ex、lnx、x的组合函数问题,按常规方法解答难度较大.如果能抓住组合函数的结构特征,合理构造新函数,可以将问题转化为常见的超越函数问题.2022年高考甲卷第22题至少可以用两种不同的构造法来解答.
关键词:构造,导数,研究
1题目再现
题目(2022年全国高考甲卷第22题)已知函数f(x)=
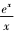
-lnx+x-a.
(1)若f(x)=0,求a的取值范围;
(2)证明:若f(x)有两个零点x1,x2,则x1 x2<1.
2总体把握
本题题设简洁,问题常规.第一问模式近十年来经常考查,本质是求函数的最小值,进而得出参数范围.可以直接求最小值,也可以分离参数构造函数求最值,还可以指数与对数相互转化构造函数求最值.第二问属于典型的极值点偏移问题,有很多办法可以处理它,由于问题有高数背景,并不容易解答.紧紧扣住已知函数的结构,指数与对数相互转化构造函数相对容易一些.
3解法探究
3.1常规解法
分析1对于(1),利用教材知识:用导数研究函数的单调性、极值、最值,按部就班可以解答,在求导过程中,注意因式分解,将超越式转换为整式或分式,基本功扎实的学生还是可以完成的.
对于(2),直接作答,思路不畅,方向不明,我们如下图所示
构造法解题显得很便捷,使用也非常广泛,在三角、数列、函数、导数、解析几何、立体几何、解不等式中均有应用.在平常学习中应注意积累,在结构上下功夫,提高应用意识,主动探究构造路径,一些问题构造方法较多,如本题.通过本题的对比解答,不难看出构造法的妙处,通过长期主动训练,一定能提高我们的创新水准.
参考文献:
[1]胡贵平.指对同构法处理导数题[J].数理化解题研究,2021(01):30-32.
[2]符强如.着眼基础回归教材———2019年全国Ⅱ卷第22题解析与思考[J].理科考试研究,2020,27(03):15-17.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/70417.html
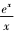 -lnx+x-a.
-lnx+x-a.