SCI论文(www.lunwensci.com):
摘要:从构造函数与减元的角度给出2022年高考甲卷导数压轴题的多种解法,并给出该考题的变式以及考题溯源.
关键词:2022年数学高考;导数题;一题多解;考题溯源
1试题呈现
试题(2022年高考全国甲卷21题)已知函数
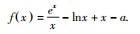
(1)若f(x)≥0,求a的取值范围;
(2)若f(x)有两个零点x1,x2,求证:x1 x2<1.
2试题分析
这道题综合考查利用导数研究函数的最值,再利用单调性与极值求给定条件下参数的取值范围,在此基础上研究两个零点之间的关系,是典型的极值点偏移问题.试题起点较低,绝大多数学生都可以拿分,但落点很高,第二问难度大,需要考生熟练掌握函数的有关性质,以及研究有关性质的基本方法和工具,并达到灵活运用的程度.对数学思想方法的考查也占很大成份,特别是对分类计论思想和转化思想的要求很高,只会死记硬背、按套路做题不会变通的考生是做不下去的.
极值点偏移问题的解题大方向主要有两个:构造对称函数和减少变量转化为一元函数问题.
3解法探究
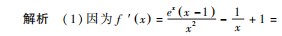

所以f(x)在(0,1)内单调递减,在(1,+∞)内单调递增,则f(x)min=f(1)=e+1-a.因为f(x)≥0⇔f(x)min≥0,所以e+1-a≥0,
得a≤e+1.
故a的取值范围为(-∞,e+1].
(2)由(1)知f(x)有两个零点的条件是a>e+1,且在(0,1)和(1,+∞)内各有一个零点,不妨设0 < x1 < 1 < x2 .
下面证明:当 x > 1 时,ex > ex.
设 s( x ) = ex - ex, x > 1,则 s′( x ) = ex - e > 0.
所以 s( x )在(1, + ∞ )内单调递增. 故 s( x ) > s(1 ) = 0,ex > ex 得证.
于是 xe 1x + 1 - ex - x < ex + 1 - ex - x = 1 - x < 0.
所以 g′( x ) < 0. 则 g ( x )在(1, + ∞ )内单调递减.
以下同解法 1.
方法 3 (利用同构化简,再构造函数)
点评极值点偏移问题主要有两种基本类型,即x1 x2大于(或小于)常数a,以及x1+x2大于(或
小于)常数a.构造函数 是解这类题的一种常用方法,这种解法的目的是得到不等式
是解这类题的一种常用方法,这种解法的目的是得到不等式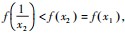 再利用f(x)的单调性,得到与x1的大小关系.上面五种解法代表了解极值点偏移问题的两种常见方法:前三种方法是构造对称函数,后两种方法是利用消元、换元或对数平均不等式转化为一元函数问题.只有理解这两种方向解法的思维过程和基本方法,才能应对可能出现的各种变化,真正做到随机应变.当然,在实际运用中还需要根据具体情况灵活处理,有时甚至还要对解题方法作一定的变通,活学活用才是最重要的.
再利用f(x)的单调性,得到与x1的大小关系.上面五种解法代表了解极值点偏移问题的两种常见方法:前三种方法是构造对称函数,后两种方法是利用消元、换元或对数平均不等式转化为一元函数问题.只有理解这两种方向解法的思维过程和基本方法,才能应对可能出现的各种变化,真正做到随机应变.当然,在实际运用中还需要根据具体情况灵活处理,有时甚至还要对解题方法作一定的变通,活学活用才是最重要的.
4变式
问题等价于证明:
5考题溯源
溯源1(2021年新高考Ⅰ卷)已知函数f(x)=x(1-lnx).
(1)讨论f(x)的单调性;
(2)设a,b为两个不相等的正数,且blna-alnb
=a-b,证明:
分析(1)f(x)的单调增区间为(0,1),单调减区间为(1,+∞).
(2)由(1)知f(x)在(0,1]上单调递增且limf(x)=0,在(1,+∞)上单调递减且f(e)=0,x→0+f(x)≤f(1)=1.
则问题等价于证明:2 < x1 + x2 < e
通过构造函数g(x) = f(2 - x) - f( x) (0 < x <1),再结合g(x)的单调递减即可证明,类似可证x1+x2<e.
本题属于典型的极值点偏移问题,构造函数即可证明.
溯源2(2018年全国Ⅰ卷)已知
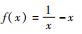 +alnx.
+alnx.
(1)讨论f(x)的单调性;
参考文献:
[1]邓启龙.函数极值点偏移和拐点偏移问题的探究[J].数理化解题研究,2022(13):37-39.
[2]黄小妹.如何破解极值点偏移问题[J].数理化解题研究,2021(04):7-8.
[3]李鸿昌.一道新高考导数压轴题的解法探究[J].高中数学教与学,2021(15):22-23.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/43911.html
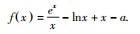

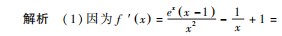
 所以f(x)在(0,1)内单调递减,在(1,+∞)内单调递增,则f(x)min=f(1)=e+1-a.因为f(x)≥0⇔f(x)min≥0,所以e+1-a≥0,得a≤e+1.
所以f(x)在(0,1)内单调递减,在(1,+∞)内单调递增,则f(x)min=f(1)=e+1-a.因为f(x)≥0⇔f(x)min≥0,所以e+1-a≥0,得a≤e+1.


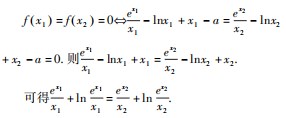


 是解这类题的一种常用方法,这种解法的目的是得到不等式
是解这类题的一种常用方法,这种解法的目的是得到不等式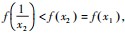 再利用f(x)的单调性,得到与x1的大小关系.上面五种解法代表了解极值点偏移问题的两种常见方法:前三种方法是构造对称函数,后两种方法是利用消元、换元或对数平均不等式转化为一元函数问题.只有理解这两种方向解法的思维过程和基本方法,才能应对可能出现的各种变化,真正做到随机应变.当然,在实际运用中还需要根据具体情况灵活处理,有时甚至还要对解题方法作一定的变通,活学活用才是最重要的.
再利用f(x)的单调性,得到与x1的大小关系.上面五种解法代表了解极值点偏移问题的两种常见方法:前三种方法是构造对称函数,后两种方法是利用消元、换元或对数平均不等式转化为一元函数问题.只有理解这两种方向解法的思维过程和基本方法,才能应对可能出现的各种变化,真正做到随机应变.当然,在实际运用中还需要根据具体情况灵活处理,有时甚至还要对解题方法作一定的变通,活学活用才是最重要的.


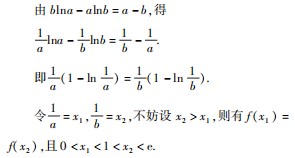
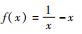 +alnx.
+alnx.
