例谈利用基本不等式求最值常见错解剖析论文

SCI论文（www.lunwensci.com）

　　摘要:基本不等式是高中数学重要内容，也是历年高考的重点之一．基本不等式成立的条件是“一正、二定、三相等”，利用基本不等式求函数最值时，学生常因忽视条件而出现一些错误，针对这种情况，教师若能及时列举错解，让学生辨析，不仅可以强化知识，还能培养学生思维的批判性.

　　关键词:例谈;基本不等式;最值;错解

　　我们把“如果a＞0，b＞0，那么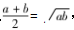，即a+b=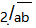(当且仅当a=b取等号)”称为基本不等式，也叫均值不等式．在利用基本(均值)不等式求函数的最值时，必须要同时满足“一正、二定、三相等”这三个条件，三者缺一不可．其中“一正”是指式子各项全为正数;“二定”是指和或积为定值，即若积为定值，则和有最小值，若和为定值，则积有最大值;“三相等”是指满足等号成立的条件，即等号一定能取到．利用基本(均值)不等式求函数的最值时，初学者容易出现这样或那样的错误，下面举例说明，引以为戒.

　　1忽视各项必须均为正数的条件

 

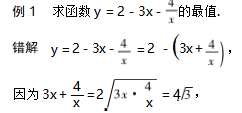
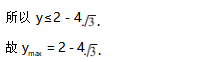
　　错因剖析 上述解法是错误的，错在没有严格区分x＞0还是x＜0的情况下，就盲目地应用均值定理来求解.

 

　　点评 a+b=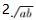成立的条件之一就是a，b为正实数，一定不要忘记.

　　2忽视积或和为定值的条件


 

　　错因剖析 上述解题错误是不等式右边不是常数，不符合基本不等式求最值的条件:和为定值

 

　　点评 利用a+b=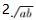求函数的最值必须是积或和为定值．为利用基本不等式时出现定值，先要根据式子的特征进行灵活变形，配凑出积或和为常数的形式.

　　3忽视等号成立的条件


 

　　4多次使用基本不等式，忽视等号成立条件的一致性


 

 

　　点评 在利用基本不等式求最值时，一定要尽量避免多次使用基本不等式，若必须多次使用，则一定要保证它们等号成立的条件一致，否则得到的结果很可能不是要求的最值.

　　总之，利用基本不等式求最值时，对“一正、二定、三相等”这三个条件必须时刻牢记．利用基本不等式求最值关键在于确定“定值”，即凑成“和为定值”或“积为定值”的形式，所以要掌握一些拆项、凑项的技巧.

　　参考文献:

　　［1］汤池武．利用基本不等式求最值问题常见的三个误区［J］．中学生数理化(高二数学)，2020(11):38－39.

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jiaoyulunwen/69779.html