SCI论文(www.lunwensci.com):
摘要:在简要梳理2020年天津卷第14题多视角解答的基础上,揭示了试题命制的高等数学背景,并对试题进行了变式与推广研究,得到了一些有趣的结论.
关键词:拉格朗日乘数法;极值问题;逻辑推理;数学运算
1试题呈现
题目(2020年高考天津卷第14题)已知a>0,
b>0,且ab=1,则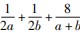 的最小值为.
的最小值为.
本题是二元方程约束条件下的二元函数最值问题,试题设计简洁清新,构思别具匠心,解法灵动多变,饱含数学思想,凝聚命题专家的智慧.同时,试题涉及知识点较多,综合性较强,呈现出一定的综合性与选拔性,需要较高的逻辑推理、数学运算、直观想象等核心素养.
2初等解法
在高中阶段,解决此类问题可从方程有解、函数最值(三角代换或导数)、不等式(如基本不等式、柯西不等式等)等视角解答.其中,消参减元转化是解题的基本原则,即把双变量问题转化为一元函数或方程问题,再辅以转化与化归、函数与方程、分类讨论、换元法、配方法等典型数学思想和方法,妙趣横生.
2.1利用基本不等式
解法1因为a>0,b>0,ab=1,
 令f ′ ( t ) =0,得 t=4.
令f ′ ( t ) =0,得 t=4.
当 0 < t <4 时,f ′ ( t ) <0,f(t )单调递减;
当 t >4 时,f ′ ( t ) >0,f(t )单调递增 ,

 3命制背景
3命制背景
本题命制的背景是拉格朗日乘数法求极值问题.其基本原理是:设给定二元函数z=f(x,y)和附加条件φ(x,y)=0,为寻找z=f(x,y)在附加条件下的极值点,先构造拉格朗日函数L(x,y)=f(x,y)+λφ(x,y),其中λ为参数,求L(x,y)对x,y的一阶偏导数,令它们等于零,并与附加条件联立,即

由上述方程组解出x,y及λ,如此求得的点(x,y)即是函数z=f(x,y)在附加条件φ(x,y)=0下的可能极值点.若这样的点只有一个,可确定此点即为所求的点.
其几何意义是:设给定目标函数为f(x,y),约束条件是φ(x,y)=0.如图1示,曲线L为约束条件
φ(x,y)=0,f(x,y)=C为目标函数的等值线族.在f(x,y),φ(x,y)偏导数都连续的条件下,目标函数f(x,y)在约束条件φ(x,y)=0下的可能极值点M(x0,y0)必是目标函数等值线族中与约束条件曲线的切点.
图1
拉格朗日乘数法的优点有二:一是把目标函数和等式约束统一到一个拉格朗日函数中;二是将条件极值问题转化为无条件极值问题,即通过引入拉格朗日乘数将含有n个变量和k个约束条件的约束优化问题转化为含有n+k个变量的无约束优化问题.另外,L(x,y)=f(x,y)+λφ(x,y),其中φ(x,y)=0,求z=f(x,y)的极值点就是求L(x,y)的极值点,两者的极值是等价的,且与λ无关.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/44210.html
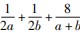 的最小值为.
的最小值为.

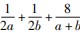 的最小值是 4.
的最小值是 4.





 + 8 ( a + b )的最小值为
+ 8 ( a + b )的最小值为




