SCI论文(www.lunwensci.com)
摘 要: 在漫长的实践经验与认识活动的历程中,人们针对事物的数量关系、空间结构和科学认识综合归纳出数 学分类讨论思想。通过学习基础数学知识、接触不同数学方法和运用基本数学思想, 学生能够了解更多解题方法, 也 能够在学习过程中提高综合运用能力。常用的数学分析思想包括数形结合思想和分类讨论思想,还有函数与方程 思想、等效思想等。文章指出,分类讨论法的运用有助于学生提高数学解题能力,为后续学习奠定良好的基础。
分类讨论法作为初中阶段应用较多的教学方法, 是 数学思想的具体体现,也是数学课堂的教学重点 [1] 。 帮助学生在分类讨论教学活动中学习教学知识,是教 师可以采取的一种教学方法,也是教师在教学中的创 新。二次函数是函数知识学习的基础。笔者结合自身 教学实践经验,对分类讨论法在初中数学二次函数 教学中的应用展开探讨,并结合实际教学案例加以分 析,以供各位读者阅读参考。
一、分类讨论思想在正向型函数教学中的应用
正向型函数是指已知二次函数的定义域及区间, 求 取二次函数的最值。为高效完成这一问题的讲解,教 师可以根据题目中函数对称轴与定义域区间之间的位 置关系组织学生展开分类讨论活动。正向型函数教学 的讨论过程可以分为三个项目,即轴定区间定、轴定 区间动和轴动区间定。
(一)轴定区间定
“轴定区间定”这一情况是指,在已知二次函数 的情况下,根据所给出的固定定义域区间,计算二次 函数在定区间上的最值。
例 1:函数 y=-x2+4x-2 在区间 [0.3] 上的最大值 和最小值分别是多少?
首先,教师可引导学生根据所给出的函数进行简 化,要求学生将题目中的函数转化为另一种常见形式。 在学生将函数转化为y=-x2+4x-2=-(x-2) 2+2 后, 教 师便可以进一步要求学生根据函数方程式的特征,对函数的图像进行简单的分析。学生在教师的提醒下可 以得到相应的信息,如函数对称轴方程式为 x=2.顶点 坐标为(2.2),且函数图像开口向下。之后,教师便 可以引导学生将基本信息与题目要求相结合。学生根 据题目所给出的区间判断顶点横坐标与区间之间的位 置,并得到题目中函数的顶点横坐标位于给定的区间 范围之内。当明确顶点横坐标与给定区间范围之间的 位置关系之后,教师便可以进一步引导学生根据之前 所获得的函数图像信息,绘制出简单的函数图像,并 结合题目要求得到题目答案。学生作图如下:
如图 1 所示, 函数的最大值为f(2) =2. 最小值为 f(0) =-2.
在讲解完例题之后,教师便可延伸题目,应用分 类讨论思想, 帮助学生学习更多不同题目的解题方法。 仍以这道题为例, 教师可以更换题目中的区间范围, 并 延伸出顶点横坐标不位于区间范围之内的另一种情 况。结合以上解题过程以及解题过程中所绘出的图像,学生能够在较快时间内掌握相应的解题方法,并得到 答案。
(二)轴定区间动
“轴定区间动”是指在已知二次函数的情况下, 根 据所给出的定义域区间,计算二次函数在区间上的最 值,题目中所给出的定义域区间随参数变化。
例 2:求函数f(x )=x2-2x+3 在 x ∈ [a ,a+2] 上 的最大值和最小值。
与“轴定区间定”问题的解题思路相同,首先教 师可引导学生将函数方程式进行格式上的转化,并根 据所转化出的方程得到函数图像的基本信息。学生在 完成函数方程式的转化之后,可知这一函数图像开口 向上,其对称轴为 x=1.之后教师便可引导学生根据所 给区间进行分类分析。教师可引导学生将定区间中的 a 值与对称轴x=1 联系, 并延伸出不同的分类讨论内容。
首先,学生分析当 x=a 时, a 距离对称轴 x=1 最 近,a+2 距离对称轴x=1 最远。因此, 当x=a 时,ymin=-a2 +3.ymax=a2+2a+3.
其次, 学生便可进行分类分析:①当 0
最后,教师可以组织学生根据二次函数区间图像 进行总结:
当 a<0 时,
(三)轴动区间定
“轴动区间定”这一情况是指,在已知二次函数 的情况下,根据所给出的定义域区间,计算二次函数 在区间上的最值。定义域区间为题目给定区间不变, 但 二次函数图像随参数变化而变化。
例 3:求函数f(x )=x2-2ax+3 在 x ∈ [0.4] 上的 最值。
首先,教师可引导学生将函数方程式进行格式上 的转化,并根据所转化出的方程得到函数图像的基本 信息。其次,学生在完成函数方程式的转化后,可知 这一函数的图像开口向上,其对称轴为 x=a 。最后教师 便可依据分类讨论流程,组织学生根据题目要求和所 给信息进行分类讨论:①当 a<0 时, 0 距对称轴 x=a 最 近,4 距对称轴 x=a 最远。因此,x=0 时, ymin=3.x=4 时, ymax= 19-8a。②当 0 ≤ a<2 时, a 距对称轴 x=a 最 近, 4 距对称轴x=a 最远。因此, x=a 时,ymin=3-a2.x=4 时, ymax= 19-8a。③当 2 ≤ a<4 时, a 距对称轴 x=a 最 近, 0 距对称轴x=a 最远。因此, x=a 时,ymin=3-a2.x=0 时, ymax=3.④当 4 ≤ a 时,4 距对称轴 x=a 最近,0 距对称 轴 x=a 最远。 因 此,x=4 时, ymin= 19-8a,x=0 时, ymax=3.
通过讲解这三种正向型函数的题目,学生能够简 单了解分类讨论思想在数学解题过程中的应用,有意 识地将分类讨论的方法应用于自己的实际解题过程中。 二、“二次函数y=ax2(a ≠ 0)的图像与性质”案例研究
(一)课程分析
1. 教学内容分析
本课内容要求学生能够应用描点法画出二次函数
y=ax2(a ≠ 0)的图像,并能够根据图像认识和理解二 次函数的相关特征。在课堂教学过程之中,教师应培 养学生的探究能力,引导学生探索二次函数 y=ax2 的 图像和图像特征,并引导学生体会分类讨论的思想和 方法。
2. 学生需求分析
学生通过学习本课内容能够掌握二次函数y=ax2 基 本的图像与性质。除此之外,通过课堂学习过程中体 会分类讨论思想,学生能够在数学学习方面获得更加 多样的学习方法,同时也能够在合作和分工的过程中 体会到合作的重要性,综合发展自身的素质和能力。
3. 教学工具需求分析
在教学过程中,教师需要借助多媒体向学生展示 二次函数y=ax2(a ≠ 0) 的图像,同时也需要在黑板 或多媒体显示屏上向学生示范二次函数y=ax2 图像的绘 画过程,并借助图像对二次函数的性质展开讲解。
(二)实际教学流程
1. 环节一:描点绘图
首先,教师可通过提问的方式,引导学生复习之 前的内容,并引入本堂课教学知识:“我们在之前学 习了二次函数这一概念,那么二次函数的定义是什么 呢?今天的学习内容是二次函数的图像,我们在之前 学习过一次函数的图像,那么一次函数的图像是什么 形状呢?我们又是怎样绘制出一次函数的图像呢?教 师”通过这样的复习提问引入,能够使学生在课堂上 提出描点绘图。
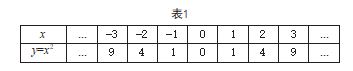
(1)列表:设定 x 取值并计算y 值,列出函数的 对应值表(见表 1)。
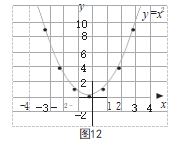
(2)描点:根据所列出的函数取值与对应值,在 平面直角坐标系中画出点的位置。(点位如图 12 所示)
(3)连线:连接各点,并保证曲线光滑,得到函 数y=x2 的图像。
在班级内所有学生完成二次函数y=x2 的图像之 后,教师便可以将学生分为若干个小组,并要求学生 依据相同的方法绘制y=2x2、y=-2x2 与y=-x2 的函数图像。
2. 环节二:归纳共性
教师可提问学生:“刚刚大家依照描点绘图的方法 绘制出了二次函数的图像,请大家以小组为单位,将 这 4 个函数图像汇总在一起并讨论归纳这些函数图像 的共性。”学生在讨论过程中加以总结归纳:“这 4 个 函数图像的对称轴都是y 轴,函数顶点位于原点,函 数图像的开口方向与 x 前的数字正负值有关。”
3. 环节三:探究本质
教师可以将这四个函数图像展示在黑板或多媒体 显示设备上, 并引导学生共同归纳y=ax2 的图像与性质。
4. 环节四:例题解析
(1)写一个顶点在原点,开口向上的二次函数关 系式。(2)画出图像并回答问题:抛物线 y=2x2 顶点坐 标是什么?对称轴是什么?当x= ?时, 函数值最小, 函 数最小值是多少?抛物线 y=2x2 (顶点除外)在 x 轴的 上方还是下方?(3)请你在不画出图像的前提下写出 y=-3x2 和y=3x2 的顶点坐标、对称轴以及函数图像的开 口方向。
5. 环节五:课堂总结
教师:“这堂课上, 我们对二次函数y=ax2(a ≠ 0) 中的 a 的值进行分类, 并展开了关于对应图像的讨论。 通过这一分类讨论过程,我们总结出 y=ax2 的顶点是原 点,坐标轴是y 轴,开口方向与 a 的值之间的关系。” 三、结束语分类讨论思想是现代初中数学教学中常用的教学 思想,能够有效锻炼学生的数学思维和数学能力。这 一教学思想能够进一步深化学生对分类讨论思想的理 解和应用,并帮助学生在之后的学习过程中善于应用 数学思想和数学方法。
参考文献
[1] 朱军平.探析分类讨论法在初中数学解题教学中的 实践[J].数理天地(初中版),2022(6):23-24.
[2] 刘玉芳.分类讨论法在初中数学教学中的渗透研 究[J].试题与研究,2020(21):165.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/69445.html