SCI论文(www.lunwensci.com)
摘 要 : 物理习题课是物理众多课型中至关重要的一种,习题课中的“立———破”思维,先立后 破,破后再破.定位准确,合理立破,层层递进,让不同层次的学生都有收获.
物理习题课是物理众多课型中至关重要的一 种,他直接影响到学生对所学知识的掌握程度,从而 影响学生学习物理的兴趣,兴趣对学生学习物理至 关重要,今天和大家交流我自己认为比较有兴趣且 实用的一种习题课中的“立——— 破”思维.我的这种 思维最早起源于下面这道题.
例 1 现有一个金和银组成的王冠,用排水法 测出其体积为 56.9cm3.若与王冠质量相同的纯金 块和纯银块的体积分别为 52.5cm3 和 96.5cm3 ,则王 冠中银的质量和金的质量之比为多少?
该题中如果将质量相同的金全部换成银质量增 大 44cm3 ,而本题中最后的合金 比纯金体积大 4. 4cm3 ,所以我们可以将纯金和纯银都按质量等分 10 等份,用一份纯银去替换等质量的一份纯金,体积便 会增大 4.4cm3 ,也就是说这道题只用一份纯银去替 换等质量的一份纯金,即合金中有一份纯银,九份纯 金,质量比为 1 ∶ 9.对于密度计算,我们会特别关注 密度定义质量与体积之比即单位体积的质量.但是 上面这道题如果要想到上面的巧解,需要反其道而 行之,想到单位质量的体积,上题中等分完每一份纯 金和纯银的质量都相等,只是体积不同.这道题给了 我启发,让我研究并实践了一种提高物理习题课的 方法——— “立——— 破”思维,在实际教学中取得很好的效果,所谓“立——— 破”就是对物理知识先给学生确 立一个必须达到的物理达标体系即“立”的过程 ,然后 在“立”的基础上要从不同角度,不同层次对这块达标 体系进行拓展拔高,即“破”的过程,与传统的拔高的区 别在于,这种拔高要有巧劲,要在你的“破”的过程中学 生能醍醐灌顶,恍然大悟.这种拔高要有特色,要在你 的“破”的过程中学生能感觉到与众不同,回味无穷.下 面就以一些具体例子来浅谈“立——— 破”思维.
1 机械效率习题课的“立——— 破”思维
例 2 一花瓶质量约为 250kg.为了便于搬运, 工作人员先用质量约为 50kg 的包装箱对花瓶进行 包装 ; 然后用两根粗钢管在高 1.2m 的车厢与地面 之间搭成一个长度约为 4.8m 的简易斜面.装车时, 工作人员要用 1000N 沿平行于钢管方向的推力把 包装好的花瓶匀速推上车.求: ( 1) 对花瓶做的有用 功? ( 2) 搬运花瓶的机械效率? ( 3) 克服摩擦做的 额外功?
对于这道题,学生往往对第一问就出问题了,为 什么会出现这个问题呢? 问题出在“立——— 破”上. 先说说“立 ” ,机械效率中基本的达标线,学生对用 斜面拉高物体,有用功等于重力乘以物体移动的高 度,总功是人用的力乘以沿这个力方向移动的距离,额外功等于总功与有用功之差.学生在“立”的过程 中往往对定义理解不到位,比如用机械拉高物体时 对重力的理解,许多同学理解不到位,会将题目背景 中的所有重力全部代入,这是有问题的 ; 现在说说 “破” ,何为有用功,其实就是你使用斜面的目的,这 是需要学生理解的,不能死记公式,例如上题中克服 包装纸重力做的功是不是有用功,学生自己要思考 这个问题,如果认为是,那就留下花瓶拿走包装纸, 学生肯定不同意,所以包装纸并不是目的,花瓶才 是,包装纸只是为了保护花瓶是不得不做的功,即额 外功.所以对拉高物体的有用功中的重力的理解是 需要打破之前的“立”而“破”出新意,于此类似的便 是经典的在井中捞水桶问题,如果目的是捞水桶,那 克服水桶重力所做的功便是有用功,克服水桶中的 水的重力所做的功便是额外功.如果换个情景,目的 是用水桶打水,那克服水桶重力所做的功便是额外 功,克服水桶中的水的重力所做的功便是有用功.
例 3 利用动滑轮提升一个重为 G 的物块,不 计绳重和摩擦,其机械效率为 60%.要使此动滑轮 的机械效率达到 90% ,则需要提升重力为 G 的物块 的个数为几个?
对于这道题,“立”要求学生必须掌握机械效率 是有用功占总功的百分比.但对于这道题我们可以 这样“破 ” ——— 额外功占总功的百分 比,即逆 向思 维,该题中第一次效率为 60% ,那逆向思维,额外功 占总功的比值为 40% ,就很容易的发现第一次物重 和动滑轮为 3:2.同样第二次效率为 90% ,那逆向思 维,额外功占总功的比值为 10% ,第二次物重和动 滑轮为为 9: 1.由于该题中是用同一个滑轮组将不 同物体提升相同高度,又不计绳重和摩擦,所以额外 功全部来自克服动滑轮自重而产生的功,两次大小 是一样的,所以我们可以将第二次物重和动滑轮为 9: 1 变为 18:2.这样就会发现额外功相同时,第二次 提起的物体重力与第一次提起的物体重力之比为 18:6.为 3: 1.直接得到 3 块的答案.学生需要打破 有用功占总功的百分比,而想到额外功占总功的百 分比,“破”出思维火花. 对于学习能力强的学生我 们需要在已突破的体系下再突破,例如下面这道题.
例 4 某建筑工地上,起重机的吊臂部分为滑 轮组,现用该起重机将质量相同的水泥板吊往高处. 若第一次、第二次、第三次分别将一块、两块、三块水 泥板吊往某高处,三次起重机做的额外功分别为 3000J、4000J、5000J,机械效率分别为 η1 、η2 、η3 ,则 下列关系式正确的是( ) .
A. η 1 >η2 >η3 B.2 η2 >η1 + η3
C.2 η2 = η 1 + η3 D.2 η2 ﹤ η 1 + η3
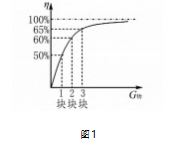
这道题可以尝试让学生在前面已有的突破基础 上,再突破到数学思维巧解这个层面上,如图 1 是物 体重力和滑轮组机械效率的关系图像,我们只要在 这副图像的基础上合理代值,例如提一块水泥板带 机械效率为 50% ,有图像可知,用滑轮组提高物体, 所提物体越重,机械效率越大,则提二块水泥板带机 械效率可以赋值为 60% ,按照图像走势,我们会发 现虽然物体越重,机械效率越高,但是由于机械效率 不能达到 100% ,所以随着物体重力的增加,机械效 率的增大的幅度会渐渐减小,即 η3 - η2 < η2 - η1 , 所以提三块水泥板带机械效率赋值必须小于 70% , 可以赋值为 65% ,将三个机械效率建立联系可以轻 松得到答案 B.我们要根据自己学生的实际情况去 判断孩是止步于“立” ,还是可以“破一”或者是“破 二” ,需要找到最适合自己学生的习题课方案,适合 的才是最美的,才可以培养和保护学生的学习兴趣.
2 压强习题课的“立——— 破”思维
例 5 一质量为 2 kg、厚度均匀的圆柱形容器, 放在水平桌面上,与桌面的接触面积为 0.01m2.现 往容器内注入 0.2 m 深的酒精,此时桌面受到的压 强为 3.2 × 103 Pa ( ρ 酒精 = 0.8 × 103 kg / m3 ) .求 : ( 1) 桌面受到的压力; (2) 酒精对容器底部的压强 ; (3) 酒精对容器底部的压力.
对于压强计算,先说说“立 ” ,学生必须掌握固体压强一般 F = G,P = F/S.液体压强一般 P = ρgh, F = PS.如何“破” ,学生对这几个公式要正确理解, 它们其实没有必须用于固体或液体,四个式子中 P = F/S 和 F = PS 是压强的通用计算公式,固液体都 可以用,没有条件限制,而公式 F = G 是可以用在液 体中的,公式 P = ρgh 也可以用到固体中,只不过有 适用条件--规则柱状均匀物体.上题中如果学生 不能打破这层壁垒,只是按部就班的代公式,由于容 器厚度内外面积的不同,最终造成错误,这道题固体 最终用了 F = PS,而液体却用了 F = G.所以我们必 须帮助打破对于压强计算公式的思维定式,我们要 给学生打破壁垒,帮助学生灵活运用公式.
例 6 一密度为 ρ 的钢制轴承,由粗细不同的 两部分圆柱体构成,粗细圆柱体的高度均为 h.如图 2 甲所示放置时,轴承对水平面的压强为 1.2ρgh,如 图 2 乙所示放置时,轴承对水平面的压强为多少.
这道题目中对桌面的压强,两种放法物体整体 都不是规则柱状均匀固体,原则上是不能用 P = ρgh 求固体压强.适用条件不满足,如何创造条件运用 P = ρgh 求固体压强,如果我们通过挤压上面的物体 的方法可以将物体变为规则柱状均匀固体,也可以 通过挤压下面的物体的方法可以将物体变为规则柱 状均匀固体,两种挤压方法都可以将上下不是柱状 的固体变为上下柱状的固体,那应该采用哪种方法 呢? 我们回到压强的通用公式 P = F/S,不管如何挤 压也不能和这个通用公式相矛盾,也就是说你要保 证所求的压强处的接触面积和压力在挤压过程中不 能出现变化,按照这个想法,我们会发现上面两种挤 压方法都不会改变压力,但是通过挤压下面的物体 的方法可以将物体变为规则柱状均匀固体的方法会 改变物体与桌面的接触面积,而通过挤压上面的物 体的方法可以将物体变为规则柱状均匀固体不会改 变物体与桌面的接触面积.所以应该挤压上面,挤压 之后就可以运用公式 P = ρgh,由于物体密度为定值,而 P = 1.2ρgh,所以挤压之后总高度为 1.2h,下 面粗的圆柱体高为 h,所以高度为 h 的细的圆柱体 由细变粗后高度变为 0.2h,在体积不变的前提下, 细圆柱体高度减小了 5 倍,底面积应该扩大 5 倍,便 可以快速找到粗的底面积是细的底面积的 5 倍,对 于图 2 乙,同样在保证与桌面的接触面积不变的前 提下,也可以通过挤压上面的物体的方法可以将物 体变为规则柱状均匀固体,即把上面的粗圆柱体挤 压成与下面细圆柱体一样粗的圆柱体,粗圆柱体底 面积缩小 5 倍,高度就应该增加 5 倍,变为 5h,在加 上下面细圆柱体的高度 h,总共 6h,从而运用公式 P = ρgh,快速得到如图 2 乙所示放置时,轴承对水平 面的压强为 6ρgh,运用这种挤压变形最重要是要保 证所求压强处的接触面积要保持不变,利用挤压将 不是规则柱状均匀的固体变为规则柱状均匀固体, 从而利用 P = ρgh 快速解出题目,获得成就感,我们 老师要根据自己、学生、学校的实际情况,是让学习 有困难的学生掌握固体压强一般 F = G,P = F/S.液 体压强一般 P = ρgh,F = PS.一般学生要突破到公 式的灵活运用,再有能力的孩子让他创造条件用公 式.让不同层次的孩子都有所获,有所感,收获成功 和喜悦.习题课中的“立——— 破”思维则是在习题课 中的分层教学,教师课前的工作会更多,即要合适高效 的分层,更要针对自己的学生有特色的设计习题课.

我们要研究习题课的设计,这是对学生学习物 理的负责,也是对学生未来的负责.我们要通过习题 课巩固加强学生学习物理的兴趣,不能让习题课只 是机械加强巩固学生的基础知识与基础技能,而应 该是定位准确,合理立破,层层递进,让不同层次的 学生都有收获,都有发展,都能收获幸福感,从而提 高学生学习物理的兴趣.这样一来,习题课会变成学 生学得开心,老师教得顺心的欢乐海洋.
参考文献 :
[1]候利民.例析“数形结合”法在初中物理解题中 的应用[J].数理化学习,2021 (11) : 3-4 .
[2] 肖艳艳.例谈数学思想在初中物理学习中的渗 透[J].湖南中学物理,2019(08) : 31-32 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/68874.html