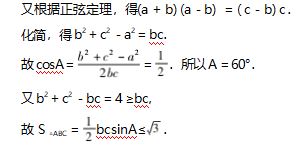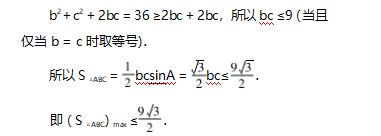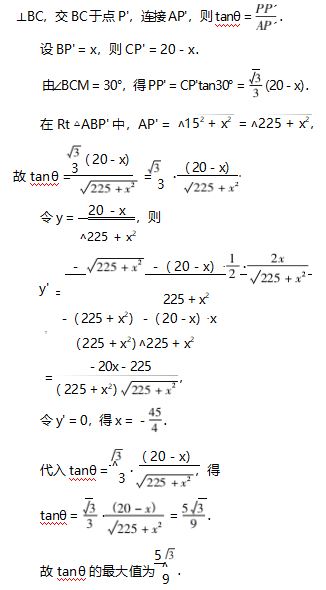SCI论文(www.lunwensci.com)
摘 要 : 解三角形问题在高中数学中占有重要的地位,其中三角形的最值问题由于条件少、难 度大、思维能力较高往往使得学生束手无策,求解这类问题要立足于题设中的关联条件,应用正余 弦定理以及与之相关的面积公式、射影定理等进行求解.
众所周知,解三角形问题一直以来都是高考的重要考点以及热点.常见的解三角形是要给出三角形中的三个条件(必须至少有一边) 才能求解,而只 给出一边及对角、一角、一边及边上中线、一边及所 对角的角平分线等三角形的最值问题也受到了各地 高考的热爱,本文以历年的高考题为例,立足于关联 条件,来破解三角形最值问题.
1 一边与对角
所以 AB + 2BC 的最大值为 2 ^7.
评注 本道题是利用正弦定理以及辅助角公 式,不仅可以求出最大值,还可以求出取值范围,并 且系数可以进行变化,可以加强辅助角公式的训练以及给角求范围的求解.
例 2 ( 2014 年新课标 Ⅰ 卷) 已知 a,b,c 分别为 △ABC 的三个内角 A,B,C 的对边,a = 2.且 ( 2 + b)· ( sinA -sinB) = ( c -b) sinC,则 △ABC 面积的最大值为 .
解析 由 a = 2.且(2 + b) ( sinA -sinB) = ( c- b) sinC,故( a + b) ( sinA-sinB) = ( c-b) sinC.又根据正弦定理,得(a + b) (a-b) = ( c-b) c. 化简,得 b2 + c2 -a2 = bc.
评注 本题的难点是将 2 用 a 代换,这样题中 的等式就是角和边的关系,使用正弦定理把角转化成边,再利用余弦定理求出角,最后用不等式解出面积的最大值.
评注 本题只是求三角形面积的最大值,如果 求面积的取值范围,就不能采用余弦定理,需用正弦 定理,并且需要确定角的范围进而确定面积的取值 范围,对学生掌握辅助角公式以及给角求值等有很 大帮助.
2 只有一角
例 4 ( 2016 年北京理 15) 在△ABC 中,a2 + c2= b2 + ^2ac.
评注 本题是由三边关系来确定一角的大小, 进而求另两角的余弦和的取值问题,主要是辅助角公式的应用以及角的互换和范围确定.
例 5 ( 2015 年湖南) 设△ABC 的内角 A,B,C 的对边分别为 a,b,c,a = btanA,且 B 为钝角.
评注 本题是由边角关系确定三个角之间的关 系以及两角正弦和的范围问题,主要是辅助角公式 的应用以及角的互换和范围确定.
3 一角与其对边上三等分线
评注 本题是由一角与其对边上三等分线来求 面积的最值问题,主要是应用余弦定理以及不等式 进行求解,但其中应用了互补的两角余弦值的和为 零来确定三边关系.
4 一边与其上中线
评注 此题解法较多,除上述解法还可以用切割法、建系、阿氏圆等方法.
5.一角与角平分线
评注 本题主要是应用角平分线将三角形的面积进行分割,然后利用不等式进行讲解.
6 三边关系或三角关系
评注 本题是已知三个角之间的关系,求其中 一个角的取值范围,主要是利用正弦定理进行边角互换,再利用余弦定理以及不等式进行求解.
评注 本题是已知三个角之间的关系,求其中一个角的取值范围,主要是利用正弦定理进行边角互换,再利用余弦定理以及不等死进行求解.
7 综合应用
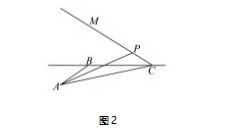
例 11 ( 2015 年 新 课 标 Ⅰ 卷) 在 平 面 四 边 形 ABCD 中,∠A = ∠B = ∠C = 75°,BC = 2.则 AB 的取值范围是 .
解析 如图 1 作△PBC,使∠B = ∠C = 75°,BC= 2.作出直线 AD 分别交线段 PB,PC 于 A,D 两点 ( 不与端点重合),且使 ∠BAD = 75°,则四边形 AB- CD 就是符合题意的四边形,过点 C 作 AD 的平行线交 PB 于点 Q,在△PBC 中,可求得 BP = ^6+ ^2.在△QBC 中,可求得 BQ =-,所以 AB 的取值范围为(^6-^2.^6+ ^2).
评注 此题虽然是已知四边形中的三个角和一 边求其中另一条边的取值范围,但其本质是考查解三角形问题,其实只用到了正弦定理.
例 12 ( 2014 年浙江理 17) 如图 2.某人在垂 直于水平地面 ABC 的墙面前的点 A 处进行射击训 练. 已知点 A 到墙面的距离为 AB,某目标点 P 沿墙 面的射击线 CM 移动,此人为了准确瞄准目标点 P, 需计算由点 A 观察点 P 的仰角 θ 的大小.若 AB = 15m,AC = 25m, ∠BCM = 30°,则 tanθ 的 最 大 值
评注 本题是空间中的解三角形问题,但是本 题中的三角形载体都是直角三角形.
在高考的复习中,应在抓住核心考点的基础下,注 重通性通法的讲解,因此例题的选择很重要,它可以让 学生自己体会更为一般的解题策略,也可以对一般的 解题策略如何应用到具体问题以及如何应用辅助方法 提供“示范”作用,为学生的高效解题提供有力的参考.
参考文献 :
[1] 邹生书.一道三角形面积最大值问题解法赏析 [J].中学数学教学,2019 (03) : 28-29.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/66703.html