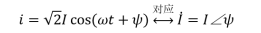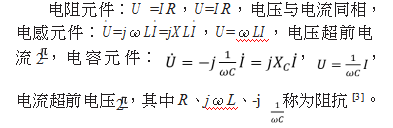SCI论文(www.lunwensci.com):
摘要:正弦稳态电路分析是电路课程的重点内容,是分析互感电路、三相电路、非正弦周期交流电路的基础。正弦稳态电路分析过程借助复数这一数学工具,采用相量法进行分析,分析总体思路是先将正弦量对应成相量,画出电路图的等效相量模型,再根据相量形式对电路进行分析、计算,最后转化为时域下的结果。正弦稳态电路往往采用相量法进行分析,知识点比较零碎,变量之间的关系不仅涉及大小关系,而且还有相位关系。本文借助描述阻抗特性、变量关系、功率问题的三个几何图形和一个角对正弦稳态分析中的知识点进行整合优化,使抽象知识具体化,使零散知识模块化,使理论概念生动化,有助于学生对正弦稳态分析知识的理解和掌握,从而提高学生归纳分析能力,使学习效果事半功倍。
关键词:正弦稳态;三角形;整合优化
本文引用格式:胡亚维.借助于几何三角形对正弦稳态电路分析知识的整合优化[J].教育现代化,2020,7(42):130-133.
Integration and Optimization of Sinusoidal Steady-State Circuit Analysis Knowledge with the Aid of Geometric Triangle
HU Ya-wei,WU Jing
(Xi'an Peihua College,Xi'an,Shaanxi)
Abstract:Sinusoidal steady-state circuit analysis is the key content of circuit course,which is the basis of analyzing mutual inductance circuit,three-phase circuit and non sinusoidal periodic AC circuit.In the process of sinusoidal steady-state circuit analysis,the method of phasor is used with the help of the mathematical tool of complex number.The general idea of analysis is to first correspond the sinusoidal quantity to the phasor,draw the equivalent phasor model of the circuit diagram,then analyze and calculate the circuit according to the phasor form,and finally convert it to the result in time domain.Sine steady-state circuits are often analyzed by phasor method.Knowledge points are fragmentary.The relationship between variables involves not only the relationship of size,but also the relationship of phase.In this paper,the knowledge points in Sinusoidal steady-state analysis are integrated and optimized by three geometric figures and an angle which describe the impedance characteristic,the relation of variables and the power problem,so as to concretize the abstract knowledge and modularize the scattered knowledge,it is helpful for students to understand and master the knowledge of Sinusoidal steady state analysis'so as to improve the students'ability of induction and analysis and make the learning effect more effective with less effort.
Key words:sinusoidal steady state;triangle;integration optimization
电路分析往往是分析两大问题:一是元件/网络特性,此处对应概念为阻抗特性,二是电路拓扑结构之间的约束;分析中涉及三大变量为:电压、电流和功率。本文将正弦稳态电路中的知识点概括成三个几何直角三角形和一个角,分别是描述网络特性的阻抗直角三角形、描述电路拓扑结构对变量约束的电压直角三角形、描述交流功率问题的功率直角三角形和将这三个直角三角形中电路参数、电压变量、电流变量、功率变量问题衔接起来的一个共同角。
一 相量法基础知识
(一)正弦量的相量表示
在线性电路中,如果激励是正弦量,则电路中各支路的电压和电流的稳态响应将是同频率正弦量,若同一电路中正弦量的频率相同,将正弦量可以用一个复常数对应起来,这个复常数定义为正弦量的相量,对应关系见下式。
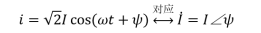
由此可见,在相量形式中确定一个正弦量只需求振幅和初相位[2]。除了正弦量的相量形式以外,还有两大定律的相量形式。
(二)两大定律相量形式
基尔霍夫定律的在相量形式中满足。欧姆定律在相量形式中的满足形式对于不同的元件参数表示有所不同,电压电流关系不仅要分析大小/有效值关系,而且要分析相位关系,同时借助相量图进行几何分析。
单一参数元件电压电流相量形式如下:
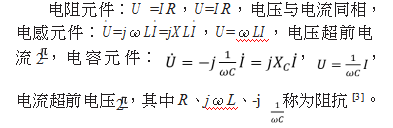
阻抗是相量法分析正弦稳态电路中得出的描述电路特性的一个重要概念,相当于直流电阻电路中的电阻参数,阻抗是一个复数形式,理解正弦交流电路中的阻抗概念能更好的帮助学生理解电路性质、变量关系,下面通过 RLC 串联电路推导说明。
(三)阻抗直角三角形
RLC串联电路的相量形式如图1所示,根据在相量形式中推导出的单一元件电压电流关系,可得出网络的伏安特性如下:
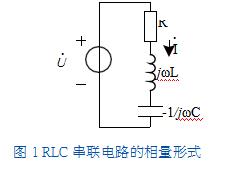

由此可得出,电路中的电阻R、电抗X和阻抗的模之间的关系满足直角三角形的三条边,阻抗角为直角三角形中的一个锐角,将这种关系描述为阻抗直角三角形,如图2所示。直角阻抗三角形不仅对RLC串联电路适用,而且也适用于任何一个正弦稳态电路分析,阻抗Z实部参数R与电路中电阻元件有关,虚部参数X与电路中电感、电容元件有关。阻抗三角形不但反映了交流参数与电阻和电抗性元件的关系,而且也决定了电路中的变量关系和功率问题。
二 电压直角三角形
在对电路网络进行分析过程中,电压、电流关系分析是最基本的分析,根据RLC串联的拓扑结构约束,电压变量之间满足基尔霍夫电压定律,得出:

三角形的三条边,其中φ为总电压与总电流的相位差,根据相量图可以看出φ即为阻抗角。若不考虑相位关系,只考虑大小关系时U、UR、UX之间满足,同样满足直角三角形的三条边。图3中虚线所标示为电压直角三角形,反映了电路中的所有变量相对于结构之间的约束关系。
 三 功率直角三角形
三 功率直角三角形
正弦稳态电路的功率问题相比直流电路做出了单独的说明,因为信号的正弦周期变化使得功率问题分析起来相对比较复杂,与功率有关的概念包括瞬时功率、平均(有功)功率和无功功率、视在功率、复功率等[4]。

其中有功功率P与电阻中的电阻R有关,是电阻元件消耗的功率;无功功率Q与电容、电感元件有关,可正可负,是电路中的电感、电容元件与电源之间进行能量交换的规模;视在功率表示电源设备的容量。通过以上可以看出有功功率P、无功功率Q、视在功率S之间满足直角三角形的三条边,电路中电阻元件消耗功率P与电源容量S之间的关系为cosφ= ,称之为功率因数,因此φ又称为功率因数角。关于功率关系可以得出功率三角形,如图4所示。这个规律也适用于一般情况电路,该三角形能够帮助学生们理解正弦交流电路中各个功率之间的关系。
四 φ角
(一)角衔接作用
阻抗特性分析、电路变量分析得出的三个直角三角形中,都涉及到一个共同的角度—φ角,该角将阻抗特性、电压电流相位关系、功率问题这些知识点系统的衔接了起来,使知识构成了一个整体,三个三角形关系如图5所示。

 (二)φ角讨论
(二)φ角讨论
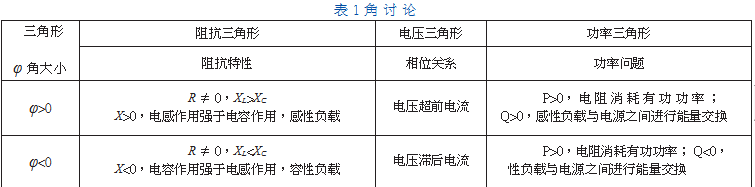
角大小对阻抗特性、电压电流相位关系、功率问题的影响如表1所示。
 五 结论
五 结论
本文通过三个直角三角形对电路中的阻抗特性、电压电流关系和功率问题这些核心知识点和繁多的公式进行了知识整合优化,在实际学习过程中,能帮助学生更好的理解正弦稳态电路部分前后知识衔接关系,能够使知识模块化、具体化,便于学生理解概念,为进一步学习互感知识、三相电路、非正弦周期交流电路部分知识提供必备的知识基础。
参考文献
[1]李瀚荪.电路分析基础[M].4版.北京:高等教育出版社,2011.
[2]高朝,崔乃忠.正弦稳态电路中应用Matlab实现相量法的研究[J].唐山师范学院学报,2016,38(2):53.
[3]邱关源.电路[M].5版.北京:高等教育出版社,2006.
[4]田社平,陈洪亮.关于无功功率的讨论[J].电气电子教学学报,2012,34(1):23.
[5]周悦,霍海波,胡媛,等.动态电路分析法探究,强化融会贯通能力[J].教育现代化,2016,3(23):120-122.
[6]唐甜.《电路分析基础实验》教学改革反思[J].教育现代化,2017,4(19):37-38.
[7]李晓冬,李淑明.电路分析基础实验教材中引入工程应用的探索[J].大众科技,2015,17(09):148-149.
[8]张国光.面向工程教育认证的电路分析基础课程体系建设[J].教育教学论坛,2013(11):152-154.
[9]张立新.正弦稳态电路的分析为何选择复数法[J].哈尔滨师范大学自然科学学报,2015,31(04):73-78.
[10]丁硕,张放,巫庆辉.基于MATLAB/Simulink的正弦稳态电路建模与仿真[J].国外电子测量技术,2015,34(04):68-72.
[11]杨鸿波,高晶敏,魏英,柴海莉.“电路分析”课程研究性教学探讨与案例设计[J].中国电力教育,2014(32):62-64.
[12]张婧婧.基于MATLAB的正弦稳态电路仿真[J].西昌学院学报(自然科学版),2014,28(04):31-33.
[13]路永华.华氏变换及应用[J].陇东学院学报,2014,25(05):19-23.
[14]王文婷,赵锦成,刘金宁,尹志勇.电路分析课程网络化仿真系统设计与开发[J].实验室科学,2014,17(03):83-87.
[15]李慧敏.MuPAD在相量分析法中的应用[J].电脑知识与技术,2014,10(13):3152-3155.
[16]朱莹,贾永兴,陈亮,薛红.电路与信号分析课程内容优化与思考[J].中国教育技术装备,2013(35):66-67.
[17]田慧,闻跃,杜普选.“电路分析”全英文课堂教学探索[J].电气电子教学学报,2013,35(05):37-38+41.
[18]吴涛,张跃辉.Simscape在电路分析教学中的应用[J].实验科学与技术,2013,11(04):313-315.
[19]王翰卓,陈海花.基于Multisim10和Matlab7.0的正弦稳态电路分析[J].电子科技,2013,26(01):146-149.
[20]曹曼,赵锦成.“电路”课程教学改革与实践[J].中国电力教育,2012(21):48-49+53.
[21]腾香.RC电路正弦稳态特性的Multisim仿真分析[J].电子设计工程,2012,20(10):10-12.
[22]拉巴次仁.正弦稳态电路中负载获得最大平均功率情况分析[J].西藏大学学报(自然科学版),2012,27(01):107-110.
[23]王文婷,王勇,刘金宁.电路分析课程教学改革的实施——课堂引入教学演示[J].中国现代教育装备,2012(07):76-78.
[24]何川.电路原理课教学实践探析[J].科技资讯,2012(06):195.
[25]田社平,陈洪亮.关于无功功率的讨论[J].电气电子教学学报,2012,34(01):23-25+42.
[26]徐国峰,宋卫菊,卢松玉,王玫.电路分析课程教学改革与研究[J].科技信息,2011(25):186+185.
[27]徐国峰,宋卫菊,卢松玉,王玫.电路分析课程教学改革与研究[J].科技视界,2011(01):90-91.
[28]贺为婷,肖博潇.正弦稳态电路的MATLAB/simulink仿真分析[J].电子设计工程,2011,19(07):32-34+38.
[29]吴大中.电路分析课程教改之认识[J].信息系统工程,2011(02):107-109.
[30]白凤仙,董维杰,解永平,刘惠.浅谈“电路理论”课程教学中的体会[J].电气电子教学学报,2010,32(06):67-69.
[31]肖志红.电类基础课程教学改革探讨[J].中国现代教育装备,2010(19):68-70.
[32]汤仁彪.PLECS在电路分析中的应用[J].金华职业技术学院学报,2010,10(03):33-37.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/31435.html