SCI论文(www.lunwensci.com)
摘要 : 思维能力培养是义务教育阶段数学教学的重点任务 。教师在课堂教学中应该围绕 数学思维的培养 , 探寻有效的教学策略 。本文结合教学案例 , 从重启发 , 鼓励学生主动 思考 ; 重引导 , 鼓励学生敢于发现 ; 重方法 , 培养学生解题能力三个方面 , 探讨了小学 数学思维能力培养的课堂实践研究 。
关键词 : 思维能力,小学数学,课堂实践
《义务教育 数 学 课 程 标 准(2022年 版) 》明确了培养数学思维的价值和意义 , 将“会用数学思维思 考现实世界”列入了该阶段的学生核心素养中 , 证 明思维能力培养在数学教学中处于重要位置 。对小学生而言 , 数学思维主要指运算能力 、推 理 意 识 、 应用意识等方面 。在数学教学实践中 , 教师应借助数学问题有意识地培养和发展学生推理能力 , 引导 学生通过主 动 探 究 不 断 提 升 问题的分析与解决能 力 , 从而提升数学思维能力 。
一 、重启发 , 鼓励学生主动思考
在数学课堂实践中 , 教师时常发现 , 那些数学 思维表现积极的学生均具有近乎相同的学习特征 。 学习过程中 , 聚精会神 、全情 投 入 ; 遇 到 问 题 时 , 思维逻辑反应普遍较快 , 爱提问题 , 更爱答题 , 尤 其是数学难题 ; 做题时 , 通常不满足某 一 种 方 法 , 而是从多种解法中找出最简算法 ; 对与现实生活关 联的数学题型 , 兴趣十足 , 愿意动脑思考 , 不怕困 难 , 能自主找到解决办法 。 上述学生的 种 种 表 现 , 为教师课堂教学提供了重要依据 , 提醒教师应从思 维启发开始 , 为数学思考创造各种机会或条件 , 通 过具体的数学问题引导 , 鼓励学生在操作观察基础 上展开思考 , 在获取数学知识同时促进思维发展 。
以“圆周率”教学为例 。 圆周率是圆周长与直径 的比值 , 以常量 π 来表示 , 其数值是 一 个无理数 。
为帮助学生深入理解圆周率概念 , 教师针对教学内 容布置了一项测量与计算的作业 , 要求学生课后回 家亲自完成 。作业内容是 : 选取家中 2 到 3 件圆形 物体 , 先分别测量这些物体的直径和周长 , 然后再 算出周长与直径的比值(周长除以直径) 。学生拿到 作业后 , 自主选择物体展开测量与计算 。第二天上 课时 , 学生将自己的测量与计算结果汇报给 教 师 。 多数学生得出的结果与圆周率 π 的数值相当(排除 个别误差) 。在此过程中 , 有个别学生发现自己 的 结果与其他人差别较大 , 向教师提出疑问 : 为什么 我的结果会有这么大的出入? 教师并没有直接给出 答案 , 而是引导学生从“测量”与“计算”两个环节来 检查其中可能存在的问题 。学生经过教师点拨 , 最 终找出了问题所在 : 部分学生在物品选择上出现了 问题 , 选择的是椭圆或类圆形 , 而并 非 标 准 圆 形 ; 还有部分学生在测量环节中出现问题 , 没有找准圆 心 , 造成直径测量数据有误 ; 个别学生在计算环节 出了问题 , 虽然测量数据正确 , 但因粗心大意导致 结果出现较大偏差 。学生在经过实操与计算后 , 真 正掌握了圆周率求法 。课后依然有学生提问 : “是 不是任何一个标准圆形 , 它的周长总是直径大小的 3倍多一点呢?”这个问题引起了大家的关注 , 教师 顺势引导学生进行深入讨论 。讨论之后 , 有学生这 样回答 : “可以通过计算证明 。 当圆的直径是 1 米 时 , 圆周长是 3.14米 ; 当 圆 的 直 径 是 2 米 时 , 圆周 长 是 6.28 米 。 当 直 径 是 3 米 时 , 圆 周 长 是 9.42米 。可见 直 径 增 大 几 倍 , 圆 周 长 也 随 之 增 大 几倍 。两者之间总是 3倍多一点的关系 。无论圆多 大或多小 , 圆周长总是直径的 3倍多一点 。”这样的 教学设计 , 不仅可以增强学生对数学知识的理解记 忆 , 更在动手过程中启发了学生思维 。通过动手操 作与具体运算 , 促进学生数学思维能力的发展 。
二 、重引导 , 鼓励学生敢于发现
思维能力的培养不仅在于教师引导 , 更应鼓励 学生在数学中 进 行 自 我 发 现 , 通 过 问 题 辨 析 和 探 究 , 培养学生开动脑筋 、主动思考的习惯 。这不仅 有助于学生对数学知识的深刻理解 , 更在此过程中 培养了 学 生 严 谨 的 思 维 能 力 , 形 成 重 理 论 、有 条 理 、合乎逻辑的思维品质 。
以“比例”教学为例 。 教学中 , 某些学 生 对“组 成比例的四个数均不为零”这个前提条件产生了疑问 。课堂 上 , 某 位 学 生 以 实 例 提 出 自 己 的 不 同 观点 : “拿 0 ∶ 2=0 ∶ 3 举例 , 前 一 项的比值为 0. 后一项的比值也为 0. 因此该等式成立 , 也符合比例 的定义 , 有 0 的也能组成比例 。”与他持有相同观点 的学生补 充 道 : “比 例 是 除 法 的 变 形 , 0 是 不 能 当 作除数 , 但可以作为除数使用 , 所以我认同刚才这 位同学说 法 。”他 们 的 疑 问 建 立 在 对“比 例”“比 值” “比例与除法”“比与分数”等数学知识有一定认知基 础之上 。此时 , 教师不应“唯书本论”, 应鼓励学生 质疑 , 并从中加以引导 , 在保护学生求 知 欲 同 时 , 体现数学科学严谨的学科特点 。 于是 , 该教师综合 上述同学疑问 , 引导学生关于本话题展开讨论 。 片刻之后 , 有学生便对上述学生的质疑做出了回 应 :“假设 0 ∶ 2=0 ∶ 3 这个比例成立 , 那么根据比例的性质 , 该比例应该有其他 3种不同的比例形式 , 即2 ∶ 0= 3 ∶ 0. 2 ∶ 3=0 ∶ 0. 3 ∶ 2=0 ∶ 0.这三个比例中 , 都有 0作为后项使用 , 与刚才那位同学所说 的除数不能为 0 相互矛盾 。”还有学生补充道 : “将 上述三个比例的前后项分别进行比值计算 , 除了第 1 个 无 法 计 算 外 , 第 2 个 比 例 的 前 项 比 值 为 2/3. 第 3个比例的前项比值是 3/2. 显然与它们后项的比值不同 。”经过深入思考 , 学生终于弄清楚了“组成比例的四个数均不 为 零”结 论 正 确 。 在 课 堂 教 学过程中 , 部分学 生 会 对 课 本 或 教 师 提 出的 数 学 结论 、数学性质概念等提出 自我看法 , 对“权威”发起挑战 。这本身就是一种愿意动脑 、主动思考的积极表现 , 此时 , 教师不应压制 , 反而要予以鼓励 。看似这些突发性问题打断了课堂教学安排 , 但它们的出现实则构成了数学课堂重要的教学资源 。教师应积极引 导 , 启 发 学 生 深 入 思 考 , 鼓 励 学 生 主 动 探究 , 这对培养数学思维 , 发展数学能力具有重要的实践价值 。

三 、重方法 , 培养学生解题能力
思维能力并非 一 种抽象 的 概 念 , 与 知 识 储 备 、技能方法之间存在着直接关联 。数学思维能力不会凭空出现 , 需要在具体的数学情境中 , 借助问题解决能力提升而逐渐生成 。所谓“举 一 反三”“熟能生巧”, 均体现了 方 法 技 巧 对 思 维 形 成 的 重 要 作 用 。因此 , 在小学数学课堂上 , 教师应重视数学方法教学 , 加强对学生在问题解决能力方面的培养 , 促使学生数学思维能力发展 。
1. 用“画线段”方法提升解题能力
以应用类题型教学为例 。小学数学教材中的很多应用题多源于生活 , 是对现实生活中所包含的数学问题进行抽象与概括 。对于小学生而言 , 他们形象思维能力比较突出 , 但抽象思维能力通常 较 弱 。此时 , 若能借助某种具体化工具 , 将应用题型中的抽象内容以形象化方式予以展示 , 即可帮助学生快速理解题意 , 找到问题解决方法 。经过大量数学实践可以发现 : 多数应用类题型均可通过“画线段”方法予以解决 。在教学中 , 教师通过示范 、引导 、模拟 、运用等环节 , 让学生逐渐掌握“画线段”的解题方法 , 有助于提升学生解题能力 , 促进数学思维形成 。 以小学数学教材中常见的行程类应用题 为 例 。题目是 : 甲乙两地相距 545公里 , 汽车从甲地开往乙地 , 行走 3个小时后 , 剩余的路程比已经走过的还多 35公里 , 问汽车的平均速度是 多 少? 题 目 中包含多组关系 , 学生仅凭读题很难进行正确 解 答 。
在利用“画线段”方法的帮助下 , 学生能将题目中的 条件以可视的线段方式呈现 , 更容易厘清题中的条 件关系 , 快速列出本题算式(545-35) ÷ 6. 并最终 得出正确答案 , 即汽车平均速度为 75公里/小时。
2. 用“数形结合”方法拓展解题思路
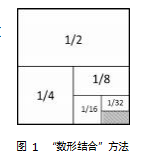
数形结合既是一种解题方法 , 也是一种数学思维 。数形结合打破了小学数学教材中代数、 几何等 知识障碍 , 凭借形象具体的直观体验 , 增强学生对 题目的理解 , 从而增强对某类数学问题的快速解决 能 力。 以 下 题 为 例 : 求 1 - 1/2 - 1/4- 1/8 - 1/16-1/32的 数 值。 常 规 解 法 是 : (1) 逐 步 计 算。 按照运算规则 , 一 步一 步演算 , 最终得出结果。 本 题计算过程为 : 1-1/2-1/4-1/8-1/16- 1/32= 1/2-1/4- 1/8- 1/16- 1/32= 1/4- 1/8- 1/16- 1/32= 1/8- 1/16- 1/32= 1/16- 1/32= 1/32; (2) 减项合并。 将被减数进行组合 , 得出总数 , 最 后统 一 减 去。 即 1 - 1/2- 1/4- 1/8- 1/16- 1/32= 1- (1/2+ 1/4+ 1/8+ 1/16+ 1/32) = 1-31/32= 1/32. 除 了 常 规运算, 本 题 还 可 通 过“数形结合”方法(见图 1)进行计 算 , 这 样 可 以 简 化 运算过 程 , 直 接 得 出 结 果。在“数 形 结 合”解 题 方 法和 思 维 影 响 下 , 学 生 下次遇 到 类 似 具 有 规 律 性的多式运算时 , 例 如 : 求21+23+25+27. 可结合“梯形”图形进行解题思维 转化(见图 2) , 快速解决数学问题 , 提升数学解题 能力。
3. 用“估算”方法提升验算效率
计算能力是小学阶段数学教学的重点 , 是学生 在理解运算法则基础上 , 灵活采用适当法则进行具 体运算能力体现。 为保证运算的正确率 , 运算之后 对运算结果进行验算 , 是其中必不可少的步骤。 常 规验算是将算式重新计算一遍或采用另一种方法进 行计算 , 假若结果一样 , 则可基本判定该算式的运 算过程及结果 是 正 确 的。 但 这 种 方 式 往 往 费 时 费 力 , 占用大量时间 , 不利于学生思维发展。 在教学 过程中 , 可采用“估算”法来简化这个步骤 , 从中提 升学生的解题效率 , 发展学生数学 解 题 能 力。 如 : 圆的直径是 12厘米 , 求圆的面积。 学 生 利 用 圆 的 面 积 公 式 进 行 计 算 S = πr2 = 3.14× ( 12/2) 2 = 3.14× 36= 113.04(厘米2 ) 。 这个结果到底对不 对 呢? 按常规验算 , 学生会重新检查整 个 运 算 过 程 , 费时费力。 倘 若 将 3.14看 作 3. 代 入 算 式 , 通 过 估算 , 可以得出 3× 36= 108. 因为 3<3.14. 所以 估算值应 比 实 际 值 小 , 相 差 的 0.14× 36. 应 该 在 5左右 , 所以 , 基本上可以确认计算结果正确。 这 是比 较 简 单 的 “估 算”验 算 应 用 , 像 9.8 × 12、 10.01× 43等这样的大数运算 , 也可以通过“估算” 方法对结果进行验算 , 提升解题效率。
上面所提到的几种解题方法 , 只是小学阶段众 多解题方法的简单示意。 在小学数学教材中 , 对学 生解题方法的启发与引导内容分布在每个学段及不 同章节之中 , 需要教师对此认真总 结、 详 细 归 纳 , 以便引导学生理解掌握并能熟练应用。 入编教材的 题型案例均具有代表性 , 学生只有熟悉教材中经典 题型各种解法 , 才能在面对新的数学问题时将 日常 解题能力进行 迁 移 , 并 循 环 形 成 新 的 数 学 解 题 能 力 。伴随该过程 , 学生的数学思维则得到进 一 步的 升华与巩固。
参考文献
[1] 刘代娣. 扬 思 维 风 帆 推 数 学 成 长— 谈 小 学 生 数 学 思 维能力的培养策略[J]. 学苑教育 , 2020(31) : 43- 44.
[2] 李保会. 小学数学教学中学生数学思维能力的培养[J]. 数学学习与研究 , 2022(12) : 77- 79.
[3] 王学兵. 小学数学教学中注重学生思维能力的培养[J]. 天津教育 , 2021(30) : 49- 50.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/63986.html