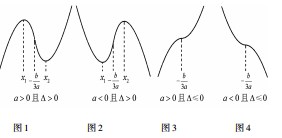
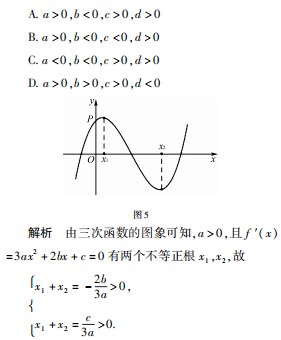
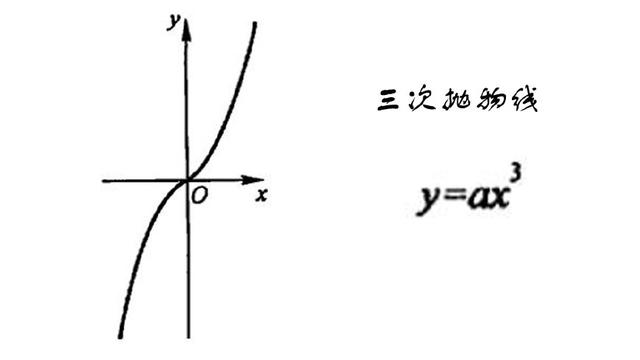
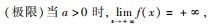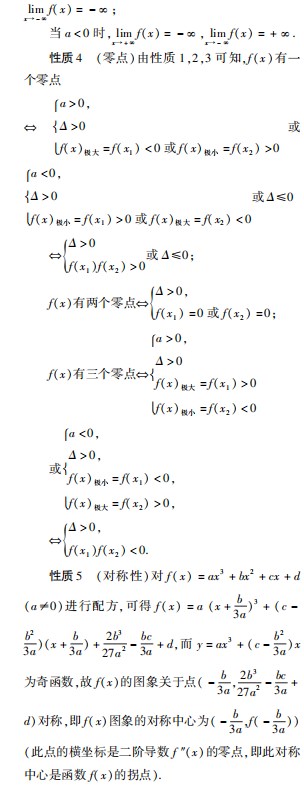例2(2013年高考全国Ⅱ卷·理10文11)已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是().
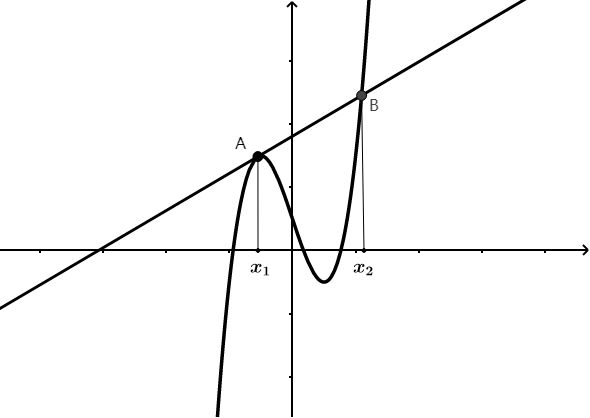
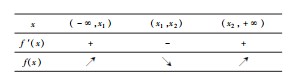
D.若x0是f(x)的极值点,则f′(x0)=0解析显然A,B,D项均正确;对于C项,若x0是f(x)=x3+ax2+bx+c的极小值点,则f(x)的大致图象如图1所示,f(x)在区间(-∞,x0)上先递增后递减,即C项错误.
点评三次函数的单调性分为“增”“减”“增减增”“减增减”四种情形,只需结合其图象即可得出正确的判断.
例3(2021年高考全国乙卷·理10文12)设a≠0,若x=a为函数f(x)=a(x-a)2(x-b)的极大值点,则().
解析令f(x)=0,解得x=a或x=b,即x=a
与x=b是f(x)的两个零点.
(1)当 a > 0 时,由三次函数的性质可知,f( x)的单调性为“增减增”,要使 x = a 是 f( x)的极大值点,则函数 f(x)的大致图象如图 6 所示,故 0 < a <b,从而有 ab > a2;
(2)当 a < 0 时,由三次函数的性质可知,f( x)的单调性为“减增减”,要使 x = a 是 f( x)的极大值点,则函数 f(x)的大致图象如图 7 所示,故 b < a <0,从而也有 ab > a2.
综上,ab > a2,即正确选项为 D.
点评 本题在绘制三次函数的图象时,需要注意 x = a 既是函数 f( x)的极大值点,又是 f( x)的零点,同时 a 的正负情况还决定了函数的单调性.
例 4 (2013 年高考安徽卷·理 10) 若函数f(x) = x3+ ax2+ bx + c 有极值点 x1 ,x2 ,且 f( x1 ) =x1 ,则关于 x 的方程3[f(x)]2+ 2af(x) + b = 0 的不同实根个数是( ).
A. 3 B. 4 C. 5 D. 6
解析 因为 f( x) = x3+ ax 2+ bx + c 有极值点x1 ,x2 ,则方程 f ′(x) = 3x2+ 2ax + b = 0 的两根为 x1 ,x2 ,故方程 3 [f(x)]2+ 2af( x) + b = 0 等价于 f( x)= x1 或 f(x) = x2.
因此,问题转化为判定直线 y = x1 ,y = x2 与曲线 y = f(x)交点的个数.
(1)若 x1 > x2 ,注意到 f( x1 ) = x1 ,故 f( x)的大致图象如图 8 所示,此时直线 y = x1 ,y = x2 与曲线 y= f(x)共有三个交点;
(2)若 x1 < x2 ,f(x)的大致图象如图 9 所示,此时直线 y = x1 ,y = x2 与曲线 y = f(x)共有三个交点.综上,不论 x1 ,x2 的大小关系如何,关于 x 的方程 3 [f(x)]2+ 2af(x) + b = 0 的不同实根个数都是3,故选 A.
点评 本题中三次函数 f(x) = x3+ ax2+ bx + c的单调性为“增减增”,分类讨论的标准在于区分x1 ,x2 中哪个是极大值点、哪个是极小值点.
2. 4 零点问题
例 5 (2015 年高考安徽卷·理 15)设 x3+ ax+ b = 0,其中 a,b 均为实数. 下列条件中,使得该三次方程仅有一个实根的是 (写出所有正确条件的编号).
①a = - 3,b = - 3;②a = - 3,b = 2;③a = - 3,b> 2;④a = 0,b = 2;⑤a = 1,b = 2.
解析 设函数 f(x) = x3+ ax + b,因为仅有一个零点,故其图象有三种可能:
(1)当 f ′( x) = 3x2+ a 的零点的判别式 Δ =- 12a≤0 时,f(x)在 R 上单调递增,恰好一个零点,故④⑤正确;
综上,使得该三次方程仅有一个实根的条件是①③④⑤.
点评 本题主要考查三次函数 y = x3+ ax + b 的零点个数,结合三次函数的图象特征即可轻松破解.例 6 (2012 年高考全国大纲卷·理 10)已知函数 y = x3- 3x + c 的图象与 x 轴恰有两个公共点,则 c 等于( ).
A. - 2 或 2 B. - 9 或 3
C. - 1 或 1 D. - 3 或 1
解析 由 y = x3- 3x + c 得 y′ = 3x2- 3,其导数的零点为 x = ± 1,此即 y = x3- 3x + c 的极值点.因为函数 y = x3- 3x + c 的图象与 x 轴恰有两个公共点,即有两个零点,故 y极大 = y x = - 1 = 2 + c =0 或 y极小 = y x = 1 = - 2 + c = 0,即 c = - 2 或 2.
点评 三次函数恰有两个零点,有两种情形:极大值为零或极小值为零,解题时要注意考虑全面.例 7 (2020 年高考浙江卷·9)已知 a,b∈R且 ab≠0,对于任意 x≥0 均有(x - a)(x - b)(x - 2a- b)≥0,则( ).
A. a < 0 B. a > 0 C. b < 0 D. b > 0
解析 设函数 f(x) = (x - a) ( x - b) ( x - 2a -b),显然其零点为 x = a,x = b 与 x = 2a + b.注意到 ab≠0,故 b≠2a + b. 下面就零点是两个还是三个来展开讨论,并绘制函数图象:
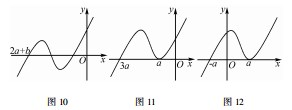
(1)若三个零点两两不相等,则由 x≥0 时恒有f(x)≥0 可知 f(x)的图象如图 10 所示,其三个零点a < 0,b < 0,2a + b < 0;
(2)若 a = b,则 f( x) = (x - a)2( x - 3a),符合题意的图象如图 11 所示,此时 a = b < 0;
(3) 若 a = 2a + b,则 a + b = 0,故有 f ( x) =(x - a)2(x + a),符合题意的图象如图 12 所示,此时 a > 0,b < 0.
综上,b < 0,正确选项为 C.
点评 本题中,当函数 f(x)恰有两个零点时,要注意 x = a 为非变号零点,这对绘制函数图象至关重要.
参考文献:
[1] 陈泽瑛. 三次函数零点个数问题的分类讨论标准[J]. 中学生数学(高中),2017(11):31 - 33.
[2] 苏艺伟. 微专题之三次函数[ J]. 数理化解题研究,2020(22):16 - 19.