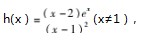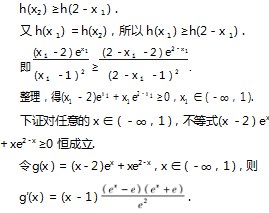SCI论文(www.lunwensci.com):
摘 要 : 函数零点是历年高考命题的重点,也是函数应用的基础,此内容可与多种函数及函数 的图象、性质相结合,从近几年高考来看,零点问题与函数图象交汇在客观题、与导数结合在解答题 中出现,是考查函数与方程、数形结合、转化与化归思想的重要载体.
关键词 :常见函数;零点问题;数形结合;求解策略
1 回归定义,溯本求根
例 1 已 知 定 义 在 R 上 的 函 数 f ( x ) =
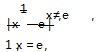 ,若关于 x 的函数 y=f 2 (x ) -mf(x )+m -1(其中 m > 2)有 n 个不同的零点 x 1,x2,x3, …,xn,则f(x 1 +x2 +x3 + …+xn ) = .
,若关于 x 的函数 y=f 2 (x ) -mf(x )+m -1(其中 m > 2)有 n 个不同的零点 x 1,x2,x3, …,xn,则f(x 1 +x2 +x3 + …+xn ) = .
解析 令f 2 (x ) -mf(x ) +m -1 =0,
解得f(x ) =1 或 m -1 .
当 x≠e 时,函数解析式f(x )

若f(x )

=1,解得
x 1 =e -1,x2 =e +1 .
若f(x )

=m -1,解得
当 x =e 时,函数解析式f(x ) =1,即 x5 =e.
综上所述 x 1 +x2 +x3 +x4 +x5 =5 e.
易知f(x 1 +x2 +x3 + …+xn ) =

.
例 2 (2019 年全国Ⅱ卷文)已知函数f(x ) = (x -1)lnx-x -1,证明 :
(1)f(x )存在唯一 的极值点;
(2)f(x ) =0 有且仅有两个实根,且两个实根互为倒数.
证明 (1)函数f (x ) 的定义域为(0,+ ∞ ), 导函数f ′(x ) =lnx -

,此时f ″(x ) =
 +
+  > 0, 所以f ′(x )在(0,+ ∞ )单调递增.
> 0, 所以f ′(x )在(0,+ ∞ )单调递增.
又f ′(1 ) = -1 < 0,f ′(2) =ln2 -

> 0,所以 存在 x0 ∈ (1,2),使得f ′(x0 ) =0.
易知,当 x ∈ (0,x0 )时,f ′(x ) < 0,当 x ∈ ( x0,+ ∞ )时,f ′(x ) >0,即f (x )在(0,x0 )上单调递减, f (x )在(x0,+ ∞ )上单调递增.
所以当 x =x0 时,f (x )有极小值.
所以f(x )存在唯一 的极值点.
(2)由(1)知,f(x )在 x =x0 处取得最小值f(x0 ) = (x0 -1)lnx0 -x0 -1 .
又f ′ ( x0 ) = lnx0 -

=0,即 lnx0 =
 ,所以f(x0 ) =-
,所以f(x0 ) =- -x0,显然f(x0 ) <0.
-x0,显然f(x0 ) <0.
因f(e2 ) =e2 -3 >0,f (x )在(x0,+ ∞ )上单调
递增,所以存在唯一实数 m ∈ (x0,+ ∞ ),使f( m ) = ( m -1)lnm-m -1 =0.
又f (x )在(0,x0 )上单调递减,且
 ∈ (0,x0 ),
∈ (0,x0 ),
所以f(x ) =0 有且仅有两个实根 m,
 ,且两个实根互为倒数.
,且两个实根互为倒数.
评析 求函数零点的常用方法 :一是通过解对 应方程,求实数解;二是通过作函数图象,利用数形 结合求交点横坐标,但需要注意函数的定义域,分段 函数的零点检验.
2 巧用对称,不攻自破
例 3 ( 成都树德中学期末考试) 已知 x 1 是 函数f( x ) =x log2 x -2020 的一个零点,x2 是函数 g( x ) =x ·2 x -2020 的 一 个零点,则 x 1 x2 的值为
解析 令f(x ) =xlog2 x-2020 =0,得
log
2 x =

易知,函数 y =log2 x 与 y =
 图象交点坐标为 A(x 1,y1 ) .
图象交点坐标为 A(x 1,y1 ) .
令 g(x ) =x ·2
x -2020 =0,可得 y =2
x 与 y =
 图象交点坐标为 B(x2,y2 ) .
图象交点坐标为 B(x2,y2 ) .
因函数 y=log2 x 与 y =2x 的图象关于 y =x 对称,所以点 A(x 1,y1 )与 B(x2,y2 )关于 y=x 对称,即
y1 =x2,y2 =x 1 .
又 y1 =

,所以 x 1 x2 =2020.
例 4 (2017 年全国 Ⅲ卷) 已知函数f ( x ) = x2-2x+a(ex-1 +e-x+1 )有唯一零点,则 a =( ).
解析 f(x ) =x2 -2x +a ( ex -1 +e-x +1 ),令 t = x -1,则 g(t ) =f( t +1) =t2 +a (et +e -t ) -1 .
易知 g( -t ) =g(t ),所以函数 g (x )为偶函数. 又函数f(x )有唯一零点,所以函数 g (x )也有唯一零点.
由偶函数图象关于 y 轴对称知,g (0) =2a- 1 -0,解得 a=
 .
.
评析 解决函数零点不可求的客观题时,要有 二个意识 :一是会转化,函数零点、方程的根、两个图 象的交点三者之间等价转化;二是要有整体观,结合 图象的表征深化到图象的对称性 : 中心对称、轴对 称,奇函数或者偶函数的零点关于数轴原点对称,且 所有零点之和等于 0.
3 合理设参,统一变量
例 5 已 知 f ( x ) =
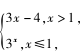
若 a < b,
f( a ) =f( b ),求 a+3b 的取值范围 .
解析 函数 y =f ( x ) 的图象如图 1 所示,令f( a ) =f( b ) =m,a < b,由图知 m ∈ (0,3] .
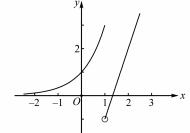 图 1
图 1
因函数 y=log2 x 与 y =2x 的图象关于 y =x 对
又f( a ) =3 a =m,所以 a =log3 m.
由f( b ) =3 b-4 =m,知 3 b =4 +m.
所以 a+3b =log3 m+m+4.
构造函数 g(x ) =log3 x +x +4,x ∈ (0,3],易知g (x )在(0,3]上单调递增.
所以 g (x )的值域为( -∞,8] .
即 a+3b 的取值范围是( -∞,8] .
评析 将方程问题转化为图象的交点问题,数 形结合找到参数的切入点,联立方程组,将多变量问 题转化为单变量问题,方便在化简、求最值时使用均 值不等式、配方、构造函数判断单调性、比较大小等, 但要注意变形过程的等价性.
4 巧用模型,化动为静
|log3 x |,0 <x≤3,
例6 已知函数f(x ) =

若
函数 y=f(x ) -m 有四个不同的零点 x 1,x2,x3,x4,满足 x 1 < x2 < x3 < x4,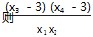 的取值范围是 .
的取值范围是 .
解析 函数 y =f ( x ) 的图象,如图 2 所示,令 f(x 1 ) =f(x2 ) =f( x3 ) =f( x4 ) = m,则 m ∈ (0,1 ),
0 < x 1 < 1,1 < x2 <3 .
图 2
由f(x 1 ) =f(x2 ),知 |log3 x 1 | = |log3 x2 | .
即-log3 x 1 =log3 x2,解得 x 1 x2 =1 .
由f(x3 ) =f(x4 ) =m,知 x2 -10x +24 -3 m=0.
由根与系数的关系,得
x3 +x4 =10,x3 x4 =24 -3 m. ①
(x3 -3) (x4 -3) =x3 x4 -3(x3 +x4 ) +9,
将①式代入上式,得
(x3 -3) (x4 -3) =3 -3 m ∈ (0,3) .
综上所述
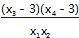 的取值范围是(0,3).
的取值范围是(0,3).
评析 依据题目条件准确画出函数图象,使复 杂的代数问题变得形象直观,结合图象建立等量关 系、不等关系,求得零点的分布.
5 数形结合,相得益彰
例 7 (2020 年全国Ⅲ卷)设函数f(x ) =x3 + bx +c,曲线 y=f (x )在点(
 ,f(
,f( ))处的切线与 y轴垂直.
))处的切线与 y轴垂直.
(1)求 b;
(2)若f (x )有一个绝对值不大于 1 的零点,证 明 :f (x )所有零点的绝对值都不大于 1 .
解析 (1)b =-

过程省略.
(2)f(x ) =x3 -
 x +c,令f (x ) =0, 解得-c=x3 -
x +c,令f (x ) =0, 解得-c=x3 - x.
x.
构造函数 g(x ) =x3 -
 x,
x,
导函数 g′(x ) =3(x2 -

) .
由 g′(x ) >0 知,x <
 -或 x >
-或 x > ;
;
由 g′(x ) <0 知,-
 < x
< x  < .
< .
所以 g(x )在( -∞,-

),(

+ ∞ )单调递
增,g(x )在( -  ,
,  )单调递减.
)单调递减.
图 3
综上所述,当f (x )有一个绝对值不大于 1 的零 点时,f (x )所有零点的绝对值都不大于 1 .
评析 本题考查导数的几何意义、与零点有关 的不等式证明,体现了数学运算、逻辑推理的核心素 养. 运用导数研究函数的零点或者方程的根,是高考 热点问题,以函数的单调性为切入点,画出函数大致 图象,以便确定函数零点的分布、最值情况,真正体 现数形结合的灵活运用.
6 以退为进,海阔天空
例 8 (2020 年浙江卷) 已知 1 < a ≤2,函数 f(x ) =ex -x -a,其中 e =2. 71828 … 是自然对数的 底数;
(1)证明 : 函数 y =f (x )在(0,+ ∞ )上有唯一 零点;
(2)记 x0 为函数 y =f ( x )在(0,+ ∞ )上的零
点,证明  ≤x0 ≤
≤x0 ≤ 
证明 ( 1 ) 由 f( x ) = ex -x -a 知,导 函 数 f ′( x ) =ex -1,显然,函数 y =f ( x ) 在(0,+ ∞ )上单调递增.
又f(0) =1 -a <0,f(2) =e2-2 -a >0,
所以函数 y=f (x )在(0,+ ∞ )上有唯一零点.
(2)下证 ①f(
 ) ≤0.
) ≤0.
故构造函数 g(x ) =ex -x-x2 -1,x ∈ [0,1] .
所以 g′(x ) =ex-2x-1,g″(x ) =ex-2.
令 g″(x ) =0,解得 x =ln2.
易知函 数 g′ ( x ) 在 ( 0,ln2) 上 单 调 递 减,在 (ln2,1)上单调递增.
又 g′(0) =0,g′(1) =e-3 <0,所以,当 x ∈ [0, 1]时,g′(x ) <0,函数 g (x )在[0,1]上单调递减.
所以 g(x ) ≤g(0) =0,即 ex -x -x2 -1 ≤0,由 此可得f(
 ) ≤0.
) ≤0.
下证 ②0≤f(

) .
因为f(

) =e

-

-a =e
 -
- -
- ·2(a -1) -1,
·2(a -1) -1,
构造函数 h (x ) =ex -x -
 x2 -1,x ∈ [0, 2 ], 所以 h ′(x ) =ex -x -1,h ″(x ) =ex -1 .
x2 -1,x ∈ [0, 2 ], 所以 h ′(x ) =ex -x -1,h ″(x ) =ex -1 .
由 x ∈ [0, 2 ]知,h ″(x ) ≥0,函数 h ′(x )在[0,2 ]上单调递增.
又 h ′(x ) ≥ h ′ (0) =0,所以函数 h ( x ) 在[0,
2 ]单调递增,h (x ) ≥ h (0) =0,即 ex -x - x2 -1≥0,由此可得,f(
x2 -1≥0,由此可得,f(  ) ≥0.
) ≥0.
综 上 所 述, f (
 ) ≤ f ( x0 ) ≤f(
) ≤ f ( x0 ) ≤f( ) .
) .
因为函数 y=f (x )在(0,+ ∞ )上单调递增, 所以 a -1 ≤x0 ≤ 2 ( a -1 ) .
评析 本题给人以亲而不近之感,利用导数判 断函数的单调性、零点个数,并将不等式的证明与零 点的存在性定理完美结合,较好地考查了逻辑推理 能力、转化与化归的思想.
7 反面入手,柳暗花明
例 9 ( 2016 年全国 Ⅰ 卷) 已知函数f( x ) = (x-2 )ex +a (x -1 )2 有两个零点.
( 1 )求 a 的取值范围;
(2 ) 设 x 1,x2 是 f ( x ) 的 两 个 零 点,证 明 :x 1 +x2 <2.
解析 ( 1 ) 显然 1 不是函数f ( x ) 的零点,令
(x-2 )ex +a (x -1 )2 =0,得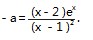
构造函数
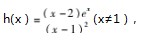
则导函数

由 h ′ (x ) >0 知,x >1;由 h ′ (x ) <0 知,x < 1 .
所以 函 数 h ( x ) 在 ( - ∞,1 ) 单 调 递 减,在 ( 1,+ ∞ )单调递增.
当 x ∈ ( -∞,1 ) ∪ ( 1,2 )时,h(x ) <0;
当 x ∈ (2,+ ∞ )时,h(x ) >0.
综上所述,h(x )的大致图象如图 4 所示.
图 4
因为函数f(x ) = (x -2 ) ex +a (x -1 )2 有两个 零点,所以 y=-a 与 y=h(x ) 图象有两个交点,即 -a <0,解得 a >0.
(2 ) 由(1 )知 x 1 < 1,x2 > 1,不妨假设 x 1 +x2 ≥ 2,则 x2 ≥2-x 1 > 1 .
由函数 h(x )在(1,+ ∞ )单调递增,知 h(x2 ) ≥h(2-x 1 ) .
由 x < 1 知 g′(x ) >0,
即 g(x )在( -∞,1 )上单调递增.
所以 g(x ) < g ( 1 ) =0,即 g (x ) < 0,这与(x- 2 )ex +xe2-x ≥0 矛盾,假设不成立,所以 x 1 +x2 <2.
评析 已知 x 1,x2 是函数f ( x ) 的零点,证明 : x 1 +x2 < m,可以从反面假设 x 1 +x2 ≥m,将问题转 化为比较f(x 1 )与f(m-x 1 )的大小,在此,构造函数 F (x ) =f( x ) -f( m -x ),利用函数的单调性比较 F (x )与 0 的大小,进而推出矛盾. 此方法也可证明 :
x 1 x2 < n.
函数零点的分布是难点,也是近几年高考的热点,综合性很强,考法灵活多变,解题时应该避 重就轻,避实就虚,不失为 一 种明智的策略,可以 考虑以上 7 种策略. 考查了数形结合 、分类讨论 、 函数与方 程 、转 化 与 化 归 数 学 思 想,也 是 解 题 策 略的优 化 与 变 通,更 是“ 临 渊 羡 鱼,不 如 退 而 结 网”的人生境界.
参考文献 :
[ 1 ] 谢新华. 运用数学思想 探究函数零点个数问题 [J ]. 数理化解题研究,2021 (01 ) :29 -30 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/44554.html

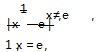 ,若关于 x 的函数 y=f 2 (x ) -mf(x )+m -1(其中 m > 2)有 n 个不同的零点 x 1,x2,x3, …,xn,则f(x 1 +x2 +x3 + …+xn ) = .
,若关于 x 的函数 y=f 2 (x ) -mf(x )+m -1(其中 m > 2)有 n 个不同的零点 x 1,x2,x3, …,xn,则f(x 1 +x2 +x3 + …+xn ) = .
 =1,解得
=1,解得 =m -1,解得
=m -1,解得
 .
. ,此时f ″(x ) =
,此时f ″(x ) = +
+  > 0, 所以f ′(x )在(0,+ ∞ )单调递增.
> 0, 所以f ′(x )在(0,+ ∞ )单调递增. > 0,所以 存在 x0 ∈ (1,2),使得f ′(x0 ) =0.
> 0,所以 存在 x0 ∈ (1,2),使得f ′(x0 ) =0. =0,即 lnx0 =
=0,即 lnx0 = ,所以f(x0 ) =-
,所以f(x0 ) =- -x0,显然f(x0 ) <0.
-x0,显然f(x0 ) <0. ) =(
) =(  -1)ln
-1)ln -
- -1 =
-1 = =0.
=0. ∈ (0,x0 ),
∈ (0,x0 ), ,且两个实根互为倒数.
,且两个实根互为倒数.
 图象交点坐标为 A(x 1,y1 ) .
图象交点坐标为 A(x 1,y1 ) . 图象交点坐标为 B(x2,y2 ) .
图象交点坐标为 B(x2,y2 ) .
 ,所以 x 1 x2 =2020.
,所以 x 1 x2 =2020.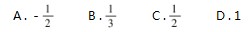
 .
.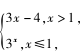 若 a < b,f( a ) =f( b ),求 a+3b 的取值范围 .
若 a < b,f( a ) =f( b ),求 a+3b 的取值范围 .
 若函数 y=f(x ) -m 有四个不同的零点 x 1,x2,x3,x4,满足 x 1 < x2 < x3 < x4,
若函数 y=f(x ) -m 有四个不同的零点 x 1,x2,x3,x4,满足 x 1 < x2 < x3 < x4,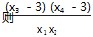 的取值范围是 .
的取值范围是 .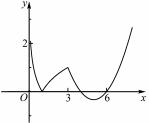
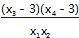 的取值范围是(0,3).
的取值范围是(0,3). ,f(
,f( ))处的切线与 y轴垂直.
))处的切线与 y轴垂直. 过程省略.
过程省略. x +c,令f (x ) =0, 解得-c=x3 -
x +c,令f (x ) =0, 解得-c=x3 - x.
x. x,
x, ) .
) . -或 x >
-或 x > ;
; < x
< x  < .
< . ),(
),(  + ∞ )单调递增,g(x )在( -
+ ∞ )单调递增,g(x )在( -  ,
,  )单调递减.
)单调递减. ) =g( -1 ) = -
) =g( -1 ) = - ,g( -
,g( - ) =g(1 ) =
) =g(1 ) = ,所以 g(x )大致图象如图 3 所示.
,所以 g(x )大致图象如图 3 所示.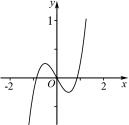
 x 有一个根 x0,由图知 c < -
x 有一个根 x0,由图知 c < - 或 c >
或 c >  ,此时 x0 < -1或 x0 >1,绝对值大于 1,不成立.
,此时 x0 < -1或 x0 >1,绝对值大于 1,不成立. x 有两个根 x 1,x2,由图知 c=-
x 有两个根 x 1,x2,由图知 c=- 或
或 ,此时两根分别为x 1 =-1,x2 =1,绝对值等于 1,成立.
,此时两根分别为x 1 =-1,x2 =1,绝对值等于 1,成立. x 有三个根 x4,x5,x6,由图知 -
x 有三个根 x4,x5,x6,由图知 -  < c <
< c < ,此时 -1 < x4< x5 < x6 <1,绝对值必小于 1,成立.
,此时 -1 < x4< x5 < x6 <1,绝对值必小于 1,成立. ≤x0 ≤
≤x0 ≤ 
 ) ≤0.
) ≤0. ) =e
) =e  -
- -a=e
-a=e -
- -( a -1) -1,
-( a -1) -1, ) ≤0.
) ≤0. ) .
) . ) =e
) =e  -
- -a =e
-a =e -
- -
- ·2(a -1) -1,
·2(a -1) -1, x2 -1,x ∈ [0, 2 ], 所以 h ′(x ) =ex -x -1,h ″(x ) =ex -1 .
x2 -1,x ∈ [0, 2 ], 所以 h ′(x ) =ex -x -1,h ″(x ) =ex -1 . x2 -1≥0,由此可得,f(
x2 -1≥0,由此可得,f(  ) ≥0.
) ≥0. ) ≤ f ( x0 ) ≤f(
) ≤ f ( x0 ) ≤f( ) .
) .