SCI论文(www.lunwensci.com):
摘要:整理和研究高考题发现,有关函数图象考查的选择题在近年高考中经常出现,难度一般中等.这类问题因为蕴含数形结合思想,非常隐蔽地考查函数的各项性质,灵活性很强,命题方式也很开放,所以深受命题专家的青睐.
关键词:函数图象;数形结合;选择题
即题中所给的函数为奇函数,函数图象关于坐标原点对称,据此可知选项CD错误.
且x=π时,y=πcosπ+sinπ=-π<0,据此可知选项B错误.故选A.
例5(2019年全国卷理(新课标Ⅰ)函数f(x)
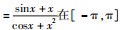 的图象大致为( ).
的图象大致为( ).
 即函数f(x)是偶函数,故排除A,C.
即函数f(x)是偶函数,故排除A,C.
由f(x)=f(x-2),得f(x)=f(x-2)=f(-x),
即函数关于x=-1对称,排除D.故选B.点评与反思根据函数解析式判断函数大致图象,是全国和各省高考的热点,一般以选择题出现,我们需要高度重视.例1-5的解析式明确,例6是抽象函数,没有明确的解析式.这类题的实质是函数性质的变换考查,我们需要从以下方面分析:
(1)从函数定义域考虑,判断图象的左右位置;
(2)从函数的值域考虑,判断图象的上下位置;
(3)从函数单调性考虑,判断图象的变化趋势;
(4)从函数的奇偶性考虑,判断图象的对称性;
(5)从函数的特征点考虑,如与坐标轴的交点,排除不合要求的图象;
(6)从函数的特征线考虑,如对称轴或渐进性,判断函数图象的分布情况;
(7)从极值和拐点考虑,判断函数的行进和弯曲特点.
利用上述方法排除、筛选选项.其中前五项运用较多,后两项考查较少.在解题策略和应试技巧方面,尤其要注意排除法的运用,这是针对选择题的妙法.
2根据函数图象判断可能符合的函数解析式
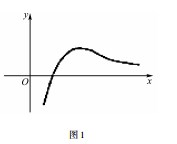
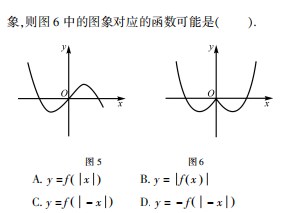
解析 图 6 中的图象是在图 5 的基础上,去掉函数 y = f x( )的图象在 y 轴右侧的部分,然后将 y 轴左侧图象翻折到 y 轴右侧,y 轴左侧图象不变得来的,所以 图 6 中 的 图 象 对 应 的 函 数 可 能 是 y =f( - x ). 故选 C.
例 12 已知下列六个函数:y = x,y = x2,y =lnx,y = 2x,y = sinx,y = cosx,从中选出两个函数记为f( x )和 g ( x ),若 F ( x ) = f( x ) + g ( x )的图象如图 7 所示,则 F ( x ) = .
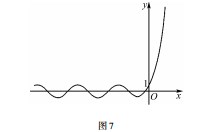
解析 观察图象可知,图象有如下特点,
(1)函数 F ( x )的定义域是 R;
(2)函数 F ( x )过定点(0,1 );
(3)当 x > 0 时,F ( x ) > 1,且单调递增,增大到无穷大;当 x < 0 时,F ( x ) > 0 与 F ( x ) < 0 交替出现;
(4)图象不对称,不具有奇偶性.由(1)直接排除 y = lnx;由(3)知函数 y = 2x 一定要选,并且因为 y = 2x 的图象经过点 0,1 ( ),且当 x> 0 时,y > 1,当 x < 0 时,0 < y < 1,若选 y = cosx,当x = 0 时,y = 1,2x+ cosx 不满足过点 0,1 ( ),所以只有当 F ( x ) = 2x+ sinx 才满足条件(检验). 本题其实也是选择题.
点评与反思根据函数图象判断可能符合图象的函数解析式,其实是第一类问题的逆向考查,只是考查方式不同,考查内容依然是函数的各种性质.这类题高考已经出现,但还没大规模出现,也是我们今后备考的重点.例7-9是最为常见的考查方式,选项的函数解析式明确给出;例11考查函数的图象变换规律,解析式是抽象的;例10和例12是这类问题的创新考查方式,具有开放性的特点.我们的求解策略是观察函数图象的特点,寻找对应函数解析式,具体而言我们需要从以下方面分析:
(1)从图象的左右位置考虑函数的定义域;
(2)从图象的上下位置考虑函数的值域;
(3)从图象的变化趋势考虑函数的单调性;
(4)从图象的对称性考虑函数的奇偶性;
(5)从图象的循环往复考虑函数的周期性;
(6)从图象的特征点考虑函数的零点;
(7)从图象的对称轴或渐进性等考虑函数的结构特征.
如果说第一类问题是从数到形,那么第二类问题其实是从形到数,当然,在解题实践中,数形是结合考虑的,这里只是思维的先后而已.
3在同一个直角坐标系中判断几个函数图象的共存问题
例13(2019年浙江6)在同一直角坐标系中,
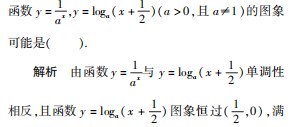 足要求的图象为 D.
足要求的图象为 D.
例14 已知二次函数 y = ax2+ bx + c( a≠0 )的图象如图8 所示,则正比例函数 y = ( b + c)x 与反比例函
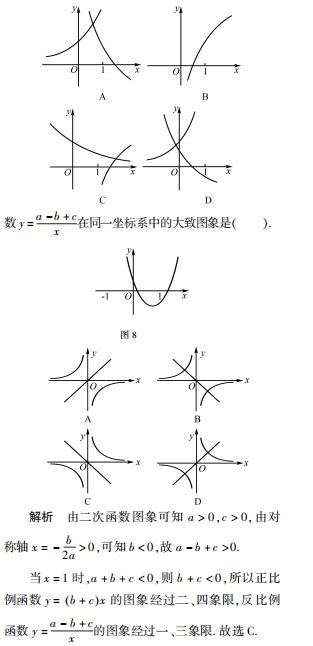
点评与反思 在同一个直角坐标系中判断几个函数图象的共存问题,是基于几个函数解析式里具有相同的参数,当这些参数变化时导致这些函数图象的变化,于是在同一个直角坐标系中几个函数的图象共存就会满足一定的要求,就是有联系的、有条件的共存. 我们的解题思路是分类讨论参数,逐一排除检验. 具体依然是从函数图象的定义域、值域、单调性、特殊点等方面一并考查筛选.
4 根据函数解析式和图象判断参数范围问题

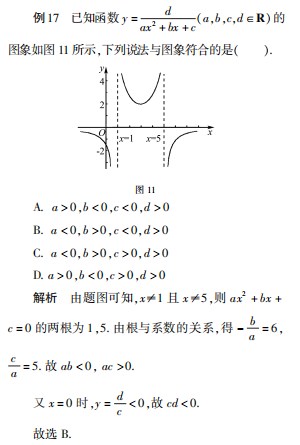
点评与反思 根据函数解析式和图象判断参数范围问题,可以看成是以上三类问题的一个综合考查,安徽高考已经出现,相信这类问题会是以后高考函数考查的常客. 解题策略是结合图象和函数解析式共同分析,确定参数的正负或者范围.以上四类有关函数图象问题的选择题,基本囊括这些问题的所有情况,我们的根本解题策略是数形结合,分类讨论和逐一排除,采用定性分析和定量计算相结合,找到符合条件的函数图象或者函数的解析式. 望此文能给读者带来帮助.
参考文献:
[1] 刘玉文. 2012 年高考函数图象选择题的几种解法[J]. 高中数理化,2013(07):16 - 17.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/47819.html
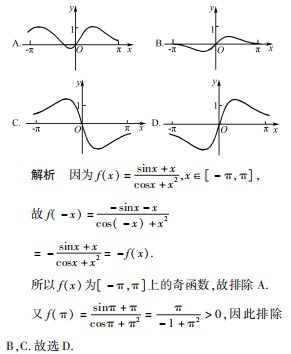
 在[-6,6]的图象大致为().
在[-6,6]的图象大致为().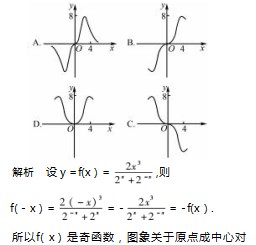 称 ,排除选项 C.
称 ,排除选项 C. 所以 f(x)为奇函数,舍去 A.
所以 f(x)为奇函数,舍去 A.

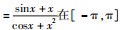 的图象大致为( ).
的图象大致为( ).





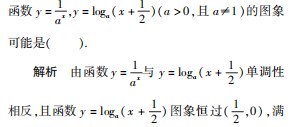 足要求的图象为 D.
足要求的图象为 D.



