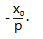SCI论文(www.lunwensci.com):
摘 要 :文章通过对 2021 年安徽省冬季联赛第22 题的解法探究,得到了相关研究对象在运动 变化过程中保持的规律性及其变式推广,并由试题的解答与变式得出了关于圆锥曲线的一 个统一 结论,从而揭示了问题的本质和规律.
关键词 :冬季联赛;解法探究;共轭弦性质;圆锥曲线
1 试题呈现
题目 (安徽省示范高中培优联盟 2021 年冬季联赛 (高二) 第 22 题) 已知椭圆 C :

+

= 1 ( a > b >0 )的长轴长为 4 2,离心率为C

.
(1)求椭圆 C 的标准方程;
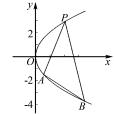
(2)已知斜率为

的直线 l 与椭圆 C 交于两个不同的点 A,B,点 P 的坐标为 (2,1 ),设直线 PA 与 PB 的倾斜角分别为 α,β,证明:tanα+tanβ=0.
试题第(1)问考查了椭圆的长轴、离心率等简 单的几何性质,体现了试题的基础性;第(2)问以圆 锥曲线共轭弦性质为背景设置了与动直线有关的定 值问题,综合性强,对学生逻辑推理、数学运算、直观 想象等素养有较高要求,值得深入探究.
2 解法探究
第(1)问椭圆 C 的标准方程为

+

=1(过程略),下面探究第(2)问的解法.
证法 1 当直线 l 过原点时,点 P( 2,1 )在直线 l :y=
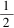
x 上,不符合题意.
故设直线 l 方程为 y=

x +t ( t≠0 ),A ( x 1,y1 ),B ( x2,y2 ),联立
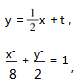
得
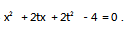
则

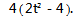
由于直线l 与椭圆 C 相交于 A,B 两点,因此 Δ >0,即 t ∈ ( -2,0 ) ∪ ( 0,2 ),此时,直线 PA,PB 的斜率都 存在,所以,要证 tanα+tanβ=0,即证 kPA +kPB =0.
所以 kPA +kPB =0. 即 tanα+tanβ=0.
点评 证法 1 把待证问题转化为求证两直线 PA,PB 斜率之和为 0,从而几何问题通过坐标运算 转化为代数问题,既展示了坐标法的魅力,又体现了数形结合的思想. 继续探究,如图 1,发现当 Δ =0时,t=-2 或 t =2,此时直线 l 与椭圆 C 相切,点 P 坐标为( -2,1 )或 (2,-1 ),直线 l 的斜率与椭圆 C在点 P 处的切线的斜率互为相反数,这一发现为进 一步探究试题本质提供了思路.
图 1
证法 2 设直线 PA 的参数方程为

( t 为参数),
代入椭圆 C :

+

=1,得( 1 +3 sin2 α )t2 +4 ( cosα+2sinα )t=0.则

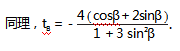
由题意,得
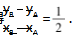
即 2 ( yB -yA ) =xB -xA .
所以 tB ( 2 sinβ-cosβ ) =tA ( 2 sinα -cosα ).
代入 tA,tB 有-

· ( 2sinβ-cosβ) =
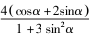
- · ( 2sinα-cosα ).
整理,得
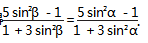
化简,得sin2 α =sin2β.
由于 0 <α <π,0 <β <π,且 α≠β,所以 α=π-β. 从而 tanα+tanβ=0.
点评 证法 2 从直线 PA 与 PB 的倾斜角入手, 自然联系到应用直线的参数方程解题,亮点在于对 坐标的处理,借助参数的意义和三角恒等变换,整个运算过程一气呵成,简洁明了.
证法 3 作平移变换 τ:
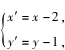
则变换后的椭圆方程为
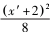
+

=1 .
整理,得 x ′2 +4y′2 +4 ( x ′+2y′) =0.
设直线 AB 的方程为 mx ′-2my′ =1,代入上式,得x ′2 +4y′2 +4m ( x ′+2y′ ) (x ′-2y′ ) =0. 即( 1 +4m )x ′2 + (4 -16m )y′2 =0.
两边同时除以 x ′2,得
(4 -16m )

+1 +4m=0. ①
由于平移变换后点 P 的坐标变为 P′( 0,0 ),故 kP′A′,kP′B′是方程①的两个根,由韦达定理知 kP′A′ + kP′B′ =4-6m=0,由于平移变换下不改变直线的斜 率,所以 kPA +kPB =0.
点评 证法 3 通过平移变换巧妙地把椭圆上的 定点 P 转化为坐标原点 P′,变换后两直线 P′ A′, P′B′的斜率恰好是点 A′,B′的坐标比值,从而通过齐 次化处理,把两直线斜率之和问题转化为韦达定理 根与系数的关系,解答简洁明了,相比通性通法中运 算量大的特点,平移变换后齐次化处理很大程度上 避免了繁杂的运算,是解答过定点两条动直线斜率之积、之和问题的利器.
证法4 设直线 PA 的方程为 y -1 =k1 ( x-2), 直线 PB 的方程为 y -1 =k2 ( x-2),于是过点 P,A, B 的曲线系方程为[k1 (x-2) -(y -1 ) ] [ k2 (x -2)-(y -1) ] +λ + -1 =0. ②.
又椭圆 C :

+

=1 在点 P (2,1)处的切线方程为 x +2y-4 =0,由题意知直线 AB 的方程可设为 x-2y+m=0,则曲线系方程②等价于
( x +2y-4) (x-2y+m ) =0. ③
切线 x +2y-4 =0 上任取异于点 P 的一点,不 妨取 x =0,y=2 代入②得 λ= -(1 +2k1 ) (1 +2k2 ).
比较方程②③中 x2,y2 的系数,得
1 =k1 k2 -

(1 +2k1 ) (1 +2k2 ),
-4 =1 -

(1 +2k1 ) (1 +2k2 ).
即

从而 k1 +k2 =0. 即 tanα+tanβ=0.
点评 证法 4“曲线系方程法”相比前面证法, 站在更高的观点,为我们解决这类解析几何问题提 供了新视角,但也有一定的局限性,在具体的解题实 践中,还需根据自身实际,选择适当的方法.
3 推广探究
著名数学教育家 G · 波利亚说“分解和重组是 思维的重要活动”,因此我们有必要深入到试题的 细节中去,通过逆向变换,亦或者改变曲线背景提出新 的问题,以探究试题内在规律,培养学生思维品质.
变式 1 已知 A,B 为椭圆 C :

+

=1 上的两个动点,点 P(2,1),若直线 PA 的斜率与 PB 的斜率 互为相反数,证明直线 AB 的斜率为定值.
证明 设 A ( x 1,y1 ),B ( x2,y2 ),椭圆

+

=1写为
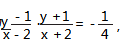
所以 kPA =

=-

·

,
kPB =
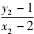
=-

·

.
由 kPA +kPB =0,得

-

·

=0,
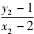
-

·

=0.
分别整理,得
4y1 y2 +4y1 -4y2 =x 1 x2 +2x 1 -2x2 ..④
4y1 y2 +4y2-4y1 =x 1 x2 +2x2-2x 1 . ⑤,
④-⑤,得 8y1 -8y2 =4x 1 -4x2 .
即有 kAB
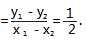
当直线 PA,PB 的斜率互为相反数时,我们发现 直线 AB 的斜率与椭圆 C 在点 P 处的切线的斜率互 为相反数,也就是说点 P 的位置唯一决定了 AB 的 斜率,反过来 AB 的斜率也唯一决定点 P 的坐标.
推广 1 设点 P ( x0,y0 )是椭圆 C :

+

= 1( a > b >0)上一定点,A,B 是椭圆 C 上两个动点,若 直线 PA,PB 的斜率互为相反数,则直线 AB 的斜率
存在时,kAB =
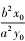
.
证明 作平移变换 τ :
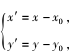
则变换后的椭圆方程为
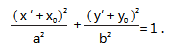
整理,得 b2 x ′2 +a2 y′2 +2x0 b2 x ′+2y0 a2 y′=0. 设直线 AB 的方程为 mx ′+ny′ =1,
代 入 上 式, 得 ( b2 +2mx0 b2 ) x ′2 + ( a2 + 2ny0 a2 )y′2 +2(nx0 b2 +my0 a2 )x ′y′=0. 两边同时除以 x ′2,得(记 k ′=

)
( a2 +2ny0 a2 ) k ′2 + 2 ( nx0 b2 +my0 a2 ) k ′ + b2 +2mx0 b2 =0.
由题意知,kP′A′,kP′B′ 是方程⑥的两个根,且 kP′A′ +kP′B′ =0,故 nx0 b2 +my0 a2 =0.
所以 kAB =
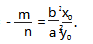
变式 2 如图 2,点 P ( x0,y0 ) (y0 >0 )为抛物线 C :y2 =2px (p >0 )上一定点,A ( x 1,y1 ),B ( x2,y2 )为抛物线 C 上两动点,若直线 PA 与 PB 斜率存在且互 为相反数,求证 :直线 AB 的斜率是非零常数.
图2
证明 因为点 P ( x0,y0 ),A ( x 1,y1 ),B ( x2,y2 )在抛物线 y2 =2px 上,所以

=2px0 ⑨.
⑦-⑧,得(y0 -y1 ) (y0 +y1 ) =2p ( x0 -x 1 ).
即 kPA =
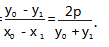
同理可得 kPB =
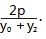
由 kPA +kPB =0,得

+

=0.
即有 y1 +y2 =-2y0 .
⑨-⑧,得(y2 -y1 ) (y2 +y1 ) =2p ( x2 -x 1 ).
即 kAB =

变式 3 已知直线 l :y=-4x +m 与双曲线 E :

-

=1 的右支交于不同两点 A. B,点 Q (2,2 ),
记直线 QA,QB 的斜率分别为k1 . k2,求证 :k1 +k2 =0.
证明 作平移变换 τ:
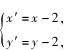
则变换后的双曲线方程为

-

=1 .
整理,得 4x ′2 -y′2 +16x ′-4y′=0. ⑩
设直线 l ′的方程为 px′ +qy′ =1(其中 p =4q), 代入⑩式,得4x ′2 -y′2 + ( 16x ′-4y′ ) (px ′+qy′ ) =0.
即(4 +16p )x ′2 -( 1 +4q )y′2 =0.
两边同时除以 x ′2,得
-( 1 +4q )+4

+16p =0.
由于平移变换后点 Q 的坐标变为 Q′( 0,0 ),故 kQ′A′,kQ′B′是方程的两个根.
由韦达定理知 kQ′A′ +kQ′B′

=0
由于平移变换下不改变直线的斜率, 所以 k1 +k2 =0.
推广 2 设点 P( x0,y0 )是对称轴平行于坐标轴 的定圆锥曲线(包括圆、椭圆、双曲线和抛物线) C 上一定点,A,B 是 C 上两个动点,若直线 PA,PB 的 斜率互为相反数,则直线 AB 的斜率存在时为定值, 等于曲线 C 在点 P 处切线的斜率的相反数.
(1)当曲线 C 是有心圆锥曲线时,设方程统一形式为 λx2 +μy2 =1(λμ≠0),则 kAB =

( y0 ≠0 );
(2)当曲线 C 是抛物线时,可设 C :y2 =2px(p ≠0),则 kAB =-
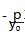
或 C :x2 =2py(p≠0),则 kAB =
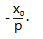
推广 2 也称为圆锥曲线共轭弦性质,以其为背 景命制的高考试题和竞赛试题屡见不鲜,像这样通 过挖掘改造著名数学问题来命题已成为近年高考数 学圆锥曲线压轴题命制的新趋势,这也启示一线教 师在教学中应充分利用这些素材,引导学生探究试 题解法,剖析试题本质,从而培育学生的思维品质, 落实学科素养.
参考文献 :
[ 1 ] 波利亚,涂泓译. 怎样解题—数学思维的新方 法 [ M ] . 上海 :上海科技教育出版社,2007 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/45060.html
 +
+ = 1 ( a > b >0 )的长轴长为 4 2,离心率为C
= 1 ( a > b >0 )的长轴长为 4 2,离心率为C .
. 的直线 l 与椭圆 C 交于两个不同的点 A,B,点 P 的坐标为 (2,1 ),设直线 PA 与 PB 的倾斜角分别为 α,β,证明:tanα+tanβ=0.
的直线 l 与椭圆 C 交于两个不同的点 A,B,点 P 的坐标为 (2,1 ),设直线 PA 与 PB 的倾斜角分别为 α,β,证明:tanα+tanβ=0. +
+  =1(过程略),下面探究第(2)问的解法.
=1(过程略),下面探究第(2)问的解法.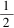 x 上,不符合题意.
x 上,不符合题意. x +t ( t≠0 ),A ( x 1,y1 ),B ( x2,y2 ),联立
x +t ( t≠0 ),A ( x 1,y1 ),B ( x2,y2 ),联立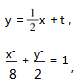 得
得 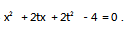

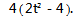
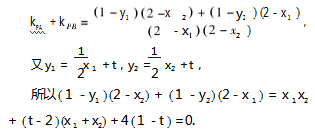

 ( t 为参数),
( t 为参数), +
+ =1,得( 1 +3 sin2 α )t2 +4 ( cosα+2sinα )t=0.则
=1,得( 1 +3 sin2 α )t2 +4 ( cosα+2sinα )t=0.则 
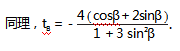
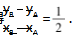
 · ( 2sinβ-cosβ) =
· ( 2sinβ-cosβ) = 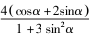 - · ( 2sinα-cosα ).
- · ( 2sinα-cosα ).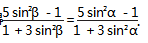
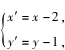
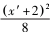 +
+ =1 .
=1 . +1 +4m=0. ①
+1 +4m=0. ① +
+  =1 在点 P (2,1)处的切线方程为 x +2y-4 =0,由题意知直线 AB 的方程可设为 x-2y+m=0,则曲线系方程②等价于
=1 在点 P (2,1)处的切线方程为 x +2y-4 =0,由题意知直线 AB 的方程可设为 x-2y+m=0,则曲线系方程②等价于 (1 +2k1 ) (1 +2k2 ),
(1 +2k1 ) (1 +2k2 ), (1 +2k1 ) (1 +2k2 ).
(1 +2k1 ) (1 +2k2 ).
 +
+ =1 上的两个动点,点 P(2,1),若直线 PA 的斜率与 PB 的斜率 互为相反数,证明直线 AB 的斜率为定值.
=1 上的两个动点,点 P(2,1),若直线 PA 的斜率与 PB 的斜率 互为相反数,证明直线 AB 的斜率为定值. +
+ =1写为
=1写为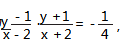
 =-
=- ·
· ,
,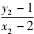 =-
=- ·
· .
. -
- ·
· =0,
=0,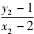 -
- ·
· =0.
=0.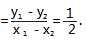
 +
+ = 1( a > b >0)上一定点,A,B 是椭圆 C 上两个动点,若 直线 PA,PB 的斜率互为相反数,则直线 AB 的斜率
= 1( a > b >0)上一定点,A,B 是椭圆 C 上两个动点,若 直线 PA,PB 的斜率互为相反数,则直线 AB 的斜率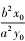 .
.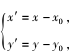
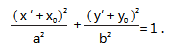
 )
)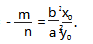
 =2px0 ⑨.
=2px0 ⑨.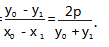
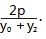
 +
+ =0.
=0.
 -
- =1 的右支交于不同两点 A. B,点 Q (2,2 ),
=1 的右支交于不同两点 A. B,点 Q (2,2 ),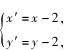
 -
- =1 .
=1 . +16p =0.
+16p =0.  =0
=0 ( y0 ≠0 );
( y0 ≠0 );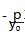 或 C :x2 =2py(p≠0),则 kAB =
或 C :x2 =2py(p≠0),则 kAB =