SCI论文(www.lunwensci.com):
摘要:文章围绕2022届高三八省联考中的圆锥曲线大题进行研究,通过不同角度的探究,给出了该问题的5种解题方法,并进一步作了相应的方法总结,然后在课本中找出该题的“题根”,最后对此题还进行了推广拓展和变式探究.
关键词:八省联考;圆锥曲线;解法探究;课本溯源;拓展推广
2022年高三八省联考试卷第21题是一道新颖的解析几何大题,它采用开放性的二选一题型,给了学生很大的自由发挥空间.主要考查了圆锥曲线方程求解、四边形面积最值、三等分点问题,试题稳中求新,体现了考题的基础性、综合性、创新性,考查了学生数学运算、逻辑推理、直观想象等核心素养和关键能力,本文从该题的解法探究入手,然后再回到课本中追本溯源,最后对此题进行一般化推广和变式探究,以期对教学、研究、学习提供帮助.
1试题呈现
(1)求Γ的方程;
(2)如图1,过原点O作互相垂直的直线l1,l2,分别交双曲线于A,B两点和C,D两点,点A,D在x轴同侧,请从①②两个问题中任选一个作答:①求四边形ABCD面积的取值范围;②设直线AD与两渐近线分别交于M,N两点,是否存在直线AD使M,N为线段AD的三等分点,若存在,求出直线AD方程;若不存在,说明理由.
2解法探究
探究思路1(1)题难度不大,略.对于(2)题,选择①,求四边形ABCD面积的取值范围时,其通解通法是使用函数法,考虑利用直线AB的斜率来表示四边形的面积.
故四边形ACBD面积的取值范围为[6,+∞).探究思路3此题还可使用齐次化法,从而构造出两条直线的斜率,利用垂直得到关键等式.
解析3设AD:mx+ny=1,与双曲线构造齐次:
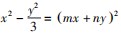
,整理,得
 探究思路4此题两条直线都经过原点这个定点,故考虑利用直线参数方程来求弦长.
探究思路4此题两条直线都经过原点这个定点,故考虑利用直线参数方程来求弦长.
解析4设直线AB的参数方程为

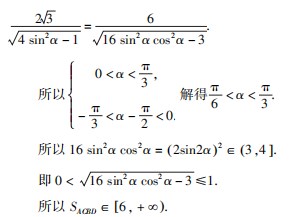 探究思路5题中直线AB和直线CD都经过原点,这里还可使用极坐标方程来求弦长.
探究思路5题中直线AB和直线CD都经过原点,这里还可使用极坐标方程来求弦长.
3追本溯源
这道八省八校解析几何大题使用的方法多样,其实课本早有铺垫,它严格地贯彻了源于教材,高于教材的命题原则.它与人教版选修4-4中第15页习题有着很大的相似性:
已知椭圆的中心为O,长轴、短轴的长分别为2a,2b(a>b>0),A,B分别为椭圆上的两点,且OA⊥OB.
 (2)求△AOB面积的最大值和最小值.
(2)求△AOB面积的最大值和最小值.
由此启发我们在教学中要回归教材,一要让教材和教辅资料各尽其责、物尽其用,防止本末倒置;二要重视教材中在知识发生和发展中呈现的那些经典的思维模式;三要注意挖掘教材中例题习题背后广泛而深远的意义,提炼更深层次的公式和结论,使学生深化相关知识.
4推广探究经
深入思考,通过纵向、横向和逆向的方法进行探究,得到此试题有如下拓展推广结论:
结论1经过原点作两条互相垂直的直线交双曲线
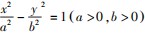 于四点,则此四点围成的四边形的面积的取值范围是
于四点,则此四点围成的四边形的面积的取值范围是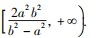
证明以原点为极点,x轴的正半轴为极轴建立极坐标系,两条直线交双曲线于A,B和C,D四点,设
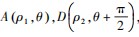 因双曲线极坐标方程
因双曲线极坐标方程
 结论2经过原点作两条互相垂直的直线交椭圆
结论2经过原点作两条互相垂直的直线交椭圆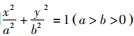 于四点,则此四点围成的四边形的面积的取值范围是
于四点,则此四点围成的四边形的面积的取值范围是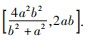
结论4经过原点作两条垂直的直线交双曲线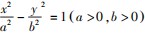 于A,B和C,D四点,并过原点作OE⊥AD,垂足为点E,则OE必为定值
于A,B和C,D四点,并过原点作OE⊥AD,垂足为点E,则OE必为定值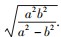
事实上,因OE为定值,故点O在直线AD上的射影是以O为圆心,以
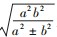
为半径的圆,这里我们把这个圆命名为双曲线或椭圆的基圆.并且此圆恰为四边形ABCD的内切圆,由此可得下面的结论5:
结论5已知圆锥曲线
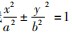
,直线l是圆x2+y2=r2的任意一条切线,与圆锥曲线交于A,B两点,则OA⊥OB的充要条件是r=
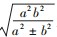
结论6经过椭圆
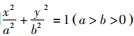
的左焦点作两条互相垂直的直线交椭圆于A,B和C,D四点,则此四点围成的四边形的面积的取值范围是

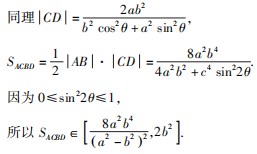 5链接高考
5链接高考
题1(2016年高考全国Ⅰ卷理数20题)设圆x2+y2+2 x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过点B作AC的平行线交AD于点E,设点E轨迹为曲线C 1,直线l交C 1于M,N两点,过点B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
题2(2013年高考Ⅱ卷理数20题)过椭圆
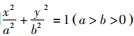
右焦点的直线x+y-
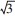
=0交椭圆于A,B两点,P为AB的中点,且OP的斜率为

又C,D是椭圆上两点,且CD⊥AB,求四边形ABCD面积的最大值.
综上所述,解析几何综合题通常基于几何性质或定理出发,通过特殊化,变更条件和结论来命题,特别对椭圆和抛物线的对偶性质,教师要挖掘问题的本质和内涵思想方法,要研究习题的变式推广,发展学生思维;要研究一题多解,培养学生的创新意识.
参考文献:
[1]肖骁.揭开面纱还原本质—二道高考试题赏析[J].福建中学数学,2014(05):14-16.
[2]罗增儒.解题分析—人人都能做解法的改进[J].中学数学教学参考,1998(07):29-30.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/44789.html

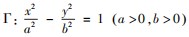 过点
过点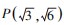 且Γ的渐近线方程为y=
且Γ的渐近线方程为y=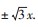
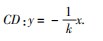


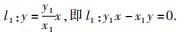

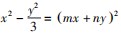 ,整理,得
,整理,得

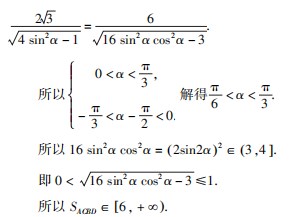
 ,因双曲线极坐标方程为
,因双曲线极坐标方程为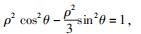


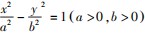 于四点,则此四点围成的四边形的面积的取值范围是
于四点,则此四点围成的四边形的面积的取值范围是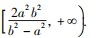
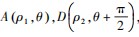 因双曲线极坐标方程
因双曲线极坐标方程
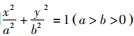 于四点,则此四点围成的四边形的面积的取值范围是
于四点,则此四点围成的四边形的面积的取值范围是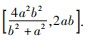
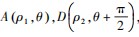 因椭圆极坐标方程为
因椭圆极坐标方程为
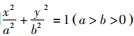 于A,B和C,D四点,并过原点作OE⊥AD,垂足为点E,则OE必为定值
于A,B和C,D四点,并过原点作OE⊥AD,垂足为点E,则OE必为定值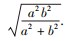


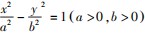 于A,B和C,D四点,并过原点作OE⊥AD,垂足为点E,则OE必为定值
于A,B和C,D四点,并过原点作OE⊥AD,垂足为点E,则OE必为定值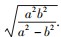
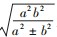 为半径的圆,这里我们把这个圆命名为双曲线或椭圆的基圆.并且此圆恰为四边形ABCD的内切圆,由此可得下面的结论5:
为半径的圆,这里我们把这个圆命名为双曲线或椭圆的基圆.并且此圆恰为四边形ABCD的内切圆,由此可得下面的结论5: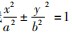 ,直线l是圆x2+y2=r2的任意一条切线,与圆锥曲线交于A,B两点,则OA⊥OB的充要条件是r=
,直线l是圆x2+y2=r2的任意一条切线,与圆锥曲线交于A,B两点,则OA⊥OB的充要条件是r=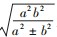
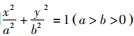 的左焦点作两条互相垂直的直线交椭圆于A,B和C,D四点,则此四点围成的四边形的面积的取值范围是
的左焦点作两条互相垂直的直线交椭圆于A,B和C,D四点,则此四点围成的四边形的面积的取值范围是
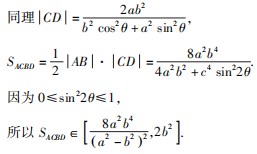
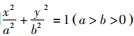 右焦点的直线x+y-
右焦点的直线x+y-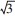 =0交椭圆于A,B两点,P为AB的中点,且OP的斜率为
=0交椭圆于A,B两点,P为AB的中点,且OP的斜率为 又C,D是椭圆上两点,且CD⊥AB,求四边形ABCD面积的最大值.
又C,D是椭圆上两点,且CD⊥AB,求四边形ABCD面积的最大值.