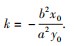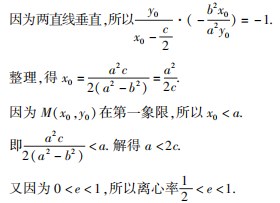SCI论文(www.lunwensci.com):
摘 要 :本文将圆锥曲线的离心率问题按知识点进行分类,对同类型的题 目给出了类似的、相 对简单的解法,并进行了深层次的剖析,目 的是使学生能迅速将问题归类、抓住关键,找到数学本 源,从而由点到面突破,培养学生的数学核心素养.
关键词 : 离心率;范围;特殊三 角形;平行四边形;圆
圆锥曲线离心率问题通常是指椭圆和双曲线的 离心率问题,一般包含两类:一是求离心率值;二是求离心率的取值范围. 求解离心率,一般是构造参数 a,c 或 a,b 等式或者不等式,找出它们的关系,从而 计算. 离心率问题难点不在求解,而在找等量关系或 者不等量关系,也就是找出题目中的数学本源. 如何 能在最短的时间内,找到关系,最有效的办法是从数学本源出发,研究命题方向和结合的知识点,发现规 律,探究方法,形成一系列解题策略.
1 特殊三角形与离心率
这类题目通常利用特殊三角形的性质来找参数 关系,用到的性质一般有边角相等、三角形相似、面 积公式、正余弦定理、角平分线性质、高的性质、中线 的性质等,解题方法可用代数法也可用几何法,通常 数形结合,用几何法计算量较小,运算相对简单.
例 1 双曲线
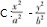
= 1 ( a > 0,b > 0) 的左
右焦点分别为 F1,F2,离心率为 e,过点 F2 的直线交双曲线的右支于 A,B 两点,若△F1 AB 是不以点 F1 为直角顶点的等腰直角三角形,则 e2 等于 .
解析 因为顶点 A,B 在双曲线上,由双曲线的 定义,可得到含四个参量的两个等式,结合等腰直角 三角 形 这 个 条 件,可 以 消 掉 两 个 参 量,再 利 用 Rt△F1 BF2 解出 BF1,BF2 的值.
图 1
如图 1,不妨设点 B 是 Rt△F1 AB 的直角顶点,则
AF1= 2AB= 2BF1 .
又点 A,B 在双曲线上,由双曲线的定义,得 AF1-AF2 =2a,BF1 -BF2 =2a. ②
联立①②,得 BF1 =2 2 a,BF2 =2 2 a-2a. 在 Rt△F1 BF2 中,由勾股定理,得
2 平行四边形与离心率
与平行四边形结合的离心率问题一般有两类, 一类是题目中存在四边形;另一类是利用圆锥曲线 的对称性构造四边形. 用到的性质通常有 :对边平行 相等;两条对角线长度的平方和等于两倍的两个邻 边的平方和等. 解题时可用代数法也可用几何法.
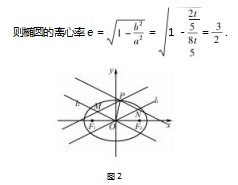
例 2 如图 2,椭圆
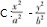
=1 ( a > b >0 ),直 线 l1 :y=-

x,直线 l2 :y =
 x,P 为椭圆上任意一点,过 点 P 作 PM//l1 且 与 直 线 l2 交 于 点 M,作 PN//l2 交 l1 于点 N,若 PM 2 + PN 2 为定值,则 椭圆的离心率为 .
x,P 为椭圆上任意一点,过 点 P 作 PM//l1 且 与 直 线 l2 交 于 点 M,作 PN//l2 交 l1 于点 N,若 PM 2 + PN 2 为定值,则 椭圆的离心率为 .
解析 因为 PM 2 + PN 2 是定值,而式子中 的两个线段长度不好表示,所以可以利用平行四边 形的对称性进行转化. 点 P 在椭圆上,坐标满足椭 圆方程,于是想到把定值转化成与点 P 坐标有关的量, 代入椭圆方程,就找到了一个有关参数的等量关系.
设 PM
2+PN
2 = t 为 定 值,M ( x1,
 x 1 ), N(x2,-
x 1 ), N(x2,- x2 ),顶点 P(x,y),因为四边形 PMON 是平行四边形,所以
x2 ),顶点 P(x,y),因为四边形 PMON 是平行四边形,所以
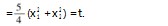
3 圆与离心率
借助于圆的性质求离心率问题的题目相对较 多,考查点通常是圆的性质和圆锥曲线性质的结合, 比如弦的中点与圆心的连线与弦垂直,直径所对的 圆周角是 90°,半径相等,圆与圆的位置关系等.
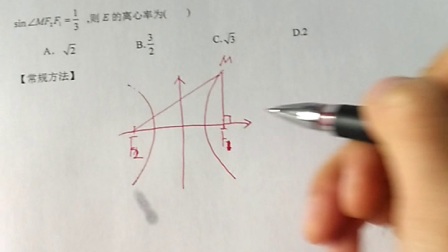
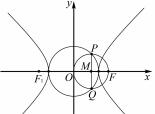
例 3 如图 3,设点 F 为双曲线
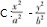
=1(a
>0,b > 0)的右焦点,O 为坐标原点,以 OF 为直径 的圆与圆 x2 + y2 = a2 交于 P,Q 两点. 若 PQ = OF ,则 C 的离心率为 .
解析 两圆的半径分别有参数 a,c,找 a,c 的关 系,只需找两圆的关系即可. 解题方法可以用代数法 也可用几何法,但几何法要相对简单.
由对称性可知 PQ⊥x 轴,因为 OF 是圆的直径, 且 PQ = OF ,所以 PQ 也是圆的直径.
所以 OM=PM=
 OF=
OF= c.
c.
所以△POM 是直角三角形.
于是有 OP2 =OM2 +PM2 .
 4 变量的范围与离心率
4 变量的范围与离心率
该类题目通常是先给出标准方程中某个参数的 范围,或者变量的范围,再结合具体图形的平行关 系、共线关系、垂直关系等求离心率的取值范围. 通常用代数法来求解.
图 3
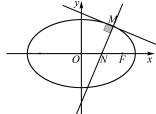
例 4 如图 4,椭圆
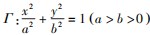
的
离心率为 e,F 是 Γ 右焦点,点 P 是 Γ 上第一象限内 任意一点,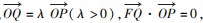 ,若 λ < e,则 e 的取值范围是 .
,若 λ < e,则 e 的取值范围是 .
图 4
解析 已知参数λ <e,所以要根据已知条件表示 出参 数 λ 的 值,因 为 点 P 在 第 一 象 限 且 = λ (λ >0),所以要先表示出点 P 的坐标. 设∠POF=θ (0 < θ < ),由 · =0 得 OP⊥FQ. 所以 OQ = OF ·cosθ. 点 Q 的坐标为 Q(ccos2 θ,csinθcosθ ). 又=λ (λ >0),得点
解析 由题可知
 切线的斜率为
切线的斜率为 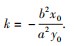
图 5
总之,对于比较复杂的离心率问题,找出等量关 系或者不等关系是关键,通常会与很多知识结合起 来,有时还涉及数形结合. 对于一些常见公式,应该 引导学生自主观察、独立思考,把不熟悉的问题转化 为熟悉的问题,找出数学本源,从而更有效、简洁地 解决它,培养学生的数学核心素养.
参考文献 :
[ 1 ] 范军. 圆锥曲线离心 率的求法[ J ] . 数理天地 (高中版),2020 ( 10 ) :25 -26 .
[2 ] 吴一哲,韩天禧. 例谈离心 率的求法[ J ] . 新高 考,2011 (02) :31 -33 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/44672.html
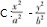 = 1 ( a > 0,b > 0) 的左右焦点分别为 F1,F2,离心率为 e,过点 F2 的直线交双曲线的右支于 A,B 两点,若△F1 AB 是不以点 F1 为直角顶点的等腰直角三角形,则 e2 等于 .
= 1 ( a > 0,b > 0) 的左右焦点分别为 F1,F2,离心率为 e,过点 F2 的直线交双曲线的右支于 A,B 两点,若△F1 AB 是不以点 F1 为直角顶点的等腰直角三角形,则 e2 等于 .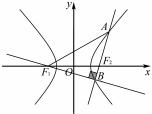
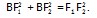

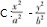 =1 ( a > b >0 ),直 线 l1 :y=-
=1 ( a > b >0 ),直 线 l1 :y=- x,直线 l2 :y =
x,直线 l2 :y = x,P 为椭圆上任意一点,过 点 P 作 PM//l1 且 与 直 线 l2 交 于 点 M,作 PN//l2 交 l1 于点 N,若 PM 2 + PN 2 为定值,则 椭圆的离心率为 .
x,P 为椭圆上任意一点,过 点 P 作 PM//l1 且 与 直 线 l2 交 于 点 M,作 PN//l2 交 l1 于点 N,若 PM 2 + PN 2 为定值,则 椭圆的离心率为 . x 1 ), N(x2,-
x 1 ), N(x2,- x2 ),顶点 P(x,y),因为四边形 PMON 是平行四边形,所以
x2 ),顶点 P(x,y),因为四边形 PMON 是平行四边形,所以
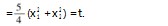
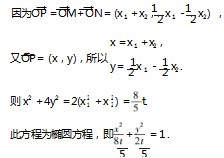
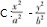 =1(a>0,b > 0)的右焦点,O 为坐标原点,以 OF 为直径 的圆与圆 x2 + y2 = a2 交于 P,Q 两点. 若 PQ = OF ,则 C 的离心率为 .
=1(a>0,b > 0)的右焦点,O 为坐标原点,以 OF 为直径 的圆与圆 x2 + y2 = a2 交于 P,Q 两点. 若 PQ = OF ,则 C 的离心率为 .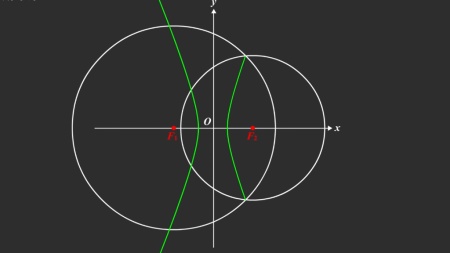
 OF=
OF= c.
c.
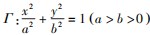 的离心率为 e,F 是 Γ 右焦点,点 P 是 Γ 上第一象限内 任意一点,
的离心率为 e,F 是 Γ 右焦点,点 P 是 Γ 上第一象限内 任意一点,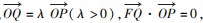 ,若 λ < e,则 e 的取值范围是 .
,若 λ < e,则 e 的取值范围是 .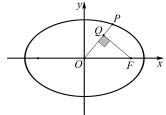

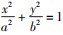 ( a >0,b >0 )上,使得过点 M 且与椭圆在此点的切线
( a >0,b >0 )上,使得过点 M 且与椭圆在此点的切线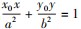 垂直的直线经过点
垂直的直线经过点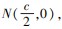 c 为椭圆半焦距,则椭圆的离心率的取值范围是
c 为椭圆半焦距,则椭圆的离心率的取值范围是 切线的斜率为
切线的斜率为