SCI论文(www.lunwensci.com):
摘要:本文例析含参数的函数不等式恒成立求参数范围问题的解题策略,提高学生分析和解决函数综合问题的能力,促进学生数学学科核心素养的达成.
关键词:函数不等式;恒成立;参数范围;解题策略
近年来,全国高考试题及高考模拟试题中出现了颇有新意、构思精巧的函数不等式恒成立求参数范围的综合题,这类题涉及知识面广、综合性强,对能力要求较高,能较好地考查学生的思维能力,很值得重视和探究.
1特值探路
解析将x取特殊值1代入不等式中,不等式应该成立,即f(1)≥1,也即a+lna≥1.
令g(a)=a+lna-1,易知函数g(a)单调递增,g(1)=0,所以a≥1.
下面证明充分性:
 若 x∈(0,1)时,h′(x) < 0;
若 x∈(0,1)时,h′(x) < 0;
若 x∈(1, + ∞)时,h′(x) > 0,
故 h(x)≥h(1) = 1.
所以 a 的范围是[1, + ∞).
点评 利用特殊值探路可以迅速化解题目难 度,快速找到题目的答案(准答案),减轻解题思想 压力,转换解题思维角度,补全充分性证明过程即可 完美收官. 一般对数函数可将真数取特值 1,指数函 数的指数可取特值 0.
2 分类筛选
例 2 设函数 f( x) = ax + cosx,x∈[0,π],设 f(x)≤1 + sinx,求 a 的取值范围.

 点评 含参数函数不等式恒成立求参数范围问 题可以利用逐段筛选讨论法求解,对参数按照重要 节点进行分类,在每一类中证明不等式成立或举反 例说明不成立,最后得解,体现了化整为零的思想和 归类整理的思想.
点评 含参数函数不等式恒成立求参数范围问 题可以利用逐段筛选讨论法求解,对参数按照重要 节点进行分类,在每一类中证明不等式成立或举反 例说明不成立,最后得解,体现了化整为零的思想和 归类整理的思想.
3 分离参数
例 3 设函数 f(x) = ax + cosx,x∈[0,π],设 f(x)≤1 + sinx,求 a 的取值范围


点评 不等式恒成立求参数范围问题,只要容 易实现参变分离,就可以很容易转化为最值(或上、 下界)问题求解,但在求最值(或上、下界)时常常要 用到洛必达法则.
4 构造函数

 点评 在含参数函数不等式恒成立求参数 范围问题中,将不等式两边转化成同构式,根据 同构式构造新函数,利用新函数单调性进一步转 化问题,使得问题得到降维求解,此法虽然有一 定难度,但能够发现命题人的命题路径及数学问 题的本质.
点评 在含参数函数不等式恒成立求参数 范围问题中,将不等式两边转化成同构式,根据 同构式构造新函数,利用新函数单调性进一步转 化问题,使得问题得到降维求解,此法虽然有一 定难度,但能够发现命题人的命题路径及数学问 题的本质.
5 虚设零点

 点评 虚设零点体现设而不求思想,是解决导 数问题常用方法,当导数的零点存在但不易求出的 时候,就可以虚设零点,回代到原函数解析式中求 值,确定函数值的符号.
点评 虚设零点体现设而不求思想,是解决导 数问题常用方法,当导数的零点存在但不易求出的 时候,就可以虚设零点,回代到原函数解析式中求 值,确定函数值的符号.
6 数形结合
例 6 设函数 f( x) = ax + cosx,x∈[0,π],设 f(x)≤1 + sinx,求 a 的取值范围.
解析 f(x)≤1 + sinx,即 ax + cosx≤1 + sinx.
可化为 ax - 1≤sinx - cosx.
构造函数 g(x) = ax - 1,h(x) = sinx - cosx,x∈ [0,π],画出函数 g(x),h(x)图象如图 1,g(x)图象 是过(0, - 1)点的直线,h( x) 的图象也过(0, - 1)点,在
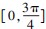
上单调递增,在
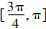
上单调递减, 要使 ax - 1≤sinx - cosx 在[0,π]上恒成立,只需 x ∈[0,π]时 g(x)图象在 h(x)图象下方,由图象知 a ≤

时不等式恒成立,即 a 的范围是
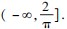
.
点评 数学是研究数量关系和空间形式的科 学,通过挖掘数学式子背后形的特征,以形助数,是 解决数学问题的常用方法.
参考文献:
[1] 张平. 函数与不等式中参数的取值范围[ J]. 中 学数学教学参考,2018(18):30 - 32.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/44614.html
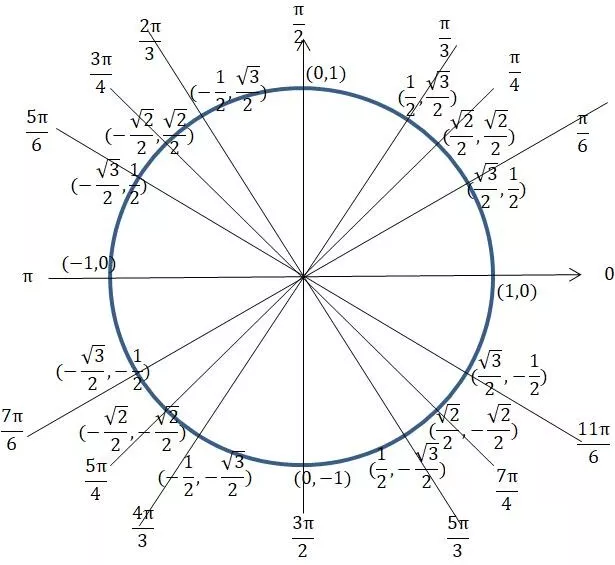











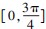 上单调递增,在
上单调递增,在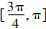 上单调递减, 要使 ax - 1≤sinx - cosx 在[0,π]上恒成立,只需 x ∈[0,π]时 g(x)图象在 h(x)图象下方,由图象知 a ≤
上单调递减, 要使 ax - 1≤sinx - cosx 在[0,π]上恒成立,只需 x ∈[0,π]时 g(x)图象在 h(x)图象下方,由图象知 a ≤  时不等式恒成立,即 a 的范围是
时不等式恒成立,即 a 的范围是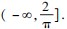 .
.