SCI论文(www.lunwensci.com):
摘要:对典型问题进行多方面探究,就是对问题从不同视角来审视,以不同的切入点探究问题不同的解答方案.经常进行这方面的训练,既能梳理解决这类问题的一般方法,寻求解答此类问题的通性通法,揭示问题的本质和一般规律,又能拓宽学生的知识面,积累解题经验,提高解题效率.
关键词:分式型;二元最值;问题;探究
本文通过对一道二元分式型齐二次条件最值题的探究,使学生学会数学地思考问题,优化数学思维品质.
1试题重现
题目(2021年第31届“希望杯”全国数学邀请赛高二2试第11题)已知a>0,b>0,则


2解法探究

 点评解法1直接在进行代数恒等变换的基础上,利用二元均值不等式求解,其变形过程较为复杂,合理、准确地运用算理、算法进行变形是求解的关键.另外,运用均值不等式求最值时,务必要注意“等号”能否取到,该解法中等号成立的条件,即方程
点评解法1直接在进行代数恒等变换的基础上,利用二元均值不等式求解,其变形过程较为复杂,合理、准确地运用算理、算法进行变形是求解的关键.另外,运用均值不等式求最值时,务必要注意“等号”能否取到,该解法中等号成立的条件,即方程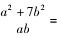 6有解,所以解答是正确的.
6有解,所以解答是正确的.

点评 解法 2 首先进行比值换元和“二层” 换 元,然后进行代数恒等变换,变形出关于“二层” 新 元的均值不等式的结构形式,利用二元均值不等式 求解. 在运用均值不等式求最值时,“等号” 能否取 到是解答的关键.
解法 3 上同解法 2,得
 所以Mu2-8u+36M=0.
所以Mu2-8u+36M=0.
因为u≥

,所以关于u的一元二次方程Mu2-8u+36M=0在[

,+∞)上有实数根.
因为M>0,且二次函数y=Mu2-8u+36M的图象开口向上,
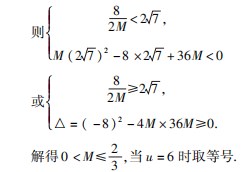
 点评解法4是在解法2进行比值换元和“二层”换元的基础上求导,利用导数研究函数的单调性求解.利用导数求解二元条件最值问题是一种有创意的方法途径.
点评解法4是在解法2进行比值换元和“二层”换元的基础上求导,利用导数研究函数的单调性求解.利用导数求解二元条件最值问题是一种有创意的方法途径.
3试题变式
若将上面赛题中的“系数”7换为5,那么求解的情况是怎样的呢?

 参考文献:
参考文献:
[1]第三十一届”希望杯“全国数学邀请赛高二第2试试题.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/44212.html




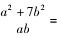 6有解,所以解答是正确的.
6有解,所以解答是正确的.


 ,所以关于u的一元二次方程Mu2-8u+36M=0在[
,所以关于u的一元二次方程Mu2-8u+36M=0在[ ,+∞)上有实数根.
,+∞)上有实数根.