SCI论文(www.lunwensci.com):
摘 要 :复变函数是大学数学的重要组成部分,在培养学生的逻辑思维能力及工程应用中有不 可替代的作用. 科学的课程设计是复变函数教学的重中之重. 本文通过讨论复变函数的课程特色及 目前的教学现状,基于学校提供的雨课堂平台探讨了 BOPPPS 模式在复变函数教学过程中实施的 可行性. 进一步通过案例分析,发现起承转合的 BOPPPS 教学模式不仅利于夯实基础知识,还可以 活跃课堂气氛,带动学生的学习积极性,对课程改革有推动作用.
关键词 :复变函数教学;雨课堂;BOPPPS 教学模式
1 复变函数的教学现状
复变函数中很多定义、性质及定理与实变函数 类似,但其 思 想 和 方 法 上 有 本 质 的 区 别,若 前 期 课程基础不扎实,理论知识薄弱会影响学生对该 课程的学习兴趣;其次复变函数的理论推导及计 算繁琐复杂,传统的“满堂灌”会加重学生的恐惧 感进而打击其积极性;再者应用背景的复杂性及 课时的有限导致教师会忽略背景引入,让学生无 法产生学习动力.
复变函数课程的教学方法已有很多的探讨,如 利用类比教学法将数学分析与复变函数的问题对比 讲授,让学生通过研读、讨论、及撰写论文等形式培 养其自学能力和自主探究的兴趣;通过案例引入发 现探索式教学模式提高对学生数学思维能力的有效 培养作用;通过引入“微课堂”这种具有目标性强、 短小精悍特点的构建主义方法,解决了课时不足,课 堂气氛沉闷等问题. 这些研究方法都是针对教学内 容和教学方法的讨论,没有针对复变函数课程的特点给出完整的课堂教学设计.
2 BOPPPS 模式与雨课堂平台在复变函数教 学应用中的可行性分析
BOPPPS 教学模式是一种以教学目标为导向, 以学生为中心的新型教学模式,,其将教学内容按照 引入、目标、前测、参与式学习、后测及总结六个环节 依次展开,教师以师生互动为核心,通过各类教学手 段来开展教学活动. BOPPPS 教学模式不与传统教 学对立,而是提供了一种理念和框架,教师可根据学 校特点,学科特色及学情等有针对性地改进,进而形 成自己的风格,是一种易学的教学方式. 已经有很多 的学者将这种模式成功运用到教学中,如在线性代数中引入此模式,通过对照实验发现实验班级期末 成绩优秀率高出对照班 14. 2 %;借助学习通给出BOPPPS 在概率论与数理统计中的教学实践过程, 并通过问卷调查的形式反馈出学生对该模式的认可 和喜爱. 这些成功案例对在复变函数课程中实施此 模式有借鉴作用.
复变函数的每章是一个大模块,对应的每节是 一个小模块,章节间各有特点又互有联系,与 BOP- PPS 教学模式适配性很高. 此外复变函数理论性较 强,应用背景复杂,高强度的理论讲述容易让学生产 生脑力疲劳,所以 BOPPPS 模型将课堂内容切割成 15 分钟左右的多个教学小模块,让学生在注意力集 中的阶段高效把握核心知识点,通过起承转合的讲 述,避免内容平铺直叙.
雨课堂是清华大学与学堂在线采用云计算科学 技术共同研发的 一 种新型教学工具,仅需要通过 PowerPoint 和微信将教师端与学生端联系起来,形 成了线上预备与考核,线下互动的混合式教学模 式,其可将 教 学 资 源 轻 松 插 入 幻 灯 片 中,实 现 多 样化教学,通过课前预习与课后作业功能帮助学 生预习和内化知识,课堂上丰富的师生互动形式 带动课堂气氛,下课后通过微信及时反馈课堂情 况,为教师 实 现 动 态 掌 握 学 情 提 供 方 便,且 每 个 环节的打分机制也为平时成绩的合理性提供依 据. 在复变函数课堂中引入这种多样化的教学手 段推动了数学教学改革.
3 基于雨课堂对 BOPPPS 教学模式在课程中 的探讨
目标是 BOPPPS 教学模式的核心,是一节课的 方向引导. 这部分需要教师按照教学大纲制定. 在课 堂上教师需言简意赅的阐明本堂课的学习任务及学 习后应掌握什么,而不是将教学目标直接展示.
导入是为了吸引学生注意力,引导其对预讲内 容有强烈的好奇心和学习兴趣,这部分对教师的专 业素养及数学文化素养有很高的要求,教师需要把 握所讲章节在整个教材中的地位和重要性,还需教 师对基础理论的背景和应用有深入挖掘. 导入的方 式应随章节及内容灵活处理,切勿生搬硬套,无法引 起学生共鸣. 这部分教师可借助雨课堂的资料视频 及技术手段,从不同角度去开展.
前测是对学生的一次摸底考试,雨课堂丰富的 测试功能可协助教师完成此教学环节. 复变函数中 对定理的灵活运用需要学生对其条件的精准掌握, 前测可以让教师了解学生的基础掌握情况,进而调整接下来的参与式互动环节,同时对学生的课下复 习起到督促作用.
师生参与式学习是课堂教学的核心,这部分教 师可以根据班级学情和自身经验,以学生为中心,合 理运用雨课堂资源进行展开,增强参与式的师生交 互学习效果. 后测是对参与式学习的检验和评估,教 师应设置合理的能体现本节课目标的习题与互动进 行评估,进而适时调整后续总结与模块引入. 最后教 师需要带领学生进行核心知识点的总结,这既是一 种复习,也是一种知识内化,不可或缺. 同时教师应 积极参与 BOPPPS 教学模式的研讨会等,通过与同 行新老教师积极交流合作,分享经验与体会,加深对 教学模式的强化认识.
BOPPPS 教学模式需要学生对课程的基础知识 如数学分析掌握较好,故教师应对班级学情有所了 解,备课时应充分考虑对基础知识的回顾与总结. 而 复变函数课程课时一般都比较紧张,课堂上的互动 会占用很长时间,所以建议教师借助雨课堂布置课 前预习,通过添加习题、视频及语音等材料内容向学 生手机端推送,并通过雨课堂的观看时长,是否观看 课件等记分机制给学生预习打分,督促学生进行预 习,让学生养成主动学习的习惯.
4 复变函数课堂教学设计策略
本文以复变函数中第五章第 1 节内容“解析函 数的洛朗展式”为例,进一步结合雨课堂给出 BOP- PPS 教学模式下复变函数的课堂设计策略. 这一节 内容一个课时可划分成两个教学模块,接下来对第 一个教学模块进行教学展示.
4. 1 导入
通过给出函数f(z ) =

引导学生讨论其在
整个复平面上的解析性;其次通过f(z ) = 在 z=0 的幂级数展开式及展开区域 z < 1,对比解析区 域及展开区域引导学生发现此函数仅因为一个奇点 却使得函数只能在小区域 z < 1 展开成幂级数,提 问学生对于 z > 1 这个区域解析函数能展开成级 数形式吗?
在 z=0 的幂级数展开式及展开区域 z < 1,对比解析区 域及展开区域引导学生发现此函数仅因为一个奇点 却使得函数只能在小区域 z < 1 展开成幂级数,提 问学生对于 z > 1 这个区域解析函数能展开成级 数形式吗?
4. 2 目标
通过幻灯片展示 :在本节课后学生应能掌握函 数可展成双边幂级数的条件,并能熟练给出特定区 域的展式,为留数的计算打好基础.
4. 3 前测
本模块以幂级数的相关理论及柯西积分公式为基础,利用雨课堂的课堂互动功能,制作幻灯片测试题.
判断题 :若函数f(z )在 z0 处解析,则它在该点 的某个邻域内可展开为幂级数(√ ) .
单 项 选 择 题 : 设 幂 级 数
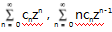
和

的收敛半径分别为 R1,R2,R3,则 R1,R2,
R3 之间的关系为( ) .
A. R1 < R2 < R3 B. R1 =R2 =R3
C. R1 > R2 > R3 D. R1 < R2 =R3
利用随机点名功能或者学生主动参与方式回答 柯西积分公式的内容,根据客观题的作答情况灵活 调整参与式学习部分,并将得分记为平时分的一部 分,督促学生参与进课堂中来.
4. 4 参与式学习
因为本节概念及定理较多,故以学生为主体,采 用 PBL(基于问题的学习)方法进行.
问题 1 :什么是双边幂级数? 与幂级数有什么 区别?
问题 2 :教师通过课件展示定理 5. 1,提问学生 此定理如何证明?
问题 3 : 洛 朗 系 数 有 微 分 形 式 吗? 即 cn =
 是否成立? a 一定是f(z )的奇点吗?
是否成立? a 一定是f(z )的奇点吗?
4. 5 后测
通过计算例题 :讨论f(z ) =在区域 z > 1处是否可以洛朗展开,了解函数洛朗展开的方法.
学生通过例题总结出直接利用定理计算洛朗系 数 cn 较麻烦,指导学生借助幂级数的展开给出其洛 朗展式,由此启发学生依据洛朗展式的惟一性,幂级 数的间接展开方法也可以用到计算洛朗展式中来.
至此这一模块的教学环节完成,这是笔者对自 己复变函数教学活动的一种展示,在期末复习阶段通过问卷调查的形式反馈出学生们对此模式的支 持,同时也得到了很多有益建议,帮助笔者进一步改 进和优化各个环节.
随着信息化时代互联网的快速发展,传统的高 等教育模式急需转变,高校的教育教学改革势在必 行. 本文通过复变课程的课程特点及教学问题,分析 了当下被广泛讨论的 BOPPPS 教学模式在复变函数 课程中实施的可行性. 模块化的 BOPPPS 教学模式 以学生 为 中 心,重 视 学 生 的 课 堂 参 与 度 与 主 动 性,有利于 复 变 函 数 的 教 学 过 程 的 开 展. 其 次 将 教学工具嵌入 PowerPoint 与微信这两个熟悉的软 件中,让教 师 与 学 生 群 体 均 易 于 操 作,不 介 入 其 他软件,对 教 育 教 学 活 动 有 很 好 的 借 鉴 作 用. 最 后对于此模式的选择并不是 一 劳永逸的,在实际 的教学活动中,需要教师根据所教授课程的特点 灵活调整,切勿生搬硬套.
参考文献 :
[ 1 ] 秦宝侠. 基于能力培养的复变函数教学改革研 究 [J ] . 齐鲁师范学院学报,2018,33(6 ) :5 .
[2 ] 王胜军. 基于复数与复变函数的探究式教学模 式探讨[J ] . 青海师范大学学报( 自然科学版), 2020,36 (04 ) :67 - 69 .
[3 ] 王洪涛,仝卫卫. 让“微课程”走进课堂—谈 《复变函数与积分变换》教学改革 [ J ] . 教育教 学论坛,2018(44) :2 .
[4 ] 曹丹平,印兴耀. 加拿大 BOPPPS 教学模式及其 对高等教育改革的启示 [ J ] . 实验室研究与探 索,2016,35 (2 ) :6 .
[5 ] 王华丽,冯倩倩. BOPPPS 教学模式在线性代数 教学中的应用及效果评价 [J ] . 黑龙江科学, 2021,12 ( 1 ) :2 .
[6 ] 吕宁. 基于超星学习通 BOPPPS 模型的概率论 与数理统计教学改革实践[J ] . 科技视界,2021 ( 14 ) :5 .
[7 ] 邓亮. 基于“雨课堂”混合式教学模式设计与实 践[J ] . 中国人民公安大学学报( 自然科学版), 2017,23 (2 ) :4 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/43595.html
 引导学生讨论其在整个复平面上的解析性;其次通过f(z ) =
引导学生讨论其在整个复平面上的解析性;其次通过f(z ) = 在 z=0 的幂级数展开式及展开区域 z < 1,对比解析区 域及展开区域引导学生发现此函数仅因为一个奇点 却使得函数只能在小区域 z < 1 展开成幂级数,提 问学生对于 z > 1 这个区域解析函数能展开成级 数形式吗?
在 z=0 的幂级数展开式及展开区域 z < 1,对比解析区 域及展开区域引导学生发现此函数仅因为一个奇点 却使得函数只能在小区域 z < 1 展开成幂级数,提 问学生对于 z > 1 这个区域解析函数能展开成级 数形式吗?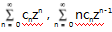 和
和  的收敛半径分别为 R1,R2,R3,则 R1,R2,R3 之间的关系为( ) .
的收敛半径分别为 R1,R2,R3,则 R1,R2,R3 之间的关系为( ) .
 是否成立? a 一定是f(z )的奇点吗?
是否成立? a 一定是f(z )的奇点吗?