SCI论文(www.lunwensci.com):
摘要:直观想象核心素养是学习者理解数学问题和探索数学结论的重要基础,学习者形成直观想象素养,需要依托空间形式尤其是几何图形来理解抽象的事物和过程。知识可视化可以将抽象的数学问题、过程转化为形象具体的呈现。本文以GeoGebra技术为平台,构建直观的图解手段或动态的几何图形,以知识可视化的角度来帮助学习者分析和理解数学问题,从而促进学习者直观想象素养的发展,最终实现数学的学科素养。
关键词:动态几何;知识可视化;直观想象素养;GeoGebra软件
本文引用格式:于金萍,等.基于知识可视化视角的直观想象素养培育研究[J].教育现代化,2019,6(79):216-219.
教育部发布的“《教育部关于全面深化课程改革,落实立德树人根本任务的意见》要求各级各类学校把发展核心素养和提升学业质量落实到所有学科的教学中,说明了学科核心素养的重要性。直观想象素养包含几何直观和空间想象这两个关键词,几何直观指的是借助于比较直观的几何图形来解决数学问题,空间想象指对立体图形的空间形式进行认知和分析的思维能力。[1]中学阶段学生对几何的学习由平面逐渐转为立体,这就要求学生要有一定的空间想象能力。而这一阶段的学生数学基础较为薄弱,数学素养不高,传统的黑板或PPT课件只能给学生创设对应的情境,无法展示数学中动的过程。计算机不仅是代数和微积分教学的重要辅助工具,也是使二维或三维图形进行知识可视化的重要方式之一。“《教育信息化2.0行动计划》指出,未来教育信息化将作为主要力量引领教育向着现代化迈进。研究表明,使用设计良好的知识可视化工具,结合局部探究的教学形式可以有效地提高学生的思维,[2]知识可视化的教学应用对学生成绩、认知技能以及学习情感产生积极影响。[3]
利用丰富多彩的知识可视化手段可以将抽象复杂的数学问题变得简单直观,可以将静止的图形运动起来,便于理解。[4]借助于可视化技术,对生活中的问题进行模拟并抽象为数学问题,是科学教育的关键。
一 知识可视化的框架与工具
可视化是指充分利用人们对图形快速识别的能力,将数据、信息和知识转化为形象具体的视觉表征形式,以便于信息的传达和理解。[5]M.J Eppler和R.A Burkard认为:知识可视化是一种新的研究领域,是以计算可视化、数据可视化、信息可视化为基础进一步发展起来的。其目的主要是应用视觉表征手段,提高两人或多人之间的知识创造和传递,以及传输观念、经验、预测价值观和态度等。[6]
(一)知识可视化的框架
关于知识可视化的框架,不同学者都提出自己了的观点,这里介绍一种典型的框架。如图1所示:
该框架了阐明了知识可视化在实践过程中要认真研究的三个“关键的问题”,即:什么类型的知识可以可视化?不同的文献对知识类型分类各不相同,因此无法提供一个标准的与此相对应的知识分类法。对这些知识进行可视化的原因?也就是可视化的目的,包括:进行知识的共享或传播、创造、学习、或把习得的经验制成文档供别人使用等。[7]以及如何进行可视化?包括概念图表、视觉隐喻、知识动画等。此框架中关于知识的类型、可视化的目的以及可视化形式的关系只是一个示意,不是一一对应的,应用时仍需研究者具体分析。[8]
(二)知识可视化的工具
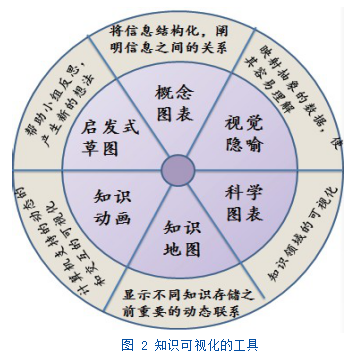
R.A.伯卡德和M.J.埃普拉(2004),将知识可视化的工具分为六种类型如图2:概念图表、视觉隐喻、科学图表、知识地图、知识动画、启发式草图。
本文主要研究借助于动态的,交互的可视化软件——GeoGebra呈现出传达知识的图解手段以及动态的几何环境,帮助学生理解抽象的事物或过程,在图形的变换中提高对动态几何结构的理解能力,从而促进学生直观想象素养的提高。
二直观想象素养及其结构模型
(一)直观想象素养
直观想象素养是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养。它的三个水平划分为:
水平一:看图想式
能理解图形表达的意思并在具体的情境中把实物的几何图形抽象出来,并根据图形把实物想象出来。
水平二:看式构图
能在相关联的情境中想象出几何图形,并把相对应的几何图形构建出来,并借助于几何图形发现问题。
水平三:综合应用
能借助图形对数学各部分之间的联系进行综合理解并分析,在科学的情境中建立数与形的联系,通过构建直观模型来探索解决问题的思路。
水平一可以概括为“看图想式”,即看到图形就能想到与之相对应的数学式子。水平二可以概括为“看式构图”,即由数学式子能构造出一个图形来解决实际问题,这就增加了难度,属于逆向思维。水平三可以概括为“联系应用”,既可以是数学各部分知识点之间的联系,也可以是跨学科建立直观模型,属于通过创新知识来解决问题。[10]
(二)直观想象素养的结构模型
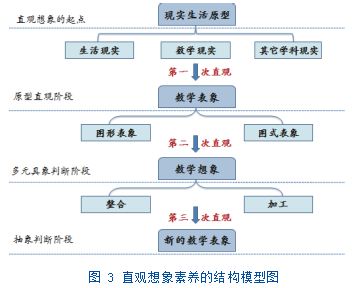
在对直观想象素养进行分析和研究的基础上,已有学者将直观想象素养的形成过程构建出来,如图3所示:共划分为四个等级,四个等级之间分别构成三次直观。第一级为直观想象素养形成的起点,即现实生活原型。这里的原型包与现实生活有关的生活现实,学习者已经习得的数学现实,以及其他学科的现实。第二级是基于以上原型产生的数学表象。第三级为数学想象,是基于原型直观形成的,学习者开始对想象进行加工和整合。第四级为新的数学表象,此时学习者保留之前想象的特征,处于抽象全称判断阶段。三次直观体现了化抽象为具体的过程。[11]
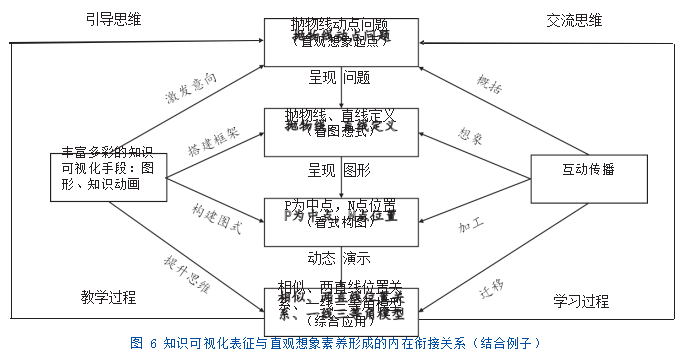
(三)知识可视化表征与直观想象素养形成的内在衔接关系
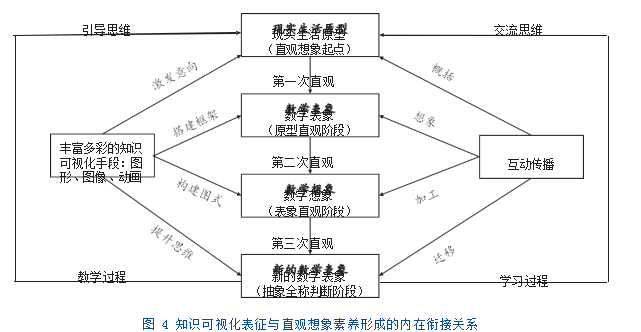
学习者不是被动接受者和被灌输的对象,而是知识的主动建构者。“思考”与“联系”在学习者主动建构知识的过程中起着至关重要的作用。因此本研究是在教学过程中借助于丰富多彩的知识可视化手段如图形、图像、动画等,激发学习意向,帮助学习者主动对问题进行概括、想象搭建新的知识框架,学习者头脑中的想象经过加工后形成新的图示,并将知识迁移到相关联的情境中,将知识牢固的的储存在长时记忆中,达到提升思维的目的,从而达到直观想象的三个水平。[12]
三直观想象素养的体现——抛物线动点问题
二次函数是一种常见的函数,应用十分广泛。它是客观地反映变量之间的数量关系和变化规律的重要数学模型。初中教材已经对二次函数进行了介绍,但初中学生基础薄弱,数学素养不高,所以这部分内容多数是机械式的重复讲授与练习。而高中教材就对函数部分进行了比较系统的介绍,需要学习者能灵活运用。因此,函数问题就成了培养直观想象素养的最佳载体。下面以抛物线问题为例运用知识可视化手段来体现直观想象素养三个水平的教学。

(1)求直线AB的解析式;
(2)若点P是线段MN的中点,那么此时点N的坐标为;
(3)如果以N、B、P、为顶点的三角形与AP相似,求此时点M的坐标。
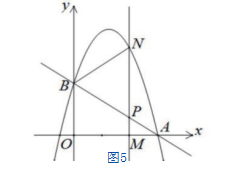
由抛物线的动点问题引出的三个不同的问题分别对应直观想象素养的三个水平,如图6所示,问题(1)比较简单,通过观察图形即可解决,即能看图想式,属于水平一的直观想象。问题(2)利用知识可视化手段让图形动起来,学习者通过观察,将自己的想象进一步加工最终解决问题,属于水平二的直观想象。问题(3)将抛物线的动点问题迁移到相似三角形问题上,通过对图形动态的演示帮助学习者综合的考虑问题,提升学生的思维,属于水平三的直观想象。整个过程采用小组合作交流与借助GeoGebra技术局部探究的形式,教学过程中教师要注意引导学习者的思维,学习者在学习过程中也会相互交流思维。
水平一:看图想式
问题(1)比较简单,用代入法即可解决,故属于水平一的直观想象。
水平二:看式构图
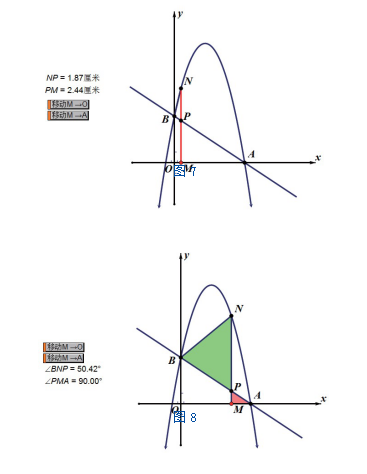
含有变量的问题比较抽象,学生在想象变化的量的问题上比较困难,黑板虽然能画出变化后的最终图形,但是无发展是变化的过程。针对问题(2),利用GeoGebra技术,如图7所示能帮助教师展示点M运动的整个过程,让学习者自主探索出与所求问题最符合的情况,从而得出合理的猜想并解决问题。而问题(2)综合性较强,需要学习者想象相应的几何图形(如图1),构建新的图示,并根据图形解决问题,故属于水平二的直观想象。
水平三:综合运用
问题(3)需要学习者在点动的情况下考虑图形的相似情况,利用GeoGebra技术让动点真正的动起来,如图8所示把两个相似的三角形设置不同的颜色,度量出对应角的度数,再点移动过程中如果对应角的度数相等则为相似三角形。问题(3)在抛物线的情境下涉及了相似三角形、两直线的位置关系以及一线三等角模型,综合运用数学知识间的相互联系,通过动画演示能充分的训练学习者的想象力,提升学习者的思维,属于水平三的直观想象。
四 结语
知识可视化手段的运用对直观想象素养的培育具有重要作用,对改变学习者的思维方式以及提升他们的思维具有重要影响。基于GeoGebra技术平台,将复杂与抽象的数学问题转化为简单直观的呈现,有利于学习者进行数学化的思考和想象,从而提升学习者的直观想象素养,最终实现数学的学科素养。
参考文献
[1]朱立明,胡洪强,马云鹏.数学核心素养的理解与生成路径—以高中数学课程为例[J].数学教育学报,2018,27(1):42-46
[2]伍国华,李克东.知识可视化教学应用的元分析研究[J].电化教育研究,2011(12):84-90.
[3]Hagar Gal&LioraLinchevski.(2010).To see or not to see:analyzing difficulties in geometryfrom the perspective of visual perception.Educationudy Study in Mathematics.
[4]王雪,王志军.多媒体课件中的信息加工整合策略的研究与设计——以初中数学课件“二次函数”为例[J].电化教育研究,2015,36(04):103-107.
[5]赵慧臣.知识可视化视觉表征的分析框架[J].开放教育研究,2010,16(05):51-58.
[6]Hoffler,T.N.,&Leutner,D.(2007).Instructional animation vers us static pictures:a m eta-analys is.L earning and Instruction,17(6):722-738.
[7]刘超.近十年国外知识可视化研究发展述评[J].上海教育科研,2012(09):32-36.
[8]赵国庆,黄荣怀,陆志坚.知识可视化的理论与方法[J].开放教育研究,2005(01):23-27.
[9]Gyllenpalm,J.,&Wickman,P.-O.(2011).The uses of the term hypothesis and the inquiry emphasisconflation in science teacher education.International Journal of Science Education,33(14):1993–2015.
[10]王华,沈金兴.基于直观想象“3个水平划分”的教学——以“几何法”解向量问题为例[J].中学教研(数学),2018(11):1-5.
[11]吴立宝,刘哲雨,康玥.直观想象素养的内涵与结构探究[J].现代基础教育研究,2018,31(03):109-113.
[12]Betrancourt,M.(2005).The animation and interactivity principles in multimedia learning.In R.E.Mayer(Ed.),The Cambridge handbook of multimedia learning(pp.287–296).New York:Cambridge universityPress.
[13]赵国庆,黄荣怀,陆志坚.知识可视化的理论与方法[J].开放教育研究,2005(01):23-27.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/29679.html