SCI论文(www.lunwensci.com):
摘 要:数学新课标强调信息技术与数学教学的融合,发挥技术优势,优化数学课堂教学,培养学生数学核心素养。GeoGebra 作为信息技术辅助教学的软件平台,将其与几何教学有机融合,有助于学生发展空间视觉能力、几何推理能力和高水平的思维能力。本文讨论了动态几何软件 GeoGebra 的特点和功能,构造了 GeoGebra 软件的设计模型,用 GeoGebra 软件进行几何教学实验研究,对实验组与对照组进行前测与后测,使用 SPSS 软件进行数据统计分析。分析结果表明,使用 GeoGebra 进行几何教学的学生的表现与传统教学之间存在显著性差异,结合实验结果与几何教学案例,阐明了 GeoGebra 软件与几何教学整合的优势。
关键词:GeoGebra;GeoGebra 设计模型;SPSS 软件;几何教学
本文引用格式:郭欣阁,吴华 . 基于动态几何软件GeoGebra 的高中几何教学研究[J]. 教育现代化,2021,8(32):12-16.
High School geometry Teaching Research Based on dynamic geometry Software geogebra
GUO Xinge,WU hua
(School of Mathematics, Liaoning normal University, Dalian Liaoning)
Abstract: The new mathematics curriculum standard emphasizes the integration of information technology and mathematics teaching, makes use of technical advantages, optimizes mathematics classroom teaching, and cultivates students’ core literacy in mathematics.GeoGebra, as a software platform for information technology-assisted teaching, integrates it with geometry teaching, which helps students develop spatial vision, geometric reasoning and high-level thinking skills.This article discusses the characteristics and functions of the dynamic geometry software GeoGebra, constructs the design model of GeoGebra software, uses GeoGebra software to conduct geometric teaching experimental research, conducts pre-test and post-test on the experimental group and the control group, and uses SPSS software for statistical analysis of data.The analysis results show that there is a significant difference between the performance of the students who use GeoGebra for geometry teaching and traditional teaching. Combining the experimental results and geometry teaching cases, it clarifies the advantages of the integration of GeoGebra software and geometry teaching.
Keywords: GeoGebra; GeoGebra design model; SPSS software; geometry teaching
一 引言
几何学是学生发展思维过程的重要组成部分。通过学习几何,学生将学习几何形状和结构,并分析它们的特点和关系。在几何的教学中 , 要重视文字语言、图形语言、符号语言之间的相互转化,引导学生及时地将文字条件转化为图形条件和符号表示,在图形中进行条件和结论的标识,更直观地帮助学生进行条件的分析和结论的证明 [1]。随着人类社会和科学技术的不断进步,数学基础教育的内容绝不能墨守成规、一成不变,而应该与时俱进、不断更新, 努力体现现代化的要求 [2]。
可视化辅助在几何学习中起着重要的作用。使用可视化的数据可以使学生更容易地看到用思维很难看到的数据,这样学生可以观察模拟和计算。因此, 在学习数学的过程中,有必要使用可视化的数学软件进行创新。随着科学技术的发展,计算机软件在数学教学中的可用性问题已经得到了广泛的研究和开发 [3]。GeoGebra 就是其中的一个软件产品,可以用来辅助高中几何教学。在传统课堂教学中,教师通过讲解和手绘图形,很难准确快速地画出空间几何与曲线等图形,且缺乏动态性与直观性,学生容易失去学习兴趣。使用 GeoGebra 软件进行几何教学,可以做出生动形象的图形,且可以提高作图效率。本文将结合 GeoGebra 软件的特点列举其在几何教学中的几点优势。
二 GeoGebra 软件概述
(一) GeoGebra 软件特点及功能
GeoGebra 是一款集几何、代数、微积分、概率统计等功能于一体的动态几何软件。该软件是一款完全免费的,开源的交互式动态几何软件,由美国佛罗里达州亚特兰大大学数学系教授 Markus hohenwarter 及其团队共同开发,可实现在从小学到大学的不同阶段数学教学中应用。GeoGebra 是由“Geometry”( 几何) 和“Algebra”( 代数) 组成的新生词汇,被很多人简称为“GGB”。此软件发展至 今,一直走国际化的开源发展之路,目前不仅可支 持 Windows、Mac、Android、iOS 等不同平台运行, 更有 56 种语言翻译的版本,并且荣获多种教育类软件奖项 [4]。GeoGebra 软件拥有如下的功能:
(1)快速作图功能
一款能被广泛应用的教学软件,简便易用是基础。GeoGebra 软件界面简洁丰富,GeoGebra 拥有丰富的工具。在 GeoGebra 的工具栏中,使用者既可以通过使用简单的点线工具进行尺规作图,又可以通过平面几何工具、立体几何工具等丰富的工具快速做出常用的图形。
(2)数形结合功能
GeoGebra 软件通过绘图区和代数区实现了几何与代数的同步变化 [5]。在绘图区建立的所有对象, 都对应在代数区中显示数值、描述或定义,当对象在绘图区发生改变时,代数区的数值也对应改变, 实现了真正的动态同步变化。
(3)脚本指令功能
GeoGebra 软件拥有一个丰富的脚本指令库,并支持 68 种语言的输入,使用者通过“输入框”输入脚本指令,可以实现几何、代数、函数与微积分、概率、统计等对象的快速建构。在触发脚本之后,将逐个执行每个命令。
(二) GeoGebra 软件设计模型
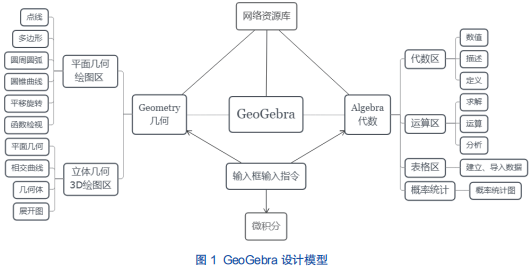
GeoGebra 结合了其他动态几何软件的易用性与代数软件的灵活性。该软件的系统设计模型图如图 1 所示,其基本理念是将几何、代数和微积分结合在一起,并通过代数区、绘图区、3D 绘图区、运算区、表格区等不同区域实现不同的功能,并且在不同的区域,对应不同的工具,例如:在绘图区,可以通过圆弧工具在平面直角坐标系中绘制圆弧、圆形、扇形等平面几何图形;在 3D 绘图区,则可以通过几何体工具直接在三维坐标系中绘制球体、正方体等几何图形。
三 实验研究及结果
(一) 研究方法
本研究采用实验研究,在盘山县高级中学选取高二年级两个班级分别作为实验组和对照组做对比试验,共有 91 名学生参与了这项研究,其中实验组总人数为 44 人,对照组为 47 人。在实验组实行基本研究采用实验研究,在盘山县高级中学选取于 GeoGebra 软件的几何教学,在对照组实行传统方式开展教学。为了保证科学性,先后进行实验前成绩测试(前测)和实验后成绩测试(后测),并使用 SPSS 软件对成绩进行统计分析。
(二) 实验前成绩测试分析
为了获取学生在实验前的学习情况,将学生的数学入学成绩收集整理,此次实验选择独立样本 t 检验方案进行实验结果数据分析,分析结果如表 1 所示。
对于两个组的入学成绩,实验组与对照组的平均成绩分别为 121.82 分和 119.81 分。在独立样本 t 检验中, 显著性 p=0.257 > 0.05, 所以表明两总体方差齐性,因此选用方差相等的检验结果。t = 0.709, 显著性(双尾)p=0.480 > 0.05,从这个方面可以看出两组入学成绩不存在显著差异,因此可以将实验组与对照组作为平行班进行实验研究。
(三) 实验后成绩测试分析
在进行了一个月的实验后,对两个组的月考成绩进行数据分析,将学生的月考数学成绩收集整理, 此次实验同样选择独立样本 t 检验方案进行结果数据分析,分析结果如表 2 所示。

实验组和对照组的测试平均成绩分别为 116.25 分 和 110.74 分 。 在 独 立 样 本 t 检 验 中 , 显 著 性p=0.394 > 0.05,所以表明两总体方差齐性,因此选用方差相等的检验结果。t = 2.274,显著性(双尾) p=0.025 < 0.05,从这个方面可以得使用 GeoGebra 软件进行几何教学与使用传统课堂相比学生成绩存在显著性差异。
四 GeoGebra 软件与几何教学
(一) 几何教学的特点
对学生来说,空间与图形是帮助他们更好地生存并促进他们发展的重要基础 [6]。在几何学习中, 学生将学习几何的形状和结构,并分析它们的特点和关系,既可以发展思维过程、激活创造力、发展分析问题和解决问题的能力,又有助于其他数学知识的学习。几何的学习也有助于建立空间能力、几何推理能力和强化数学思维。几何在学生直观想象数学核心素养发展中发挥许多作用,为学生发展空间视觉能力和几何推理能力提供了广阔的机会,从而获得高水平的思维能力。
(二) GeoGebra 软件在几何教学中的优势
许多研究表明,GeoGebra 可以鼓励学生在课堂上进行发现和实验。GeoGebra 特别匹配几何材料, 因为它不仅提供了在屏幕上转换对象的功能,也可以让用户可以方便地绘制几何图形,精确地测量距离、角度和宽度,还提供了点击拖动功能,让学生有机会破解或构建需要可见性的主题中的几何图形,比如旋转子部分中的几何变换 [7]。通过实验研究可以看出在几何教学中使用 GeoGebra 软件,可以有效地提高学生的学习成绩,笔者对比传统教学,总结GeoGebra 软件在几何教学中有以下几点优势:
(1)可视化几何概念
在几何教学过程中,主要的研究对象为空间与图形。在传统课堂教学中,教师只能通过描述、手绘或模型展示的方式教授学生相关概念,因此有很多局限性。使用 GeoGebra 软件进行几何教学,教师可通过软件中丰富的工具及指令,展示任意图形, 使学生进行直观思考,将抽象的几何概念可视化。使用 GeoGebra 软件不仅可以提高学生的学习兴趣, 还有利于学生对知识的了解。
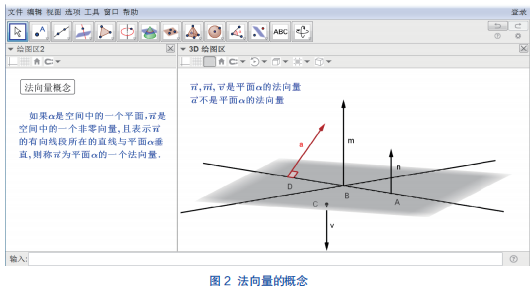
例如,法向量是高中几何学习中重要的概念之一,正确理解法向量的概念,对学好其他几何知识非常重要。法向量有两个基本要素:(1) 非零向量;(2) 一个平面有无数个法向量。在 GeoGebra 软件的 3D 绘图区中,利用 GeoGebra 软件中的“垂线”工具, 先后选出垂足 A、B、C 做三条垂线,并分别在三条垂线上选择三个点,并用“向量”工具做出平面的三个法向量,可通过移动三点让学生直观感受一个平面的多个法向量。如图 2,使用“直线”工具建构直线 AB,在直线 AB 上选取一点 D,过点 D 及平面外一动点 E 做与直线 AB 垂直的向量 a ,此向量不是
平面的法向量,但学生可通过移动点,使 a 变成平面的法向量,使学生直观感受,理解法向量的概念。
教师通过 GeoGebra 制作积件来进行课堂演示, 让复杂抽象的几何学习变得直观、生动,有效提高学生学习几何的兴趣,让学生建立空间几何能力、几何思维水平、强化数学思维。
(2)利用 GeoGebra 软件验证或演示几何命题
几何的学习具有一定的演绎推理体系,体系之间的知识联系密切,形成一个知识网络。在传统课堂教学中,教师没有合适的工具,来通过几何直观验证或演示几何定理和性质。教师可以借助GeoGebra 软件强大的动态展示功能,将静态的图形动态化展示,并结合测量、计算等工具可以帮助教师实现直观化地演示几何定理和几何性质。
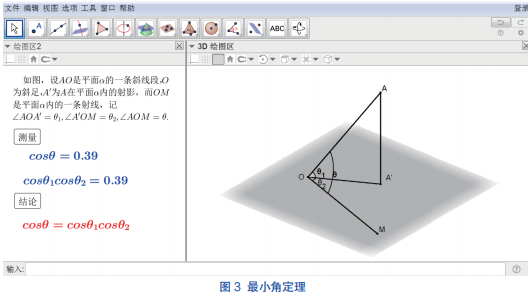
例如,教师可以利用 GeoGebra 软件验证最小角定理。在 GeoGebra 软件 3D 绘图区使用“线段”工具,依次选择平面上一点 O 和平面外一点 A;然后选择“垂线”工具,依次选择点 A 和平面建构垂线交平面于点 B;在平面内构件任意一点 M,并选择“线段”工具,连接 OB 和 OM;用角度工具分别构造∠ AOB、∠ BOM、∠ AOM 为 θ1、θ2、θ ;最后通过“文本”工具,分别计算cos θ 和 cos θ1 cos θ2的值。用“移动”工具变换不同的角度,两组值恒相等,通过GeoGebra 的功能可以实现在变化的过程中,找到不变的关系。即可验证定理的成立。
(3)利用 GeoGebra 发展学生的直观想象学科素养
直观想象是发现和提出问题、分析和解决问题的重要手段,是探索和形成论证思路、进行数学推理、建构抽象结构的思维基础 [8]。教师使用 GeoGebra 来辅助几何教学,在教学过程中还可以借助 GeoGebra 的功能将抽象的几何知识变成具体的几何知识,从而有效提高教学效果。GeoGebra 软件中有个独特的工具一“滑动条”,教师可以利用滑动条控制数量、角度、参数的变化,通过移动滑动条,可以使几何图形实现旋转、平移、翻折等变化,同时代数区所对应的数量关系也会实时变化。一系列的操作可实现从量变引起形变,再由形变带动量变。
在高中数学学习中融入了大量的立体几何知识,如:空间中的平行关系、空间中的垂直关系、多面体、球体等。当学生从二维平面上升到三维空间的学习时,学生的空间想象能力往往会成为一种阻碍,我们可以借助 GeoGebra 软件来克服阻碍。例如,在学习“平面的基本事实与推论”时,可以利用 GeoGebra 软件的 3D 绘图区, 首先用描点工具建立点 A,再分别创建滑动条 α、β,设置滑动条属性为角度,选择旋转工具将点 A 分别围绕 x 轴与y 轴旋转 α 和 β 角度到点 A'',其次分别创建直线Á''C 和直线外点 B,最后使用“平面”工具,通过直线与直线外一点,感受平面的特点,并通过滑动条的变化,直观感受变化的性质,加深理解。
五 结 语
如今,在信息技术飞速发展的环境下,对比传统的课堂教学,教师使用 GeoGebra 软件进行几何教学, 可以提高学生进行活动或获得答案的速度,以及理解概念的速度,帮助他们克服几何教学领域的一些障碍。但同时,教师要有必要的技能来整合 GeoGebra 软件作为教学的一部分,这就对教师提出了新的要求与挑战。
参考文献
[1]王轲 . 立体几何教学中培养学生逻辑推理素养的探究 [J]. 中学数学研究 ( 华南师范大学版 ),2020(16):19-21.
[2]徐岳灿 . 高中数学立体几何教学关键问题与对策 [J]. 上海课程教学究 ,2018(04):39-45.
[3]Akkaya A,Tatar E,Kağızmanlı T B.Using dynamic software in teaching of the symmetry in analytic geometry:The cas e of Geogebra[J ].P rocedia-Social and Behavioral Sciences,2011,15:2540-2544.
[4]张明 . 动态数学软件 GeoGebra 的发展历史和功能特点 [J]. 课程教育研究 ,2015(21):216.
[5]项俊 .GeoGebra 软件在高中数学教学中的应用探究 [J]. 上海中学数学 ,2019(04):25-27.
[6]许志峰 . 对中学几何教学特点的认识及其思考 [J]. 成才之路 ,2010(24):44-45.
[7]Bernard M, Setiawan W. Development of Geometry Analysis Using Geogebra Scripting in terms of Student Cognitive Capabilities[C]. Journal of Physics: Conference Series. 2020, 1521: 032103.
[8]中华人民共和国教育部 . 普通高中数学课程标准 [M]. 北京 : 人民教育出版社 ,2017:6.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/32642.html