SCI论文(www.lunwensci.com):
摘要:文章利用spss软件对某高校的12个二级学院,223门课程,674个相关班级的试卷质量问卷调查进行回归分析,从试卷的调查问卷中的8个相关因素中得出对学生成绩优秀率的影响因素以及其线性模型公式,为之后教师的授课及试卷的制作提供了相对明了且良好的改良及提高方向。
关键词:spss软件;试卷调查表;优秀率;影响因素;试卷制作
本文引用格式:马文广等.基于SPSS软件分析学生成绩优秀率的影响因素[J].教育现代化,2019,6(31):184-186.
Analyzing the Influencing Factors of Student Performance Ratio Based on SPSS Software
MA Wen-guang1,MA Shang-quan2
(1.Graduate Department of North China Institute of Technology Beijing,China;2.North China Institute of Technology Personnel Office,Beijing,China)
Abstract:this paper uses SPSS software to analyze the quality questionnaire of 12 secondary colleges,223 courses and 674 related classes.From the eight relevant factors in the questionnaire of the test paper,the influence factors on the student’s performance rate and its linear model formula are obtained,which provides relatively clear and good improvement and improvement direction for the teacher’s teaching and the production of the test paper.
Keywords:SPSS software;(a)A test questionnaire;Excellent rate;Impact factors;Paper production
现阶段我国高校对于大学生所学课程知识的掌握理解程度仍然主要以考试成绩的高低来体现[1],代课教师需要通过试卷分析来检查教学效果,鉴定教学质量[2],还能调整和改进教学工作,激发学生学习行为,通过学生成绩的分布来对试卷质量进行分析评价,并逐渐积累好的题目,完成建立题库的任务,逐步推进当前教学评估工作使之走上一个新台阶确保学生成绩分布基本呈正态分布[3]。这对教学质量和学生质量的提高都具有重要的现实意义。
一 总体分析
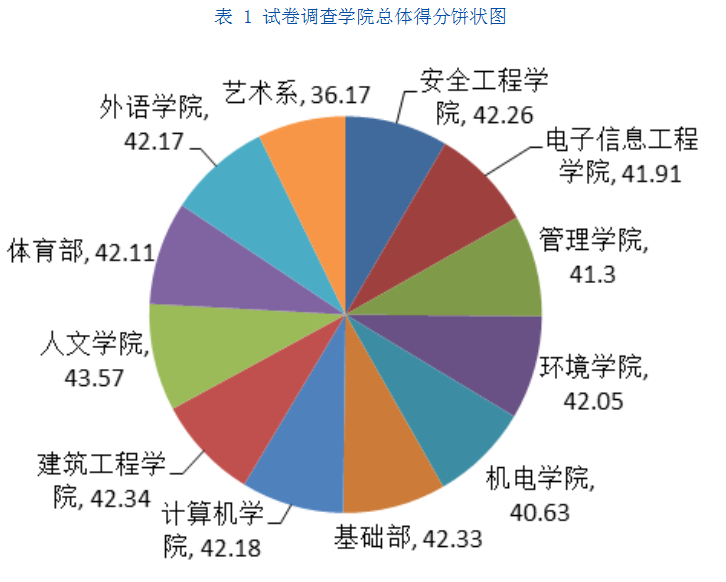
现以某高校2017~2018第二学年试卷质量评估问卷来分析学生优秀率和试卷各项问题的相关性。其中包括我校12个二级学院,223门课程,674个相关班级的试卷。
试卷由学校督导组专家对试卷进行打分评估,其中因素包括:是否符合专业教学的教学大纲基本要求,有无学术性错误偏题怪题,试卷工整是否清晰和标准试题答案准确,是否题量合理老师试做过,试题的内容是否覆盖教材的各个章节,难度适中,区分度,试题的题型多样化合理与课程性质相符合。经统计按学院总体得分如下表
二 SPSS多变量统计
多元线性回归模型是指有多个解释变量的线性回归模型,用于揭示被解释变量与其它多个解释变量之间的线性关系[4]。其数学模型[5]是Y=β0+β1 X1+β2 X2…+βm Xm+ζ(1)上式Y是因变量,代表学生优秀率。X1、X2…Xm是自变量,代表试卷质量中对学生优秀率产生影响的因素。β0为常数项β1、βm是偏回归系数,ζ是随机误差。式中各项系数可通过SPSS软件算出。
三 利用SPSS软件进行分析
(一)软件步骤
通过SPSS软件将学生优秀率作为因变量,其他试卷质量问卷中的8个因素:是否符合教学大纲和专业教学基本要求、有无学术性错误偏题怪题、试卷工整是否清晰和标准试题答案准确、是否题量合理老师试做过、一般试题的内容要覆盖教材的各个章节、难度适中、区分度、试题的题型多样化合理与课程性质相符合作为自变量,
(二)分析结果如下
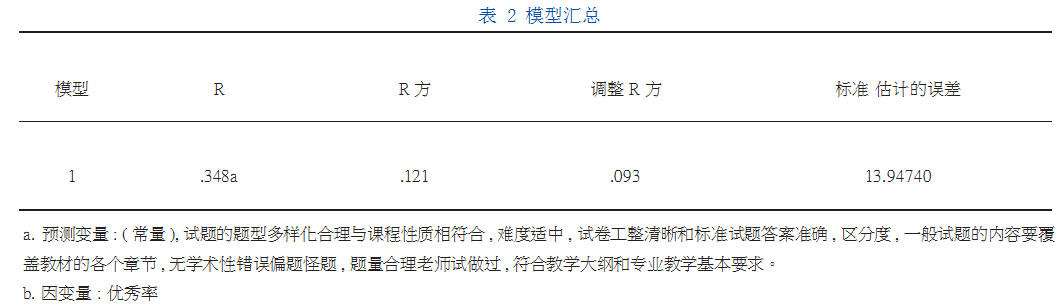
模型汇总表中,R表示拟合优度,是用来衡量模型和观测值之间的拟合程度。它的值越接近1说明模型越好。一般认为,拟合优度达到0.3为中等,图中的最终调整R方为0.093,表示自变量一共可以解释因变量9.3%的变化[6]。
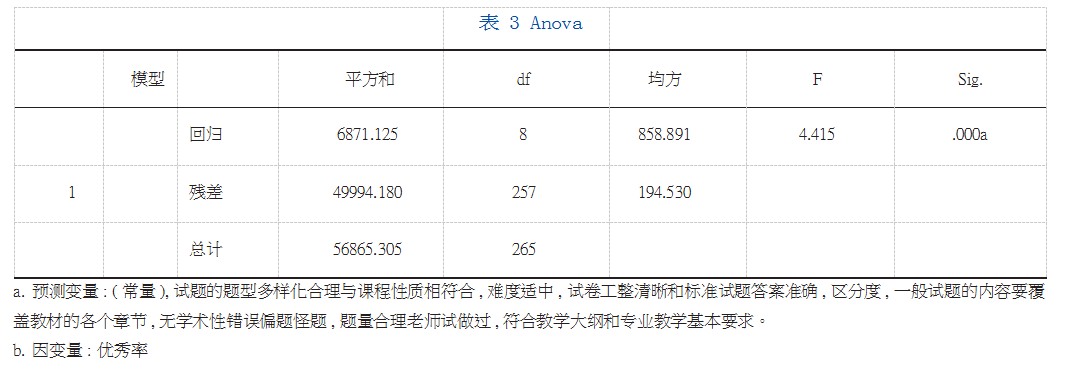
表Anova表示方差分析结果,F值是方差分析的结果,是一个对整个回归方程的总体检验,指的是整个回归方程有没有使用价值,F值对应的Sig值小于0.05就可以认为回归方程是有用的。[7]在本次分析中k为自变量个数8,n为样本容量269,a表示的显著性水平(一般取0.05)。根据查询F值分布表Fa(8,260)值为1.974112964。表中的F值明显大于模型值,则认为各个解释变量对因变量有显著影响作用[8]。根据SPSS分析的系数出了自变量的显著性检验结果,T检验的sig,若数值小于0.05,说明自变量对因变量具有显著影响[9]。
1)常数项的t的显著性概率为0.001<0.05,表示常数项与0有显著性差异,表明常数项应出现在方程中。
2)试卷工整清晰和标准试题答案准确的t的显著性概率为0.003<0.05,表示试卷工整清晰和标准试题答案准确与0有显著性差异,表明试卷工整清晰和标准试题答案准确应作为解释变量出现在方程中。
3)题量合理老师试做过的t的显著性概率为0.002<0.05,表示题量合理老师试做过与0有显著性差异,表明题量合理老师试做过应作为解释变量出现在方程中。
4)难度适中的t的显著性概率为0.000<0.05,表示难度适中与0有显著性差异,表明难度适中应作为解释变量出现在方程中。
四 多元线性回归方程
根据分析之后多元线性回归方程为:Y=23.394+6.5X1-6.926X2+2.068X3 (2)上式中Y是因变量代表学生优秀率;X1、X2、X3是自变量,X1代表试卷工整清晰和标准试题答案准确;X2代表题量合理老师试做过;X3代表难度适中。
五 总结
本文在参考国内外众多学者研究基础上对我校学生试卷调查问卷进行spss多元线性回归分析,从8个试卷质量因素中得出试卷对学生成绩优秀率的3个影响因素。包括试卷工整清晰和标准试题答案准确;题量合理,老师试做过;难度适中。为了让试卷更加的合理化反应出学生的真实水平,因此教师在进行试卷的制作时更加要考虑试卷的清晰度和答案准确性、题量要合理且难度要适中。
参考文献
[1]邱女.影响大学生成绩的因素分析[J].中国市场,2011(26):245-246.
[2]张文颖,张玉,王冉.大学生成绩影响因素的主成分分析[J].科技创新导报,2010(20):175-175.
[3]李晓莉,谷建胜.基于分位数回归的大学生成绩变化实证分析[J].大学数学,2013,29(3):118-123.
[4]杜赫铭,李文.基于SPSS多元线性回归的人才流动分析[J].软件,2017,38(10):149-151.
[5]熊德之,刘为凯,宁小青.基于数理统计的试卷质量分析方法[J].武汉工程大学学报,2007,29(1):78-80.
[6]张宇山.多元线性回归分析的实例研究[J].科技信息,2009(9):54-56.
[7]魏志静,刘希玉,赵庆祯,等.基于SPSS软件与多元线性回归分析理论的分析—分析儿童血液必需元素与血红蛋白浓度的相关关系[J].信息技术与信息化,2006(2):107-109.
[8]杨维忠,张甜.SPSS统计分析与行业应用案例详解[M].清华大学出版社,2013.
[9]李五俊,胡建华.基于Web服务的SPSS与.NET系统集成开发[J].软件,2016,37(4):18-21.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/9773.html