SCI论文(www.lunwensci.com):
摘要:动态几何问题是初中数学的难点.很多学生遇到相关的习题,不知如何加以突破,在各类测试中失分都比较严重.为使学生掌握解答动态几何问题的方法,促进其数学学习成绩的提升,应对初中数学动态几何问题分门别类,认真归纳常用的解题方法,并注重结合具体例题,展示解题方法的具体应用,使其更好的把握解题的细节,在以后的解题中能够举一反三.
关键词:初中数学;动态几何问题;解题方法
初中数学动态几何问题主要的解题思路有:运用函数性质、运用图形性质、借助点的对称、借助图形关系、借助数形结合等进行求解.其中点的对称源于学生所学的“将军饮马模型”,而图形关系则包括图形的全等与图形的相似.教学中仅仅为学生讲解相关理论是不行的,还应注重为学生做好解题方法应用示范.
1借助函数性质求解动态几何问题
动态几何问题情境复杂多变,在求解最值问题时借助函数性质是常用的思路.解题时需在认真审题,吃透题意的基础上,搞清楚角度、线段长度之间的关系,必要情况下设出相关参数,表示出要求解参数的表达式,而后灵活运用一次函数、二次函数以及反比例函数性质进行解答.需要注意的是函数最值与自变量密切相关,因此,应根据题干创设的情境,确定正确的自变量范围.

例1如图1,ABCD为矩形,AB和AD的长分别为10cm,6cm,动点E从A点出发以1cm/s的速度沿AD向点D运动,动点F从点D出发以2cm/s的速度沿DC向点C运动,设运动时间为ts,当S△DEF+S△ABE和最大时,t的值为().
解析该题创设的情境并不复杂,根据点的运动速度可知DE的长度应为AE长度的两倍,如此便将点的运动转化为线段长度.结合已知条件中给出的参数,设出AE的长度后表示出三角形的面积之和,将问题转化为二次函数求最值问题.其中因点E在AD上运动,因此,AE的取值范围为0<AE<6.在该自变量范围内求出二次函数的最值即可.
 2借助图形性质求解动态几何问题
2借助图形性质求解动态几何问题
求解动态几何问题时借助图形性质是经常用到的一种思路.初中数学涉及到的几何图形较多,包括直角三角形、矩形、正方形、圆等,不同的图形有着不同的性质.解题时通过审题明确涉及到的图形,结合线段、角度之间的关系,确定相关对象运动过程中变与不变的量,寻找解题突破口.
例2如图2,在平面直角坐标系xOy中点A、B的坐标分别为(12,0),(0,9),经过点O且和AB相切的动圆和x轴交于点P,和y轴交于点Q,则线段PQ的最小值为().

解析认真审题挖掘题干中的隐含条件.圆在运动过程中∠QOP=90°以及和线段AB相切的关系始终保持不变.由圆的性质可知求PQ的最小值,即求动圆的直径的最小值,如此便将PQ的最小值转化为求最小直径圆的问题.结合O和切点连线的关系可知当圆的直径为AB边上的高时最小.设QP的中点为F,由圆的性质“直径所对的圆周角为90°”可知P,Q应为圆F的直径.问题转化为求过点O且和A B相切圆中直径最小的圆.显然只有当圆的直径是△AOB中AB边上的高才行.因为A(12,0)、B(0,9),则OA=12,OB=9,由勾股定理得到AB=
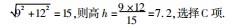 3借助点的对称求解动态几何问题
3借助点的对称求解动态几何问题
求解初中数学动态几何问题的又一种方法即点的对称.其中将军饮马模型是点对称的典型代表.运用点的对称求解动态几何问题应结合题干选取合理的点,并找到对称的线段,必要情况下需结合图形性质确定对称点的具体位置,而后通过做出辅助线,构建特殊图形,如直角三角形,借助勾股定理求出对应线段的长度.
例3如图3,四边形ABCD为菱形,∠D=135°,AD和CE的长分别为

2,在线段AC、AB上分别存在一动点P和F,则PE+PF的最小值是()

解析结合将军饮马模型,寻找点E关于AC的对称点,运用菱形知识确定对称点在线段CD上,不断的改变PF的位置,使P、F、G三点共线,且距离最短.而后做出辅助线构造直角三角形,结合题干中给出的角度与线段长度,求出线段之和的最小值.遇到求解两个线段之和的最小值问题,可从“将军饮马”模型中获得启发,借助点的对称加以求解.设点E关于AC对称的点为G,因四边形ABCD为菱形,因此,点G在DC上.连接PG,BG,过点B作BH⊥CD于H.由菱形性质易得C E=CG=2,PE=PG,要想PE+PF的值最小,即求PG+PF的最小值.点P、F在AC、AB上移动的过程中可知,只有当GPF三点重合时(此时点F和点B重合)的值才最小.由∠D=135°,AD=BC=

易得∠BCD=45°则BH=CH=

cos45°=3,而HG=CH-CG=3-2=1.在Rt
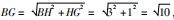
即,PE+PF的最小值是10,选择D项.
4借助图形关系求解动态几何问题
初中数学部分动态几何问题需借助图形关系,寻找角度、线段之间的等量或比例关系.解题常用的知识点有:平行线性质、三角形全等以及三角形相似等.解答该类问题可采用逆向推理法,从要求解的问题切入,分析需要哪些条件,必要情况下做出辅助线更好地揭示要求解问题与已知条件的关系.

例4如图4,在平面直角坐标系中点A、C的坐标分别为(3,4),(x,0),且
且 -2 <x <3,其中B为直线x=-2上的一动点,且满足BC⊥AC,连接A B,
设AB和y轴正半轴所夹锐角为α,则当tanα的值最大时,x的值为().

解析根据题干描述运用直线平行的性质,将角转化到具体的三角形中,表示出角的正切后,将问题转化为求线段BG的最大值.根据题干中给出的已知条件,借助三角形相似,构造线段之间的关系,求出线段BG的最大值.
根据题意分别过点A作AF垂直于x轴,AH垂直于直线x=-2,垂足分别为点F、H.因为y轴和直线x=-2平行,则tanα=AH/BG,又∵AH=5,则tanα=5/BG,当tanα的值最大时,BH的值最小,此时BG的值最大.∵BC⊥AC,则∠BCO+∠CBG=90°,∠BCO+∠ACF=90°,∴∠CBG=∠ACF,△BGC∽△CFA,设点BG=y,则CF=3-x,CG=x+2,又∵BG/CF=CG/AF,

 5借助数形结合求解动态几何问题
5借助数形结合求解动态几何问题
数形结合是初中数学中非常重要的解题思想.解答动态几何问题应用数形结合思想可迅速找到解题突破口.借助数形结合求解动态几何问题,应认真观察给出的图形、图象,通过分析图象中的关键点,如最高或最低点,将其与图形对应起来,充分挖掘图形中的隐含条件.同时,立足几何图形性质求解出相关线段、角度等参数,以达到顺利解题的目的.
例5如图5(a),
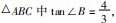
点D
在边BC上运动,过点D向AB引垂线和AB交于点E,取AD的中点为点F,连接EF.当点D从B点出发匀速运动到C点时,y=S△AEF,x=BD,y和x的函数图象如图5(b)所示,则△ABC的面积为()

题目中仅给出∠B的正切值,解题时需读懂图5(b),从中寻找出线段长度.结合x=BD可知,当x值最大值对应BC的长度.找到点D的特殊位置,灵活运用勾股定理以及三角形面积计算公式便可计算出最终结果.

初中数学动态几何问题教学中,为获得良好的教学效果,应结合具体例题运用多媒体技术向学生直观的展示点、线、图形的变化情境,使其能够直观的观察到变与不变的量,尤其在课堂上注重与学生积极互动,营造良好课堂氛围,提升其听课体验的同时,加深其对不同题型的认识,牢固掌握相关的解题方法.
参考文献:
[1]张福宗.试论初中动态几何教学与数学创造性思维的培养[J].中学课程辅导(教师教育),2020(24):5-6.
[2]陈雅怡.浅谈初中数学动态几何教学中对学生创造性的培养[J].新课程,2020(41):192.
[3]黄文凯.数学动态几何问题的教学难点及对策讨论[J].高考,2020(23):67.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/48642.html





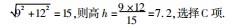

 2,在线段AC、AB上分别存在一动点P和F,则PE+PF的最小值是()
2,在线段AC、AB上分别存在一动点P和F,则PE+PF的最小值是()
 易得∠BCD=45°则BH=CH=
易得∠BCD=45°则BH=CH= cos45°=3,而HG=CH-CG=3-2=1.在Rt
cos45°=3,而HG=CH-CG=3-2=1.在Rt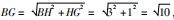 即,PE+PF的最小值是10,选择D项.
即,PE+PF的最小值是10,选择D项.



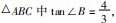 点D在边BC上运动,过点D向AB引垂线和AB交于点E,取AD的中点为点F,连接EF.当点D从B点出发匀速运动到C点时,y=S△AEF,x=BD,y和x的函数图象如图5(b)所示,则△ABC的面积为()
点D在边BC上运动,过点D向AB引垂线和AB交于点E,取AD的中点为点F,连接EF.当点D从B点出发匀速运动到C点时,y=S△AEF,x=BD,y和x的函数图象如图5(b)所示,则△ABC的面积为()