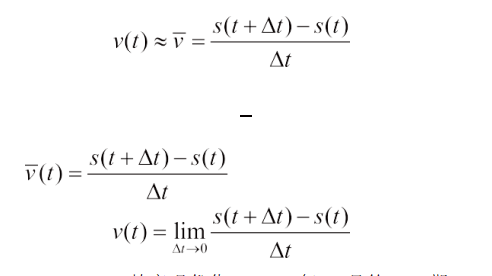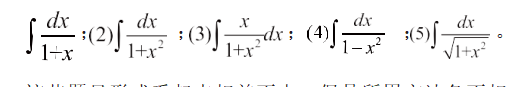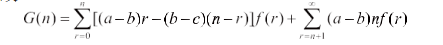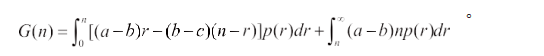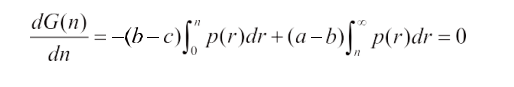SCI论文(www.lunwensci.com):
摘 要:本文根据高等学校课程思政建设指导纲要的要求,在高等数学教学过程中融入思政教育,在讲授知识的同时发挥好育人作用。本文通过介绍数学家的励志故事激发学生的科学钻研和爱国精神,通过分析实例的解决过程培养学生的数学思维,通过适当的数学练习培养学生做人做事的方法,通过案例教学培养学生解决问题的能力, 将思政教育春风化雨般引入高等数学教学过程之中,在潜移默化中提高人才培养质量,实现立德树人的目的。
关键词:高等数学;思政教育;课程教学;探索
本 文 引 用 格 式 : 王 言 英 , 曹 秀 娟 . 在 《 高 等 数 学 》 课 程 教 学 中 融 入 思 政 教 育 的 探 索 [J]. 教 育 现 代化 ,2021,8(41):172-175.
The Exploration of Integrating Ideological and Political Education Into the Teaching of Higher Mathematics
Wang Yanying,CaO Xiujuan(Basic Course Department of Shandong University of Science and Technology,Jinan Shandong)
Abstract: According to the requirements of the curriculum ideological and political construction guidelines in colleges and universities, the paper actively explores the ideological and political elements in higher mathematics curriculum to play a good role in educating students. in the process of higher mathematics teaching teachers can introduce the history of mathematics and the inspiring stories of mathematicians to inspire students’ scientific research and the patriotic spirit, let student sample solution process to develop mathematical thinking , let student do mathematical practice to train the way of doing things, let student solve the practical problem to cultivate the ability to solve problem . ideological and political education is introduced into higher mathematics teaching quietly. in this way, the quality of talent cultivation can be improved subtly, and the purpose of cultivating people with morality can be realized.
Keywords: Advanced Mathematics; ideological and political education; course teaching; explore
一 引 言
《高等学校课程思政建设指导纲要》指出,高校要深化教育教学改革,在教学过程中融入思政教育,发挥好每门课程的育人作用,全面提高人才培养质量。所谓“思政教育”指的是巧妙地将家国情怀、民族意识、匠人精神、职业道德等教育与理论知识融会贯通,在教育学生如何做学问的同时,教给学生如何做一个合格的社会人 [1]。目前已有不少文献进行了有意义的探讨,文献 [1-4] 针对高校化学物理课程的特点深挖德育元素展开思政教学;文献 [5-6]
通过对云南省和上海市高校思政课程的现状进行调查,并提出了相应的策略 [7]。
对高等数学课程思政进行了一些教学探讨。通过课程思政可以引导学生深刻理解中华文化与专业课的关系、国家发展与个人成长的关系 [8]。专业课教师和思政教师深挖专业课程中的思政元素,实现协作育人的目的 [9]。从高等数学作为大学教学中一门重要的公共基础课,在专业建设中有重要作用,也是契合社会现实需要, 培养学生技术应用能力的主干课程。本文依据高等数学课程的特点,深入挖掘高等数学课程教学中思政元素,在传授知识的同时春风化雨般进行德育教育,学生不仅学到知识获得能力,更重要的是教学过程中潜移默化地培养了学生的爱国情怀、勤学苦练,树立正确的人生观、价值观。
二 引入数学家励志的故事,学习他们科学钻研的精神,激发学生的爱国热情
在高等数学教学过程中,恰当引入数学家励志的典型事例,提高学生学习的兴趣,引导学生学习科学探索的精神和激发学生爱国爱家的情怀。教师提前收集古今中外伟大的数学家的优秀事迹,在教学过程中灵活穿插介绍,学习他们科学钻研的精神。比如在学习“极限的概念”时,介绍到利用多边形面积近似计算圆的面积时,也就是“割圆术”,它体现了极限的思想。“割圆术”这个思想就是我国古代的数学家刘徽提出来的。
刘徽是中国数学史上一个非常伟大的数学家,他的杰出代表作《九章算术注》和《海岛算经》是我国最宝贵的数学遗产。刘徽是学而不厌的伟人,一生都在为数学刻苦探求,他虽然地位低下,但人格高尚,他给我们中华民族留下了宝贵的财富。通过学习我国这些数学家们的故事,学生不仅了解了相关的数学思想,还从中学习了伟人的优秀品质,激发学生的爱国热情和民族自豪感,增强民族自信心。作为我们当代的大学生,要树立民族自信心和民族自豪感,要树立为我们的国家争光添彩的目标而奋斗。
再比如介绍微积分的发展史,就不能不提到微积分的创始人牛顿和莱布尼兹这两位伟大的科学家, 他们分别从变速直线运动的瞬时速度(物理问题) 和曲线在每一点处的切线问题(几何问题)两个不同的视角入手,阐述了导数的基本思想。我们不仅学习了数学史,更重要的是学习牛顿、莱布尼兹等科学家们能敏锐地从特殊问题出发抽象总结出里面蕴含的“共性”,并把它提升和确立为微积分理论,这也就是我们现在所说的“特殊到一般”“具体到抽象”的归纳总结能力。通过数学史、数学家的故事, 激励学生也要像科学家那样勤于思考、科学钻研、勇于探索的精神,为我们的祖国贡献自己的力量。
三 将蕴含的数学思想中国的古诗词中引入高等数学的课堂,体会中国传统文化的精髓
在中国古代诗词中有很多诗句体现了数学的某些意境,如“明月松间照,清泉石上流”体现了对称的意境;“孤帆远影碧空尽,惟见长江天际流”体现了极限(或无限)的意境。我国还有许多朗朗上口的古诗词,蕴含着丰富的数学思想。比如在学习有界变量与无界变量时,对于无界变量的理解学生感觉既枯燥又难理解。一句诗句“满园春色关不住, 一支红杏出墙来”体现了微积分教学中的无界变量。无界变量是说,无论设置怎样大的正数 M,变量总要超出你的范围,即有一个变量的绝对值会超过 M。
于是,M 可以比喻成无论怎样大的园子,变量相当于红杏,结果是总有一支红杏越出园子的范围。我国传统文化博大精深,这些优美的诗句中蕴含着丰富的数学思想,在教学过程中引入这些诗词,不仅活跃学生的气氛,使学生易于理解所学的数学知识, 而且让学生体会到了中国传统文化的魅力,使学生养成良好的审美情操。
四 挖掘高等数学中的哲学思想,注重学生的数学思维能力的培养
掌握一定量的知识是培育和发展人类技能和综合能力的基础。但知识不同于能力,尤其是只会应付考试的死知识,根本不是能力;相反,僵死的知识有害于能力的发挥。所以,在高等数学中蕴含着丰富的哲学思想:特殊到一般、一般到特殊、量变与质变等。在教学过程中教师不仅要传授知识,更重要的是通过具体的数学问题培养学生解决问题的思路,从而培养数学思维能力,发现其中蕴含的哲学思想。
在高等数学中有几个非常重要但又很抽象的概念,比如导数、定积分等。这些概念都来自于现实中的特殊问题。例 : 设有一个质点作变速直线运动 , 它的运动规律是 s s(t) ,则它在 t 时刻的速度v v(t) 是什么 [10]?
当我们遇到不知如何求解的问题时,需要思考能否将问题化简,将未知问题转化为已知问题去求解,这是一个重要的数学思想方法。在匀速直线运动中,瞬时速度等于相应时间段内的平均速度;而在变速直线运动中,瞬时速度是随时间变化的,瞬时速度不等于相应时间段内的平均速度,这就是变化与不变、已知与未知的矛盾,我们按照以下思路进行:
第 1 步,在局部很短的时间 t 内用不变代变。在很短的时间间隔 (t, t t) 内,速度 v=v(t) 变化也很小,在时间 (t, t t) 内的变速直线运动近似看做
匀速直线运动,即 t 时刻的速度近似等于这段时间内的平均速度 。
第 2 步, 求 极 限。 时 间 间 隔 t 越 小,
v v(t) 越接近平均速度 v 。当时间间隔 t 0时
的极限就是在 t 时刻的速度 v(t) 。即不难看出 ,这是一个量变过程到质变的飞跃。
这样的例子还有很多,比如曲线在一点的切线的斜率,电流强度等等。去掉这些例子中的具体含义, 抽象出它们都是增量比的极限形式,由此产生了一个重要的数学模型——导数。在讲解这个例子的过程中,就培养了学生的数学思维过程。极限思想是高等数学的核心思想,也是高等数学的精髓。运动变化,质量互变,其中蕴涵着丰富的辩证法,需要我们细细体会。
五 通过高等数学的练习题,培养认真做事、踏实做人的优秀品格
在当今社会,要培养学生的认真做事,踏实做人的优秀品格,通过做数学题就是一种很好的途径。在高等数学中有大量的概念、性质、定理,它们有很强的逻辑关系和使用条件,这些知识点的掌握需要学生在理解的基础上,通过大量的练习,一步步掌握其内涵,来不得半点虚假,要不然会出现“一看就会,一做就错”眼高手低的状况。在学生一道道练习中,使学生养成了踏踏实实、戒骄戒躁、吃苦耐劳的做人做事的优秀品格。比如学习完极限, 我经常给学生出以下四个题:
这里主要考察两点,一个是无穷小的性质,另一个是重要极限 。只有深刻理解其含义,答题才不出错。
再比如不定积分的积分法有多种,计算方法灵活多变,只有通过大量练习才能掌握。例如:(1)
这些题目形式看起来相差不大,但是所用方法各不相同,只有真正理解并掌握才能做对,来不得半点马虎。正如作家格拉德威尔在《异类》一书中指出的“一万小时”定律:“人们眼中的天才之所以卓越非凡,并非天资超人一等,而是付出了持续不断的努力。一万小时的锤炼是任何人从平凡变成世界级大师的 必要条件 [11]。”任何成功没有任何捷径可走,唯有持之以恒勤奋努力。做数学题不仅仅是学习知识,更重要的是在做题中培养自己认认真真做事、踏踏实 实做人、吃苦耐劳的优秀品格,不仅磨练了自己戒 骄戒躁的心性,而且提升了自己的能力。
六 通过案例实践教学,培养学生学习兴趣和学以致用的能力
我们传统的高等数学教学,过分强调数学运算技巧、轻应用,学生就不知道该怎么去利用数学知识解决实际问题。我们为此开辟第二课堂,在课后留给同学与我们的生活息息相关的案例, 让同学去思考如何用所学的知识去解决。比如在学习完利用导数的性质研究函数的最大值、最小值后,让学生根据问题写一份调查报告,阐述采用什么形状的啤酒罐材料最省,还有更好的设计吗?啤酒罐是大学生日常生活中司空见惯的物品,它的形状的设计里还蕴含着这么多的高等数学知识。
这样的问题就抓住了学生的兴趣,让学生在解决实际问题的过程中体会数学的应用价值。另外现在的学生对创业投资问题比较有兴趣,我们所学的知识能不能帮助其实现利益最大化呢?为此在学习完极值及定积分后,给同学留下扩展思考题:
假设某商店只卖一种商品,设每件商品销售价为 a 元,批发价为 b 元,退回价为 c 元, a b c , 问平均每天进货多少件,可使得日平均收入达到最大?(为了问题的简化,我们只考虑进货成本,其他成本不考虑)解决问题的思路 :(
1) 问题分析:每卖出一件商品赚 a b 元;退回一件商品赔 b c 元。若购进商品太多,卖不完的就要赔钱;但是若购进商品少,使得商品不够卖,那么就会少赚钱。我们的目标是购进商品多少时,可以使得长期的日平均达到最大。
(2)问题准备:根据以往的规律,得到每天卖出r 件商品的可能性(频率)为 p(r) 。
(3)建立模型:假设每天购进 n 份,日平均收入为 G(n) 。若 n r, 则所购进报纸全部卖出,可以赚(a b)n ;若 n r, 则卖出的 r 份赚(a b)r ,退回的 n r 份赔(b c)(n r) 元。故 。
现在的目标是求 n,使得 G(n) 达到最大。
(4)离散问题连续化,利用极值求解
由于 r 是正整数,是离散的,不能求导数。因此需要将 n, r 视为连续变量,相应地 p(r) 视为概率密 度 f (r) 。
利用定积分的定义
利用求极值的方法和积分上限函数求导法,得到:
这样的案例使学生明白自己所学知识是可以用来指导实践的,从而学生的学习积极性和兴趣高涨, 而且通过案例提出问题、分析问题、解决问题等环节体验解决问题的全过程,体会从实践中去学习、探索、发现和验证数学规律的意义,培养了自己解决实际问题能力和逻辑推理的能力。
“传道者需先明道”[1] 教师要不断提高自身的德育意识和德育能力,有意识地挖掘高等数学课程中思政元素,采用恰当的教学手段和方法,将思政教育春风化雨般引入高等数学教学过程之中,在潜移默化中提高人才培养质量,实现“立德树人”的目的。
参考文献
[1]王朝霞 , 罗千福 , 徐首红 . 有机化学课程思政教育的现状与应对策略 [J]. 大学化学 ,2019,34(11):45-50.
[2]王旭珍 , 王新平 , 王新葵 , 等 . 大道至简,润物无声——物理化学课程思政的实践 [J]. 大学化学 ,2019,34(11):77-81.
[3]张 树 永 . 高 校 化 学 类 专 业 课 程 思 政 建 设 目 标 与 实 现途 径 刍 议 —— 以 物 理 化 学 课 程 教 学 为 例 [J]. 大 学 化学 ,2019,34(11):4-9.
[4]余江涛 , 王文起 , 徐晏清 . 专业教师实践“课程思政”的逻辑及其要领——以理工科课程为例 [J]. 学校党建与思想教育 ,2018(01):64-66.
[5]陈星宇 , 张春勇 , 王晓燕 . 云南省高校思想政治理论课专题教学资源共建共享模式研究——以云南省 7 所高校为例 [J]. 云南农业大学学报 ( 社会科学 ),2020,14(04):141-146+151.
[6]朱梦洁 .“课程思政”的探索与实践 [D]. 上海外国语大学 ,2019.
[7]孟桂芝 , 姚慧丽 , 钟坦谊 . 基于课程思政的高等数学的教学探索与实践 [J]. 黑龙江教育 ( 理论与实践 ),2021,(03):22-23.
[8]单洁 , 卢光跃 , 田巧娣 . 基于课程思政的教学设计研究与探索[J]. 高教学刊 ,2021,(05):189-192.
[9]路涵旭 . 课程思政视域下专业教师与思政教师协同育人路径研究 [D]. 河北师范大学 ,2020.
[10]同济大学数学系 . 高等数学(第七版)[M]. 北京:高等教育出版社,2014.
[11] 杨水生. 青年教师成长的“力”量[J]. 教书育人,2019(35):54-56.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/32339.html