SCI论文(www.lunwensci.com)
摘要:二维不规则板材排样在工业生产中的应用十分广泛,属于空间布局优化问题。目前该方向的研究主要考虑单规格板材,缺乏在多规格板材上排样不规则零件的研究。提出了一种启发式算法求解二维不规则多规格板材排样问题,该问题需要把不规则零件打包到不同尺寸的板材中,使得所选板材的面积总和最小。为了解决该问题,采用回溯算法和剪枝策略生成板材组合,通过二分搜索策略选定并切换板材组合。对于给定板材组合,提出了基于重叠移除的排样算法,首先通过首次适应下降策略和左下算法尝试把每个零件放置在板材里面,假若还有零件未能放置在板材里面,则运用插入算法把这些零件插入到板材中重叠最小的位置,再通过邻域搜索和重叠移除算法最小化重叠值,从而求得可行解。对多规格板材的算例进行测试,实验结果表明,该启发式算法可有效解决二维不规则多规格板材排样问题。
关键词:切割;下料;不规则板材排样;启发式
A Heuristic for the Two-dimensional Multiple Bin Size Irregular Bin
Packing Problem
Wu Songhuan,Tang Chao,Wei Lijun
(School of Electromechanical Engineering,Guangdong University of Technology,Guangzhou 510006,China)
Abstract:Two-dimensional irregular bin packing is widely used in industrial production,which belongs to spatial layout optimization problem.At present,the research in the direction mainly considers the single-size bins,and there is a lack of research on packing irregular pieces on multiple-size bins.A heuristic is proposed to solve the two-dimensional multiple bin size irregular bin packing problem.The problem requires packing irregular pieces into bins of different sizes so that the total area of the selected bins is minimized.In order to solve the problem,the heuristic uses backtracking algorithm and pruning strategy to generate bin combinations,and then selects and switches bin combinations by binary search strategy.For a given bin combination,a packing algorithm based on overlap removal is proposed.First,try to place each piece in the bin through the first fit decreasing strategy and the bottom-left algorithm.If there are still pieces that cannot be placed in the bin,then use the insertion algorithm to insert these pieces into the position of the minimum overlap in the bin.Then the feasible solution is obtained by minimizing the overlap value through local search and overlap removal algorithm.The instances of the two-dimensional multiple bin size irregular bin packing problem are tested,and the experimental results show that the proposed heuristic can effectively solve the the two-dimensional multiple bin size irregular bin packing problem.
Key words:cutting;packing;irregular bin packing;heuristic
0引言
二维不规则板材排样问题的研究方向通常是把一组不规则零件打包进尺寸唯一的矩形板材中,其目标为最少化使用板材的数量。二维不规则板材排样问题的研究成果被应用于很多行业的实际生产中,例如:钣金加工行业、皮革下料、纺织生产等。根据不同工业应用的需求,该问题会根据零件和板材的属性不同而泛化为不同的变体问题。由于很多工厂都是可以提供不同尺寸的板材给予所需的不规则零件生产的,因此,本文讨论的问题为如何有效地把不规则零件排样在不同尺寸的板材内。为了更符合工厂的实际生产环境,本文假设板材的类型有限,且每种板材的数量也是有限的。在本文中,该问题被称为二维不规则多规格板材排样问题(Two-dimen⁃sional Multiple Bin Size Irregular Bin Packing Problem,2D-MBSIBPP),并提出了迭代加倍二分搜索结合局部搜索的启发式方法来寻找有效的解决方案。
进入21世纪后,越来越多的国内外学者开始对二维不规则排样问题进行研究,该问题可分为二维不规则带排样问题和二维不规则板材排样问题,而本文研究的二维不规则多规格板材排样问题属于二维不规则板材排样问题,目前该方向的研究文献偏少。贾志欣等[1]基于遗传算法对二维不规则零件排样问题进行研究,应用“最低水平线法”将编码转变为排样图,最后有效地求解了二维不规则排样问题。黄红兵等[2]首先离散不规则零件的外轮廓,并适当组合优化每个零件,再求出相对应的包络矩形,然后用矩形排样算法对问题进行求解,形成了不规则排样的二步法。李明等[3]将二维不规则零件的排样问题转化为矩形件的排样问题,并提出一种基于粒子群算法优化求解该排样问题,以此可有效求解二维不规则零件排样问题。刘胡瑶等[4]提出了一种基于重心NFP的二维不规则多边形排样算法来放置不规则零件,并通过顺序递归排样算法和遗传算法调整零件放置顺序来提高原材料利用率。史俊友等[5-6]将遗传算法和小生境技术相结合,以此寻找零件的最优次序,最后用“最低水平线与填充算法相结合”策略的启发式排样算法实现自动排样,在此基础上,他们再提出一种基于小生境遗传模拟退火算法来求解不规则件排样问题的方法,提高了算法的有效性和实用性。张德富等[7]提出了一种基于离散临界多边形模型,该模型在大大降低问题的几何复杂性的同时,也使得许多启发式策略可更容易求解二维不规则排样问题,并证明了基于离散临界多边形模型的排样算法是十分有效的。汤德佑等[8]为提高不规则件启发式排样的材料利用率,提出一种基于重心临界多边形和边适应度的不规则件启发式排样算法。王宏达等[9]介绍了排样布局问题的基本内容,分析并提出了排样算法的未来发展方向。Imamichi等[10]提出了一种迭代的邻域搜索算法来求解二维不规则带排样问题,这种方法主要是通过两个多边形的交换来获取各自的新位置来降低重叠值,并通过基于非线性规划的分离算法来使交错的零件分开来得到有效的整体重叠值减少。基于Imamichi的努力,Leung等[11]在迭代邻域搜索的基础上进行拓展,添加了禁忌搜索算法用来跳出重叠值局部最小这种情况。在此基础上,Elkeran等[12]添加了一个布谷鸟搜索算法来提升搜索范围和效率,并通过把零件组合成一个个零件对来降低计算的时间复杂度。Liu等[13]提出一种改进的鲸鱼优化算法并在一些带排样经典实例上得到了更好的解。随着学者们的不断深入研究,可以发现很多算法、数学模型、几何工具在二维不规则排样问题上都是通用的,Leao等[14]在不规则排样问题上做了一份综述总结,文中提到二维不规则排样问题的一些通用的几何工具以及数学模型。Liu等[15]提出一个用于求解二维不规则板材排样问题的启发式,该启发式用最佳适应策略来分配零件到板材中,并采用左下算法和基于零件交换的邻域搜索来获取和提高排样方案。在此基础上,Zhang等[16]做了相应的优化,分配零件到板材中采用了首次浪费最少策略,排样方案选用的是可热部署的双倍迭代邻域搜索策略,结果显示在各个性能方面都优于之前的结果,并且提高了文献中一大部分经典案例的最优结果。Alves等[17-18]提出一种变邻域搜索算法和一种新的构造算法来求解二维不规则板材排样问题,结果显示他们的算法能比人工找到更好的解决方案。Abeysooriya等[19]为二维不规则多规格板材排样问题生成了一些实例,并针对这些实例提出了有效的邻域搜索启发式算法。
1二维不规则多规格板材排样问题描述与数学模型
1.1问题描述
单规格板材的排样问题常用的评价指标为板材的使用数量,但该指标不能有效评价多规格板材排样问题的可行解,因为多规格板材每个板材其尺寸都可能是不一样的。为了更好评价二维不规则多规格板材排样问题其排样方案的质量,本文采取了评价指标F。
1.2数学模型
二维不规则多规格板材排样问题的特点是根据所供板材的种类和数量,从中选择一组板材给所需排样的零件下料。该问题的目标为最大化所使用板材的原材料利用率,约束为零件之间不可重叠且全部零件必须完全在材料里面。因此,二维不规则多规格板材排样问题的数学模型可构建如下。
其中,由于零件的总面积为定值,则目标函数(2)可优化为最小化所用板材的总面积;约束(3)保证零件之间不可重叠;约束(4)确保零件必须完全在所属的板材之内;约束(5)确保选定的板材其总面积必须大于零件的总面积。
上述的数学模型可支持在问题的求解过程中不断优化解决方案,即在当前板材组合上得到可行解的情况下,为零件在下一个总面积更小的板材组合上寻找可行的排样方案,这就能提高板材的原材料利用率,得到更好的解。
2二维不规则多规格板材排样方法
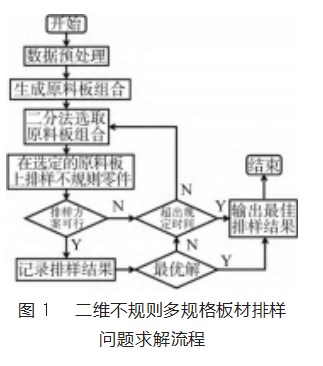
本章将详细介绍用于求解二维不规则多规格板材排样问题的启发式方法,该启发式方法流程如图1所示。首先需要数据预处理,也就是获取所需排样零件和板材的尺寸信息并计算它们各自的面积,并根据零件的总面积产生上界和下界,这个上下界范围指的是选取的板材组合其总面积的范围。然后,在该范围内产生一系列的板材组合为后续的选取板材组合的操作做准备,且板材组合按其总面积从小到大的顺序用一个集合储存。最后,通过二分法来选取板材组合,并在选好的板材组合上排样二维不规则零件,假若规定时间内当前的板材组合可排样成功,下一步则采用总面积更小的板材组合进行排样,否则就采用总面积更大的板材组合进行排样。下面将对板材组合的生成方法、板材组合的选取策略和选定板材的零件放置进行详细地介绍。
2.1板材组合生成方法
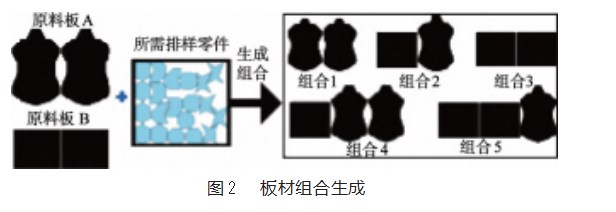
首先,根据零件总面积先制定一个板材组合的总面积范围,假设该零件总面积为s,那么选取的板材组合的总面积必须在[s,2s]这个范围内。该范围也可理解为板材组合的选取范围,因为板材组合的选取是根据该总面积范围选取的。然后,在这个总面积范围内生成板材组合,生成的方法采用了回溯算法和剪枝策略,如图2所示,由板材A和板材B其数量各为两个,一开始生成的板材组合应为:2个板材A、1个板材A和1个板材B、2个板材B。此时,就可以确定板材组合的下界了,该下界就为总面积最小的板材组合——2个板材A。最后,板材组合的上界就确定了,一般情况下,上界可以为[s,2s]范围内面积最大的板材组合,但是这样处理有可能会找不到一个可行解,为了杜绝这种情况的发生,就需要采取另外一种解决方案。这个方案就是对当前[s,2s]范围内那个面积最大的板材组合加板,并采用左下算法生成初始解,直到得到一个可行的初始解为止,加板策略就是从面积最大那个板开始添加,直到数量用完再添加下一个面积最大的板。当得到一个可行的初始解时,此时得到的板材组合就为上界。与此同时,要在板材组合的上下界范围内再运用一次回溯算法和剪枝策略生成还没生成的板材组合,如图2所示,在得到板材组合的上界——1个板材A和2个板材B,还要再生成未生成的原料板组合——2个板材A和1个板材B,即可生成出全部的板材组合。在板材组合生成的过程中,每生成一个板材组合都会按其总面积进行从小到大排序并储存到集合中,为后续板材组合的选取策略做准备。
2.2板材组合选取策略
具体地,在板材组合都生成好了后,就到了选择板材组合的环节了。首先,板材组合的选取策略是一个切换板材组合的过程,而之所以要不断地切换板材组合,其目标就是要不断地寻找利用率高的板材组合,并且不规则零件需无重叠地排样在板材内。切换板材组合的方法本文选择的是二分法,该方法的最大优势就是可以加快获取更优可行解这个过程。如图2所示,由生成了总共为5个并且已经排序好的板材组合,一开始二分法选取的是序号为中间的组合3进行排样,如果排样完后可以得到可行解,那么此时本二分法下一步切换的板材组合为组合2,否则切换的板材组合为组合4,以此类推,直到时间限制时结束并输出找到的最优可行解。总而言之,以上选用二分法的板材切换方法就是板材组合的选取策略了。
2.3选定板材零件放置
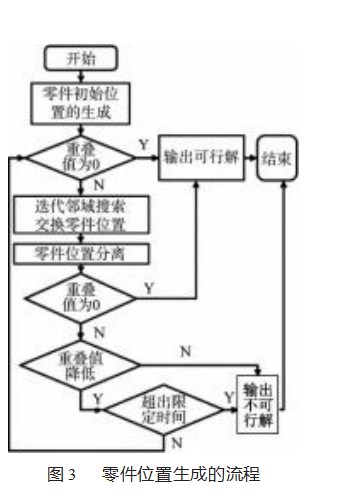
当选定了一组板材后,即可在选择的板材上布局零件的放置位置,该过程可分为3个步骤:零件初始位置的生成、迭代邻域搜索和零件之间的位置分离,其具体流程可如图3所示。需要说明的一点是,本文选用的几何工具为临界多边形,其可为零件生成放置点,为零件提供合适的放置位置。
零件初始位置的生成首先需要应用首次适应下降策略,该策略先根据每个零件的面积从大到小安排放置次序,即优先放置面积大的零件。在零件的放置过程中,在选定的板材组合上优先使用面积大的板材,并结合左下算法把零件无重叠地放置在板材中即为本文采用的首次适应下降策略。但是,并不是每个板材组合都可用这种方法装完所需排样的零件,当遇到不可无重叠放置完零件的情况下,可运用插入算法把没放进板材内的零件插入到板材中。因此,零件初始位置是可以重叠的,当初始位置不重叠时,即可直接输出该排样方案。
随着插入算法的应用,则会产生零件的排样布局为非法解的情况,即零件之间产生重叠或者零件没有完全在板材里面。这时可运用迭代邻域搜索降低排样方案的重叠程度,直到重叠值为0或者达到限定时间为止。迭代邻域搜索主要通过随机交换两个零件的位置来减少重叠值,其具体流程为需先计算零件对集合Pair,该集合用来储存可以两两交换的零件。然后,随机打乱集合中的元素,并根据从集合中依次选择的零件对来进行两个零件的位置交换,从而可以实现随机交换两个零件这个功能,并以此扩大邻域搜索范围。
在每次应用完迭代邻域搜索后,都可以采用分离算法进一步减少排样方案的重叠值,从而可以分离零件,更容易得到一个可行的排样方案。本文采用的分离算法为Imamichi等[10]提出来的,他们构造分离算法的方法可有效率地分离重叠的零件。分离算法的作用其实可把它看成是对弹性势能物理现象的仿真,把不规则零件看成富有弹性的物体,当分离算法一被调用,在板材里面的零件就像是被赋予了弹性这个物理属性,每个零件都可能会因弹力作用而各自相对偏移一段距离,也就是零件之间在相对位置不变的情况下实现了重叠程度的减少。
3实验结果与分析
3.1实验环境
3.2实验数据集
3.3实验结果与分析
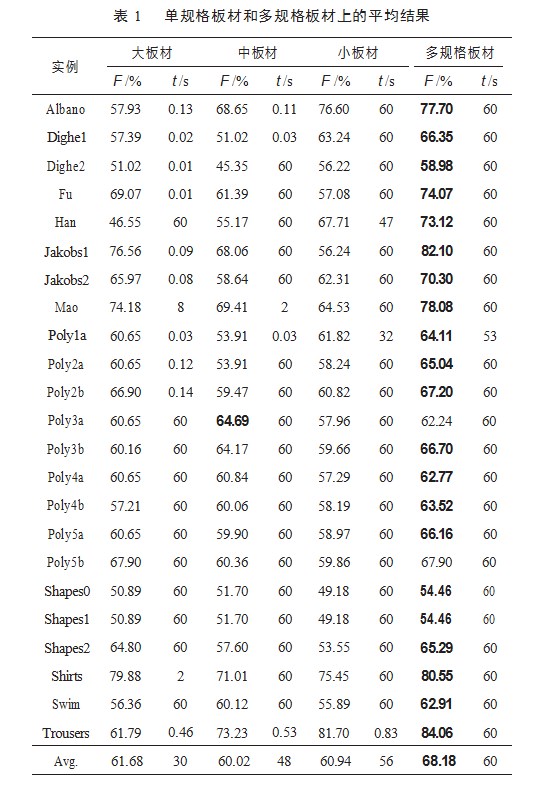
由于本文算法主要应用于解决二维不规则多规格板材排样问题,该问题的特点是板材可以是多种规格的,以及零件可以是凸、非凸的,关键是可不断切换板材组合来提高利用率并求出可行的排样方案。本质上该研究就是要求本算法具有一定的通用性,可应对实际生产中单规格板材甚至多规格板材条件下的二维不规则排样,并且能达到减少原材料浪费的效果,因此本文的平均利用率F值即为零件总面积占所用板材总面积的百分率。下面本文将把实验分为以下4种情况进行,分别为大板材、中板材、小板材和多规格板材,以便测试本算法的性能。
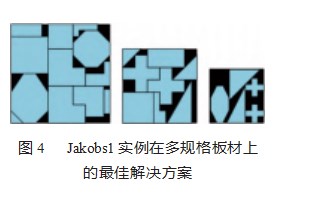
如表1所示,所测试出来的结果对比,可以发现本文的算法不仅可以在单规格的板材中排样零件,在多规格的板材中也是可以排样零件的。两者的主要区别:排样时单规格板材所生成的板材组合数少,切换板材组合的次数少,而多规格板材生成的板材组合数多,且切换板材组合的次数相对也会更多。由实验数据可得知,本文算法在单规格板材中,即3种规格尺寸不一的板材中所得的利用率不相伯仲,而多规格板材上所得的利用率相对地会高许多,这也可进一步验证本实验工作是有意义的。目前,只有Poly3a和Poly5b这两个例子的多规格板材上所得的利用率未能都高于其他3种单规格板材的利用率,但其他例子均是多规格板材所得的利用率为最高,由表1可得多规格板材上的平均利用率为68.18%,均高于其他3种单规格板材的平均利用率,从中也可以看出本文启发式方法的通用性和有效性。图4可见实例Jakobs1在多规格板材上得到的最好的解决方案,其利用率在本文算法的求解下可高达82.10%。
4结束语
本文研究了二维不规则多规格板材排样问题,根据该问题的特点对其进行了充分的问题描述,并构建相应的数学模型对此进行完整的刻画。在分析完问题性质后,本文提出一种启发式方法来解决二维不规则多规格板材排样问题,该启发式方法可分为3个主要部分:板材组合的生成方法、板材组合的选取策略和选定板材的零件放置。通过该启发式方法可成功对所研究的问题进行求解。
通过对多组实例进行实验测试后,从实验结果可以发现,本文算法不仅能应用于单规格板材,还能应用于多规格板材,可看出本文算法是具有一定的通用性的。不仅如此,本文的算法在规定时间内,可在多规格板材中找到比单规格板材利用率更高的解决方案,这也说明了本文提出的启发式方法是具有可行性的。
参考文献:
[1]贾志欣,殷国富,罗阳.二维不规则零件排样问题的遗传算法求解[J].计算机辅助设计与图形学学报,2002(5):467-470.
[2]黄红兵,蒋望东.二维不规则零件排样问题的研究[J].广西科学院学报,2004(4):225-227.
[3]李明,宋成芳,周泽魁.二维不规则零件排样问题的粒子群算法求解[J].江南大学学报,2005(3):266-269.
[4]刘胡瑶,何援军.基于重心NFP的二维不规则形状排样算法[J].中国机械工程,2007(6):723-726.
[5]史俊友,冯美贵.二维不规则件优化排样的小生境遗传算法[J].工程设计学报,2007(2):170-174.
[6]史俊友,冯美贵,苏传生,等.不规则件优化排样的小生境遗传模拟退火算法[J].机械科学与技术,2007(7):940-944.
[7]张德富,陈竞驰,刘永凯,等.用于二维不规则排样的离散临界多边形模型[J].软件学报,2009,20(6):1511-1520.
[8]汤德佑,周子琳.基于临界多边形的不规则件启发式排样算法[J].计算机应用,2016,36(9):2540-2544.
[9]王宏达,尚久浩,樊养余.智能排样算法分析与展望[J].机电工程技术,2004(10):9-11.
[10]IMAMICHI T,YAGIURA M,NAGAMOCHI H.An iterated lo⁃cal search algorithm based on nonlinear programming for the ir⁃regular strip packing problem[J].Discrete Optimization,2009,6(4):345-361.
[11]LEUNG S C,LIN Y,ZHANG D.Extended local search algorithm based on nonlinear programming for two-dimensional irregular strip packing problem[J].Computers&Operations Research,2012,39(3):678-686.
[12]ELKERAN A.A new approach for sheet nesting problem using guided cuckoo search and pairwise clustering[J].European Jour⁃nal of Operational Research,2013(3):757-769.
[13]LIU Q,HUANG Z,ZHANG H,et al.An Enhanced Whale Optimi⁃zation Algorithm For The Two-Dimensional Irregular Strip Packing Problem:Trends in Artificial Intelligence Theory and Applications[C]//Artificial Intelligence Practices:33rd Interna⁃tional Conference on Industrial,Engineering and Other Applica⁃tions of Applied Intelligent Systems,IEA/AIE 2020,Kitaky⁃ushu,Japan,September 22-25,2020,Springer,2020.
[14]LEAO A A,TOLEDO F M,OLIVEIRA J F,et al.Irregular packing problems:A review of mathematical models[J].Europe⁃an Journal of Operational Research,2020(3):803-822.
[15]LIU Q,ZENG J,ZHANG H,et al.A heuristic for the two-di⁃mensional irregular bin packing problem with limited rotations[C]//International Conference on Industrial,Engineering and Other Applications of Applied Intelligent Systems,2020.
[16]ZHANG H,LIU Q,WEI L,et al.An iteratively doubling local search for the two-dimensional irregular bin packing problem with limited rotations[J].Computers&Operations Research,2022,137:105550.
[17]ALVES C,BRAS P,VALERIO DE CARVALHO J M,et al.A variable neighborhood search algorithm for the leather nesting problem[J].Mathematical Problems in Engineering,2012,20121-20128.
[18]ALVES C,BRÁS P,de CARVALHO J V,et al.New construc⁃tive algorithms for leather nesting in the automotive industry[J].Computers&Operations Research,2012,39(7):1487-1505.
[19]ABEYSOORIYA R P,BENNELL J A,MARTINEZ-SYKORA A.Efficient local search heuristics for packing irregular shapes in two-dimensional heterogeneous bins[C]//International Confer⁃ence on Computational Logistics,2017.
[20]MARTINEZ-SYKORA A,ALVAREZ-VALDÉS R,BENNELL J A,et al.Matheuristics for the irregular bin packing problem with free rotations[J].European Journal of Operational Research,2017,258(2):440-455.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/77413.html