SCI论文(www.lunwensci.com)
摘 要:“圆与方程”中与“圆”有关的最值问题是高考的常考问题.为提高学生解答与“圆”有 关最值问题的能力,促进其数学成绩的进一步提升应在对相关问题认真归类的基础上,做好经典习 题的讲解,给学生更好地解答类似问题带来良好启示.
关键词: 高中数学,圆,最值问题,例讲
与“圆”有关的最值问题解题思路灵活多变,其中函数视角、图形视角、对称视角、坐标视角、向量视角是解题的常用视角.不同视角适合分析的问题类 型不同,解题细节存在较大差别,为使学生掌握不同解题视角的关键,教师应以经典例题为载体展开教 学活动.
1 基于函数视角解题
基于对函数单调性的认识与理解不难发现,运 用函数单调性解题时关键需把握两点: ( 1) 构建正 确的函数类型; ( 2) 以函数为依托探讨最值问题需 围绕自变量开展.能否正确地确定自变量范围,关系 着求解结果的正确性,需根据习题情境以及实际情 况,因此,应认真确定自变量的上限与下限.
2 基于图形视角解题
借助圆的方程可实现对圆心、半径的准确刻画, 解决与圆相关的一些问题.但是对于与“圆”有关的 最值问题仅仅使用代数方法,有时不仅无法直观地洞察圆与其他对象之间的关系,而且陷入计算繁琐 的境地.事实上,从几何角度来看,圆不仅是轴对称 图形,而且是中心对称图形,并且学生已经系统学习 过与圆相关的定理、性质,从图形视角解答最值问题 有时会获得意想不到的效果.
3 基于对称视角解题
基于对称视角解答与“圆”有关的最值问题,首 先应突破如何寻找对称关系这一重点.寻找对称关 系基于相关经验以及对图形关系的深入洞察,尤其 需思考找到“对称”对象后接下来该怎么处理,是否实 现了化难为易的目的.根据经验,经过“对称”处理后, 最值点往往出现在点的共线上,并且这一共线关系和一些圆的圆心关系密切.在这一方向指引下不难寻找 到正确思路,接下来只需认真计算即可.
4 基于坐标视角解题
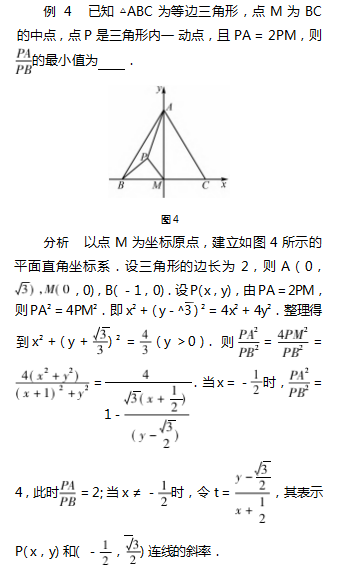
对于与“圆”有关最值问题的求解,可根据实际 情况从坐标视角进行分析,通过坐标计算与图形关 系的结合不难寻找到解题思路.众所周知,平面图形 中点的坐标与平面直角坐标系位置密切相关.为降 低计算复杂度应首先依托现有的图形、线段关系构 建平面直角坐标系.在此基础上合理设出相关参数, 对相关点的位置加以准确刻画.根据经验一些点的 位置往往是动态变化的,其轨迹会形成一个圆或圆 的一段弧.对于圆弧而言可借助圆的方程以及对应 参数范围加以限定.以此为基础充分利用题干中的已知条件逐渐向要求解的问题靠拢,直到经过运算 能够运用熟悉的知识顺利得出结果.
5 基于向量视角解题
向量与线段的区别在于向量具有方向性,使得其运算必须遵循自身的法则,但是向量的模与线段 的长度是统一 的.针对这一情况,可从向量视角解决 一些与“圆”有关的最值问题.一般情况下,基于向 量视角解决与“圆”有关的最值问题时,一般题干中 都会有提示,如以向量的形式给出已知条件或者要 求与向量相关的最值等.当然仅仅知道这一点是不 行的,需充分运用已知条件通过抽象、运算、整理等 处理,使得一些隐含的关系清晰地展示出来,为向量 知识的运用做好铺垫.
综上所述,高中数学与“圆”有关的最值问题是 非常重要的一类问题.该类问题又被进一步细分为 多种情境,而且不同情境应用的解题思路有时存在 较大差别.实践中为使学生能够举一反三,实现解题 能力以及解题灵活性的提升,在做好相关情境类似 问题的基础上讲解常用的解题视角,并依托习题做 好各视角在解题中的应用展示,鼓励学生多思考、多揣摩,将相关细节理解到位,把控到位.
参考文献:
[1] 张志刚.例谈直线与圆 中的最值问题 [J].中学数学,2017( 23) : 58-60.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/63076.html