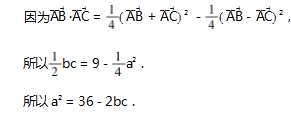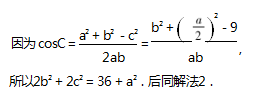SCI论文(www.lunwensci.com)
摘 要: 本文通过研究一道解三角形习题,梳理了三角形面积最值问题的不同求解视角,低起 点高站位,所用知识均源于课本,以学生视角探索解题思路.
关键词: 解三角形,面积公式,平面向量
试题呈现
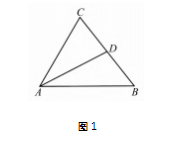
例 1 如图 1.已知 a,b,c 分别为△ABC 三个内角 A,B,C 的对边,D 是 BC 的中点,且 AD = 3.A =π/3.求 S△ABC 的最大值.
2 试题解析
思路 1 向量法.
结合图形,构造向量表达式,平方可以将向量运 算转化为模长运算,得到三角形边的关系,通过均值 不等式求解即可.
解法 1 向量图形运算.
解法 2 向量图形运算.
解法 3 极化恒等式.
后同解法 2.
极化恒等 式 是 将 向 量 点 积 运 算 转 化 为 三 角 形边长运算的重要课本结论,尤其是本题这种涉 及中线长的问题,通过该式可以快速建立运算表 达式.
思路 2 以角为纽带联系边长.
解法 4 互补的角.
互补两角的正弦值相等,余弦值相反在解三角 形中是很常用的,比如证明“角分线性质”时就可以 用该方法.问题如下:
已知: a,b,c 分别为△ABC 三个内角 A,B,C 的 对边,AD 是∠A 的平分线.求证AB/AC=BD/BC,同学们快来试试吧.
解法 5 算两次.
△ABC 与△ADC 内都有∠C,分别在两个三角 形中应用余弦定理,以 ∠C 为纽带联系边长关系属 于“算两次”的思想.该方法适用于有两个不同的三 角形共用其中的边或角的情况,既可以通过角算两 次,也可以通过边算两次.
思路 3 利用教科书结论直接寻找边长关系.
人教 A 版教科书必修二第 39 页例 2 证明了 “平行四边形对角线平方和等于四条边平方和”.本 题可以“倍长中线”构造一个口ABEC,再利用上面 结论解答.
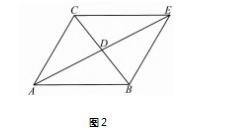
解法 6 如图 2.延长 AD 至点 E 使 AE = 2AD. 由上述课本结论得2 AB2 + 2 AC2 = AE2 + BC2.即 2b2 + 2c2 = 36 + a2.后同解法 4.
该课本结论,证明简单、应用方便,其变形形式 即为“中线长定理”.人教 A 版教科书必修第二册53 页 15 题给出了该公式:
△ABC 的三边分别为 a,b,c,边 BC,CA,AB 上 的中线分别记为 ma,mb,mc,利用余弦定理证明
证明略.
思路 4 坐标法.
建立平面直角坐标系,可以将几何问题转化 为代数运 算,通 过 向 量 的 坐 标 运 算,或 者 直 线 方 程等解析 几 何 的 研 究 方 法 快 速 解 决 问 题,当 然,建系的方法不唯一,本题为了应用 A =π/3,所以选择了如下建系方式:
综上所述,本题在△ABC 是等腰三角形时取到 最大值,解题方法众多,但也可以看出,向量方法明 显是更为行之有效的,可能这就是教科书没有把解 三角形的知识放在必修一 中,而是放在必修二的向 量章节中的原因吧.
四种解题思路也是处理解三角形问题的常用方 法,另外,同学们还要关注教科书中的常用结论,宝藏多多,等待大家挖掘.
参考文献:
[1] 中华人民共和国教育部.普通高中数学课程标准( 2017 年版 2020 年修订) [M].北京: 人民教 育出版社,2020.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/62953.html