SCI论文(www.lunwensci.com):
摘要:针对蚁群算法在智能车辆避障路径规划中存在拐角多、收敛速度慢的问题,通过对基本蚁群算法的启发函数和信息素浓度更新模型改进,提出一种基于A*蚁群融合算法的避障路径规划方法。首先,利用A*算法估价函数和转弯拐角惩罚因子,构造了一种增强型启发函数,以引导算法对目标点的感知,减少路径搜索的盲目性,提高规划路径平滑度;其次,提出一种基于拐角惩罚因子的自适应信息素浓度增量模型,以提高全局收敛速度。最后通过基于复杂障碍环境的栅格地图仿真分析证实了算法的有效性。
关键词:蚁群算法;避障;路径规划;栅格地图
A Research on Obstacle Avoidance Path Planning Based on Ant Colony Algorithm with A ∗ Heuristic Method
Sheng Hongqiang1, Huang Haiying2, 3, Cui Yigang1
( 1. China National Heavy Duty Truck Group Power Co., Ltd., Jinan 250101, China; 2. School of Mathematics and Statistics,Wuhan University,
Wuhan 430072, China; 3.Shandong Shenghan Finance and Trade Vocational College, Jinan 250316, China)
Abstract: To solve the problems of many corners and slow convergence speed of ant colony algorithm, an obstacle avoidance path planning method based on A*ant colony algorithm was proposed for autonomous vehicles by improving the heuristic function of basic ant colony algorithm and pheromone concentration update model. Firstly, constructed an heuristic functionbased on A* algorithm evaluation function and corner penalty factor to enhance the perception of ant colony algorithm to the target point and reduce the blindness of path search and improve the smoothness of the planned path. Secondly, proposed an adaptive pheromone concentration increment model based on corner penalty factor, to improve the global convergence of the algorithm. Finally, proved the effectiveness of the algorithm by simulation analysis based on complex obstacle environment of the grid map.
Key words: ant colony algorithm; avoiding obstacles; path planning; grid map
0 引言
智能车辆是一个集环境感知、规划决策和轨迹跟踪 控制等功能于一体的综合系统。随着新一代人工智能技 术的快速发展, 智能车辆已成为未来汽车产业的重要发 展方向。避障路径规划是智能车辆领域的关键技术之一, 是当前国内外学者研究的热点[1-5]。
智能车辆避障路径规划一般是指在障碍物环境中, 满足路径平滑度最高、距离最短、能耗最小等约束条件 下, 从车辆起始点到目标点规划出一条无碰撞路径。路 径 规 划 算 法 主 要 有 人 工 场 势 法[6] 、 概 率 路 图 法 ( PRM) [7]、快速随机拓展树法 (RRT) [8]、几何曲线插 值法[9] 、D*算法[10] 、A*算法[11]、蚁群算法[12-16]、粒子群 算法[17]等。智能车辆安全行驶对路径规划算法效率、路 径平滑性提出了较高的要求, 而每种路径规划算法适用领域不同, 导致单算法结构不具有泛化求解能力, 往往 针对具体问题需要进行优化整合。蚁群算法是由意大利 学者 M Dorigo 等[14]于 1996年提出, 它源于模拟蚁群觅食 行为完成寻路过程, 通过残留信息素计算路径节点选择 概率, 最终得到优化的规划路径。蚁群算法鲁棒性强, 易于与其他优化算法相结合, 实际应用中存在规划路径 不光滑、路径曲折和收敛速度慢的问题[18-20]。
针对上述蚁群算法存在的缺陷, 本文通过对蚁群算 法启发函数和信息素更新策略改进, 提出一种适用于智 能车辆的基于 A*蚁群融合算法的避障路径规划方法。该 方法不仅融合 A*算法估价值和转弯拐角约束条件, 构造 了一种增强型启发函数, 还设计改进了信息素浓度增量 模型。仿真结果表明, 本文算法在改善规划路径平滑度 和算法性能方面效果明显。
1 蚁群算法
由于蚁群算法原理在 M Dorigo 等人的著作已有详尽 的描述, 在此不做赘述。蚁群算法的核心是利用状态转 移概率和信息素更新策略实现路径选择。
1.1 状态转移概率
迭代过程中, 蚂蚁 m ( m=1, 2, 3, …, M) 在 t 时 刻从当前节点 i 转移到下一节点j 的状态转移概率由路径 上的信息素浓度和两点间的距离启发函数确定。状态转 移概率表达式如下:
P (t) =〈
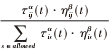
if s ∈ Um ( 1)
■0, else
U = U - Tabu
式中: P (t)为 t 时刻第 m 只蚂蚁从当前位置节点 i 到相邻 位置节点j 的状态转移概率; τij (t) 为路径 (i, j) 上的信 息素浓度; η ij (t) 为蚂蚁 m 在节点 i 处选择下一节点j 的启 发函数, 反映边 (i, j) 的能见度; α 为信息启发式因子, 反映信息素对蚂蚁选择路径的影响力; β 为期望启 发式因子, 反映启发式信息在指导蚁群搜索过程中的相 对重要程度; U 为路径所有节点的集合; Um 为蚂蚁尚未 访问节点的集合; Tabum 为已访问节点的集合; s 为节点 i 相邻的可选节点的集合; τis (t) 为节点 i 与各相邻节点之 间的信息素浓度; η is (t) 为蚂蚁在节点 i 与各相邻节点之 间的启发函数。
蚁群算法启发函数ηij (t)表达式为:
η ij (t) = 1/dij ( 2)
式中: dij 为节点 i 和j 之间的距离, 即:
dij =
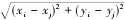
1.2 信息素更新策略
当所有蚂蚁完成一次迭代后, 需对路径信息素进行更新, 其更新公式为:
τij (t) = (1 - ρ ) ⋅ τij (t - 1) + Δτij ( 3)
Δτij =
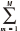
Δ
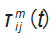
(t)
式中: τij (t) 为 t 时刻节点 i 到下一节点j 路径之间的信息 素浓度; τij (t - 1) 为在 t-1 时刻节点 i 到下一节点j 路径之 间的信息素浓度; ρ 为信息素挥发系数, ρ ∈ (0, 1); Δτij 为 M 只蚂蚁完成一次迭代, 边 (i, j) 上累积残留的信 息素浓度; Δτ (t) 为第 m 只蚂蚁完成一次循环边 (i, j) 上残留的信息素浓度。
M Dorigo 等人提出 3种不同的信息素浓度增量模型, 分 别 称 之 为 Ant-Density System ( ADS)、 Ant-Quantity System (AQS) 和 Ant-Cycle System ( ACS) 模型。
若 第 m 只 蚂 蚁 当 前 循 环 经 过 边 (i, j) 的 集 合 为 X {(i,j ) | i = 1, 2, …,n ; j = 1, 2, …,n | }, 则 信 息 素 浓 度 增 量模型函数Δτ (t)表示如下。
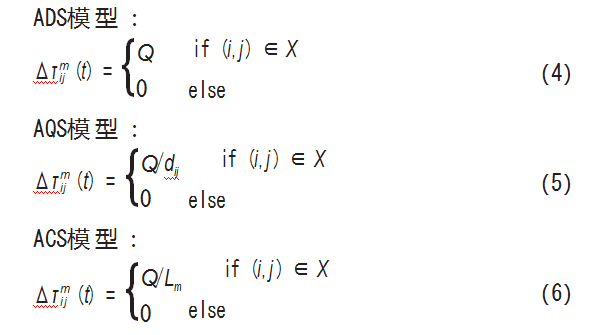
式中: Q 为信息素强度, 影响算法求解速度, 为大于零 的常数; Lm 为第 m 只蚂蚁在本次循环中所经过路径的总 长度。
上述 ACS模型采用的是全局更新策略, 蚂蚁完成一 个循环后再更新残留信息素的浓度, 在求解路径规划问 题中最为常用, 因此本文采用该模型作为信息素更新的 基本模型。
2 改进蚁群算法
由于蚁群算法启发函数ηis (t) = 1/dij 仅利用相邻节点 的信息, 全局启发性不足, 易出现规划路径拐角多、盲 目搜索和收敛速度慢问题。下面从启发函数和信息素更 新策略两方面对算法进行改进。
2.1 构造基于A*算法的启发函数
A*算法是一种启发式搜索算法, 其核心是利用估价 函数在状态空间中从起始点开始对每一个搜索位置进行 评估, 按照评价准则 (如路径最短或消耗最小等指标) 选取最优的位置, 再从这个位置进行搜索直到目标位置。 以最短路径作为搜索评价指标, A*算法估价函数的可表达式为:
F (n ) = G (n ) + H (n ) ( 7)
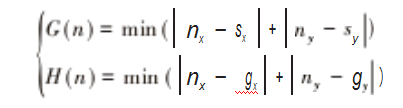
式中: n 为起始节点相邻的节点; F ( n ) 为节点 n 的估价 函数; G ( n ) 为在状态空间中从初始节点 s 到节点 n 的最 短距离; H ( n ) 为从节点 n 到目标节点 g 的最短距离; nx 为节点 n 的横坐标; ny 为节点 n 的纵坐标; sx 为起始节 点的横坐标; sy 为起始节点 s 的纵坐标; gx 为目标节点的横坐标; gy 为目标节点 g 的纵坐标。
引入 A*算法估计代价 F ( n ) 和拐角惩罚函数f (θij ) 作为蚁群算法启发函数的启发因子, 改进后的蚁群算法 启发函数表达式如下:
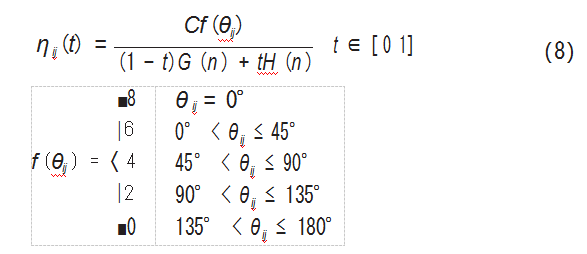
式中: t 为目标节点g 影响路径选择的权重; θ ij 为从节点 i 经过相邻节点j 转过的角度;f (θij )为节点 i 与节点j 之间 的拐角惩罚函数; C 为惩罚函数系数, 为一常量。
2.2 改进信息素浓度增量模型
利用蚂蚁当前路径、最优路径和最差路径, 以及将 当前迭代路径累积拐角惩罚函数, 优化信息素浓度增量 模型。优化后的信息素浓度增量模型表达式如下:
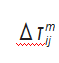
(t) =
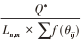
( 9)
Q ∗ =
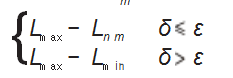
式中: Q* 为信息度浓度的强度值; n 为当前迭代次数; Ln, m 为当前路径长度, 即第 m 只蚂蚁产生的路径的长度; Lmin 为最优路径长度, 即第 n 次迭代产生的最短路径长度;Lmax 为最差路径长度, 即第 n 次迭代产生的最长路径长度;
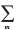
f (θij )为当前迭代最短路径上各点拐角的累积惩罚值; δ为路径偏离值, δ = Lmax - Ln,m, 即最差路径的长度与当前 路径长度之间的差值; ε 为第 n 次迭代路径允许误差。
在迭代过程中, 新的信息素增量机制可以自适应动 态调整信息素的强度, 使优化过程加速向全局最优路径 收敛。当 δ > ε 时, Lmax 与 Ln, m 差值越大, 信息素强度越 大, 全局收敛时间缩短, 算法求解效率得到提升; 当 δ ≤ε 时, Ln, m 与 Lmin 越接近, 信息素浓度蒸发越快, 使算法避免出现过早收敛陷入局部最优。引入
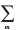
f (θij ), 保证迭代过程中拐角最小路径上的信息素浓度得到加强, 利于改善路径平滑性。
2.3 改进算法步骤
本文提出的基于 A*蚁群融合算法的避障路径规划方 法算法步骤如下。
( 1) 创建栅格地图环境。选择起始点和目标点。
( 2) 初始化参数: 蚂蚁规模 M, 最大迭代次数 N, 信息启发式因子 α, 期望启发式因子β, 信息素挥发系数 ρ 等。设定初始迭代次数 n=1 ( n=1, 2, 3, …, N), 初 始蚂蚁编号 m=1 ( m=1, 2, 3, …, M), 并把起始点 S 置入禁忌表 Tabu。
( 3) 路径选择。访问 um 查找当前节点前往下一步可 行节点, 按式 ( 1) 和 (8) 分别计算下一步可行节点的概率, 然后, 按轮盘法选择下一节点。将选定的下一节 点作为新的起始点即当前节点, 更新禁忌表 Tabu。
( 4) 蚂蚁序号更新。若第 m 只蚂蚁的当前节点列表 包含了目标点或无路径且 m≥M, 则转入步骤 5; 否则, m=m+1, 返回步骤 3。
( 5) 信息素更新。计算当前迭代最优路径并按式( 3) 和 (9) 更新信息素浓度。
( 6) 迭代或停止。若 n≥N, 则输出最优路径并停止
迭代; 否则, n=n+1, 释放禁忌表 Tabu, 返回步骤 3。 3 仿真分析
3.1 仿真环境地图模型
本文采用栅格法构建工作空间地图模型, 栅格法是 将智能车辆行驶的空间分解成 N×N 具有二值信息的网格 单元。下面以 10×10栅格地图为例, 简要说明栅格地图 模型表示方法, 如图 1所示。
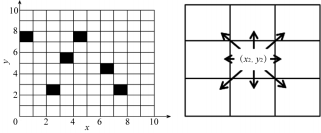
图 1 栅格地图 图 2 八个可行方向
图 1 中黑色占有的栅格表示障碍物, 白色占有的栅 格是可行栅格。按从左到右, 从上到下的顺序, 依次为 栅格进行编号, 栅格中心的坐标为直角坐标, 则栅格地 图中的任意一点的坐标 ( xi, yi ) 与栅格编号 i 的映射关 系如式 (10) 和式 (11) 所示:
xi = a ⋅ (mod(i,N × N ) - 0.5) (10)
yi = a ⋅ (MM + 0.5 - ceil (i/N × N )) (11)
式中: a 为栅格边长; N×N 为栅格编号数值最大的值; mod(a, b)为 ( a/b) 取余结果; ceil 函数为朝正无穷大方向 取整。
被控对象在某一个栅格内可到达的栅格有与其相邻 的上、右、下、左、右上、右下、左下、左上 8个方向上的栅格, 如图 2所示。
3.2 仿真结果分析
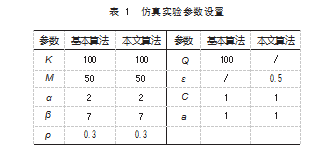
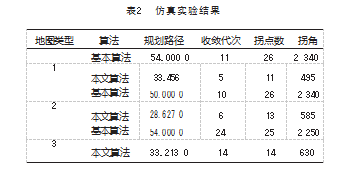
为了验证改进蚁群算法的有效性, 本文通过仿真程 序, 在 3种复杂障碍物环境栅格地图 (20×20) 下, 对基 本蚁群算法和本文改进蚁群算法进行了仿真对比分析。 仿真试验参数设置如表 1所示。仿真结果如图 3~5 和表 2 所示。
图 3 是在地图 1 环境下仿真结果, 是基本蚁群算法和本文提出的改进蚁群融算法的避障路径规划图和迭代收敛曲线。如表 2所示, 本文改进蚁群算法较基本蚁群算法迭代收敛速率提高了 54.55%, 最优路径减少了 38.04%, 拐点数减少了 57.69%, 路径平滑度即拐角之和提高了 78.85%。
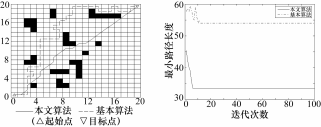
( a) 最短路径规划图 (b) 迭代收敛变化曲线
图 3 基于地图1环境下两种算法最短路径规划图和迭代收敛变化曲线
图 4是在地图 2环境下仿真结果, 如表 2所示, 本文 改进蚁群算法较基本蚁群算法迭代收敛速率提高了 40%, 最优路径减少了 42.75%, 拐点数减少了 50%, 路径平滑度即拐角之和提高了 75%。
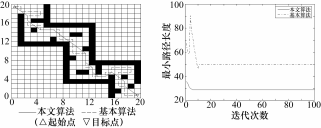
( a) 最短路径规划图 (b) 迭代收敛变化曲线
图 4 基于地图2环境下两种算法最短路径规划图和迭代收敛变化曲线
图 5是在地图 3环境下仿真结果,如表 2所示, 本文改进蚁群算法较基本蚁群算法迭代收敛速率提高了
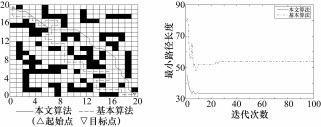
( a) 最短路径规划图 (b) 迭代收敛变化曲线
图 5 基于地图 3环境下两种算法路径规划图和迭代收敛变化曲线
45.41%, 最优路径减少了 38.49%, 拐点数减少了 44%, 路径平滑度即拐角之和提高了 72%。
综合上述 3 种地图环境下两种算法的仿真结果, 本 文改进的蚁群算法即 A*蚁群融合算法较基本蚁群算法环 境适应能力强, 迭代收敛速率平均提高了 41.67%, 最优 路径减少了 39.76%, 拐点数减少了 50.56%, 路径平滑度即拐角之和提高了 75.28%。
4 结束语
基本蚁群算法在智能车辆避障路径规划中存在拐角 多、收敛速度慢、泛化求解能力差等问题, 本文通过对 基本蚁群算法改进, 提出一种基于 A*蚁群融合算法的智 能车辆避障路径规划方法, 仿真结果显示改进效果良好。 特别是在算法收敛速度、最优路径和路径平滑度等方面 改进效果明显。引入 A*算法估价因子和路径拐角惩罚因 子, 构造的增强型启发函数在引导蚂蚁对引导目标节点 的感知、消除路径搜索的盲目性和提高路径平滑度方面 作用明显; 提出的基于拐角惩罚因子的自适应信息素浓 度增量模型, 可以动态调整信息素浓度的强度使算法快 速向转角最小的最优路径收敛。
参考文献:
[1] 李永丹,马天力,陈超波, 等 . 无人驾驶车辆路径规划算法综述 [J]. 国外电子测量技术,2019, 38(6):72-79.
[2] 熊璐,杨兴,卓桂, 等 . 荣无人驾驶车辆的运动控制发展现状综 述[J].机械工程学报,2020, 56(10):127-143.
[3] 任丽军, 刘元盛, 柴梦娜 .基于无人车避障路径规划方法的综 述[J]. 计算机科学,2018,45(10A):203-205.
[4] Jiang Yan,Gong JianWei,Xiong GuangMing. Research on diferen ‐ tial constraints-based planning algorithm forautonomous-driving vehicles[J].Acta Automatica Sinica,2013, 39(12):2012−2020.
[5] 韩月起,张凯,宾洋, 等 .基于凸近似的避障原理及无人驾驶车 辆路径规划模型预测算法[J]. 自动化学报, 2020,16(1):153- 167.
[6] 张家旭,王晨,赵健 . 基于改进人工势场法的汽车弯道超车路 径规划与跟踪控制[J]. 汽车工程,2021, 43(4):546-552.
[7] 田洪清,王建强,黄荷 . 叶越野环境下基于势能场模型的智能车概率图路径规划方法[J].兵工报,2021,42(7):1496-1505.
[8] 董敏,陈铁桩,杨浩 . 基于改进 RRT 算法的无人车路径规划仿真研究[J]. 计算机仿真, 2019,36(11): 96-100.
[9] Chen L, Qin D, Xu X, et al. A path and velocity planning method for lane changing collision avoida-nce of intelligent vehicle based on cubic 3D Bezier curve[J].Advances in engineering soft ‐ ware,2019(132):65-73.
[10] 刘晓涛,蔡云飞,王田橙 . 基于 SVM 的受约束 D*算法在无人 车寻路中的应用[J]. 计算机与数字工程,2017, 45(9):1748- 1754.
[11] Song Rui,Bucknall Richard,Liu Yuanchang.Smoothed A* algo ‐ rithm for practical unmanned surface vehicle path planning[J]. Applied Ocean Research,2019.839~20.
[12] 李明龙,李清忠 . 基于改进蚁群算法的无人天车路径规划[J]. 计算机仿真,2021, 38(8) 172-176.
[13] 贺智明,郑丽,梁文 .基于自适应动态搜索蚁群算法的车辆路 径规划[J]. 计算机工程与设计,2021,42(2):543-551.
[14] M Dorigo,V Maniezzo, A Colorni.The ant system: Optimization by a colony of cooperating agents [J]. IEEE Transactions on Sys ‐
[15] 覃远年,梁仲华 .蚁群算法研究与应用的新进展[J]. 计算机工 程与科学,2019,41(1):173-184.
[16] 蓝丹,樊东红,陈强 . 改进的蚁群算法在智能车辆路径规划中 的运用[J]. 组合机床与自动化加工技术, 2021(4):130-133.
[17] 刘晓欢,张德干,张捷, 等 . 一种基于粒子群优化改进策略的 智能驾驶车辆路径规划方法[J]. 北京交通大学学报,2020, 44 (5):87-97.
[18] 赵又群,闫茜,葛召浩, 等 .基于改进蚁群算法的汽车避障路 径规划[J]. 重庆理工大学学报(自然科学版),2020, 34(4): 1-10.
[19] 胡立华,马瑞,张明师, 等 .基于改进蚁群算法的智能小车路 径规划方法[J]. 太原科技大学学报,2020,41(6): 463-468.
[20] 卢宇凡,张莉 .基于粗糙集和蚁群算法的机器人路径规划研 究[J]. 计算机与数字工程,2012,40(12):7-9.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/45418.html
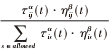 if s ∈ Um ( 1)
if s ∈ Um ( 1)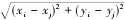
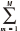 Δ
Δ 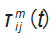 (t)
(t)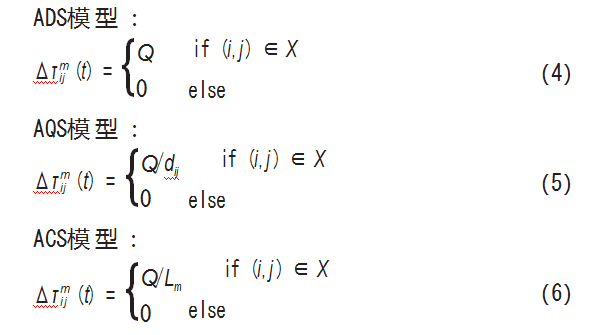
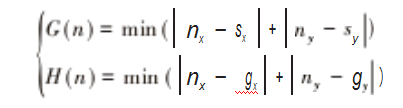
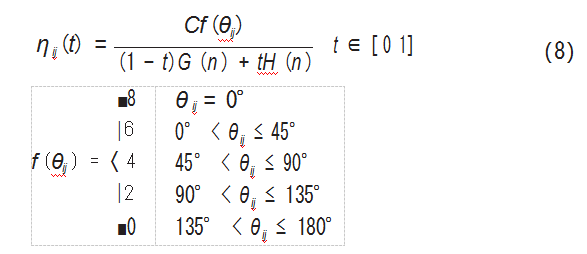
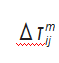 (t) =
(t) =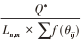 ( 9)
( 9)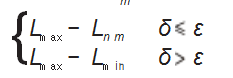
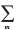 f (θij )为当前迭代最短路径上各点拐角的累积惩罚值; δ为路径偏离值, δ = Lmax - Ln,m, 即最差路径的长度与当前 路径长度之间的差值; ε 为第 n 次迭代路径允许误差。
f (θij )为当前迭代最短路径上各点拐角的累积惩罚值; δ为路径偏离值, δ = Lmax - Ln,m, 即最差路径的长度与当前 路径长度之间的差值; ε 为第 n 次迭代路径允许误差。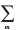 f (θij ), 保证迭代过程中拐角最小路径上的信息素浓度得到加强, 利于改善路径平滑性。
f (θij ), 保证迭代过程中拐角最小路径上的信息素浓度得到加强, 利于改善路径平滑性。