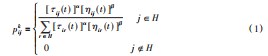SCI论文(www.lunwensci.com):
摘要:用于飞机部件装配的机器人制孔加工是典型的离散孔群加工,为了提高飞机装配机器人制孔效率与制孔质量,研究了飞机装配机器人制孔的路径规划问题。首先,将某型号飞机矩形翼三维模型利用CATIA软件建立并提取制孔的点位信息;然后,对传统蚁群算法进行了改进,提出基于随时间改变的信息素挥发因子更新机制的优化蚁群算法,并将改进的蚁群算法与人工免疫算法相融合,形成优化免疫蚁群算法。仿真实验结果表明,改进的优化免疫蚁群算法的路径长度与传统蚁群算法相比缩短了接近20%,提高了算法的寻优能力和生成路径的质量,减少了算法的收敛时间,与传统蚁群算法相比迭代次数缩减了大约34%,有效提高了机器人制孔的效率。
关键词:CATIA软件;蚁群算法;信息素挥发因子;免疫算法;优化路径;优化免疫算法
Research and Implementation of Hole Making Path Planning and Algorithms for Upper Aircraft Assembly Robots
Liu Yanmei,Lyu Di
(School of Automation,Shenyang Aerospace University,Shenyang 110136,China)
Abstract:Robot hole making for aircraft component assembly is a typical discrete hole group processing.In order to improve the hole making efficiency and quality of aircraft assembly robot,the optimal path algorithm of hole making by aircraft assembly robots was studied.Firstly,the 3D model of a rectangular wing of an aircraft model was created using CATIA software and the point location information of the hole making was extracted.Then,based on the traditional ant colony algorithm,the pheromone volatile factor update mechanism with time was proposed to study the optimized ant colony algorithm,and the characteristics of the traditional ant colony algorithm and the artificial immune algorithm were analyzed and compared to form the optimized immune ant colony algorithm.The simulation results show that the path length of the improved immune ant colony algorithm is reduced by nearly 20%compared to the traditional ant colony algorithm,which improves the optimisation ability and the quality of the generated paths,the convergence time of the algorithm is shortened and the number of iterations is reduced by about 34%compared to the traditional ant colony algorithm,which effectively improves the efficiency of robot hole drilling.
Key words:CATIA software;ant colony algorithm;pheromone volatility factor;immunity algorithm;optimization path;optimization immunity algorithm
0引言
随着工业4.0的到来,航空领域迎来了新的挑战。现代飞机日渐复杂,对其性能、安全性、经济性都提出了更高的要求。飞机制造商要在满足高质量的前提下,去考虑客户的经济承担能力,这就促使提高生产效率成为当下飞机制造的重要议题[1]。影响飞机服役时间长短主要是装配连接的质量[2]。根据资料统计,70%的飞机疲劳事故来自于结构连接的部分,其中近3/4是由于连接孔的疲劳而断裂,所以提高制孔的质量与效率是飞机生产的关键[3]。国外自动制孔技术相对比较成熟,如美国的GEMCOR和英国的DELCAM等公司,拥有自主知识产权的飞机装配自动钻铆系统[4]。目前国内飞机制造领域,对于自动制孔技术的研究还处于发展阶段,对于自动制孔的路径规划算法的研究国内学者已取得诸多研究成果。
蚁群算法是解决路径规划问题的常用算法,是一种通过模仿自然界中的蚂蚁产生的智能群算法,其最大特点是具有正反馈特性[5]。然而,传统的蚁群算法仍然存在收敛时间长、容易产生陷入局部最优解的现象[6]。为了解决上述缺陷,许多学者纷纷提出了改进传统蚁群算法的思路。杨立玮等[7]通过初始信息素阶梯分配原则,解决了蚁群早期搜索的盲目性问题。按优化目标重构多因子信息素更新方式,并运用最大最小蚂蚁系统和自适应策略提高了全局搜索能力,规避了坠入局部最优的局面;沈葭栎等[8]开发了一种改进蚁群算法,依靠对信息素浓度进行动态分级设置,使信息素浓度在迭代过程中缓缓减少,成功地令算法收敛速度得到提升,当陷入局部最优解的情况发生时,加入了惩罚系数的概念来调节目前最优路径中信息素的浓度,提高了算法的全局搜索能力,增强了算法随机性;石立新等[9]本着保证路径长度的原则,将转向次数这一因素加入到启发函数中,与此同时限制了信息素变化的范围,增加了算法搜索空间的大小,使算法收敛到局部最优解需要的时间变长。
蚁群算法在前期由于信息素不足,执行周期比较长,免疫算法则正好相反,算法早期搜索速度快,但是当迭代进行了一定次数之后由于缺少反馈,算法进化速度骤然下降[10]。针对上述问题,本文提出一种动态优化信息素挥发因子,改善了传统蚁群算法的盲目性,并在传统蚁群算法的基础上引入免疫算法,提出优化免疫蚁群算法,以改善蚁群算法在初始搜索阶段收敛所花费的时间过长、易于陷入局部最优解等缺陷。此算法对提升飞机装配机器人自动制孔效率具有重要意义。
1基本原理
1.1传统蚁群算法
蚁群算法是根据生物界中的蚂蚁创造出来的一种仿生启发式算法,并带有正反馈特性[11]。在现实生活中,蚂蚁在移动时会同时释放出一种生物信息素,这种信息素像水一样,在自然状态下会随着时间的流逝而慢慢蒸发消失。因此,信息素含量在不同路径上会有明显的差别。蚂蚁爬行的路径长度越短,其所爬行的路径上存在的信息素含量就越高,路径长度越长,因为挥发现象的存在,其路径上的信息素保留的就会越少,因此,信息素含量高的路径被之后的蚂蚁选择的概率就相对大上许多,继续释放信息素加强了这条路径上信息素的含量[12]。蚂蚁们就是根据这样正反馈的方式,总能寻找出一条最短的路径。
当迭代进行到第t次时,k蚂蚁从孔位i点爬行到孔位j点的转移概率为p,其表达式为:
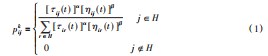
式中:k为蚂蚁的标号;下标前一位为当前位置,后一位为将要爬行到的位置,τij为t时刻孔i到孔j之间路径上的信息素浓度;ηij(t)为由孔i爬到孔j的期望程度,是i到j路径上的启发函数,其值与时间无关,ηij=1/dij,dij为孔i和孔j之间的欧式距离;H为蚂蚁可爬行的孔位信息的集合。
在迭代过程中,信息素更新规则如下:

其中信息素挥发系数为ρ(0≤ρ≤1),其功能是控制信息素的挥发程度的快慢。Δτ(t)表示第k只蚂蚁t时刻在孔i与孔j之间的路径上残留的信息素增量,它的大小与所选的蚁群算法的模型有关系,本文采用的是蚁周模型,故其公式为:

式中:Q为信息素强弱程度;Lk为蚂蚁k所爬行的路径的距离。蚁群算法的具体步骤如下:
(1)设置初始参数及环境,包括确定参数值蚂蚁循环次数N、蚂蚁数量M、初始时刻的信息素常数τc、信息素挥发系数ρ、边(i,j)的信息素轨迹强度τij的相对重要性α、蚂蚁到达目标点所释放的信息素总量Q、边(i,j)能见度ηij的相对重要性β等有关参数;
(2)根据蚂蚁的状态转移概率、环境模型及初始参数信息,完成从起始点到目标点的路径搜索,比较并记录M只蚂蚁的最短路径,以这条最短路径完成一次信息素的全局更新;
(3)继续步骤(2),直到达到蚂蚁的最大循环次数N。输出N次循环中的最短路径及路径长度,即为所求的从起始点到目标点的最短路径,结束。
1.2优化蚁群算法
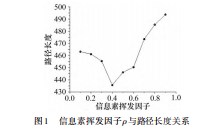
蚁群之间,蚂蚁和环境之间的交流依靠信息素,所以蚁群算法的关键也在于信息素的更迭。在算法中,信息素挥发因子ρ直接影响着信息素挥发的速度,所以蚁群算法的收敛速度很大程度上是被信息素挥发因子所决定的。传统的蚁算法在搜寻最优路径时需要依靠多只蚂蚁进行多次迭代,在进行处理大规模数据的模型时,蚂蚁在搜索路径的时候信息素不断挥发直至0,令某些路径不再被搜索,导致少数路径从没被搜索或很少被搜索,严重影响着算法的搜索能力。传统蚁群算法的信息素挥发因子ρ的初始取值范围为0~1之间,初始ρ值不同最后得到的最优路径就会不一样。所以本文应用TSP常用的数据库中的eil51,对ρ的初始值从0.1~0.9进行了试验,得到的路径结果如图1所示。由图和实际算法运行中发现,ρ大于0.6之后的路径结果不是很理想,甚至有时会出现算法崩溃的现象,这是因为当ρ过大时蚁群算法会陷入局部最优解,无法完成全局搜索,故无法得到路径长度;在ρ取0.1~0.3之间时,得到的路径长度也不是尽如人意;在ρ取0.3~0.6之间比较理想,尤其是0.4时为435.722 9。综上所示,当ρ的初始值取0.4时可以使算法达到最优效果,即全局搜索效果最好。因此,本文提出一种为应对传统蚁群算法全局搜索时间长,改进全局搜索能力低,搜索多次无法达到理想结果的情况,提出了一种对信息素挥发因子ρ随时间而改变的方法,即对其限制在0.3~0.6之间。其表
达式为:

式(4)中t≠0,因为已经把初始(t=0)时ρ取值为0.4。这样就可以避免因为ρ过大,路径上留存的信息素挥发过于迅速,不同蚂蚁之间的交流变少,算法的收敛时间过长,甚至存在算法陷入局部最优的死循环中的风险;ρ过小,路径上就会留存一些长时间滞留的信息素,有机会多次搜寻到已经确定过的路径,从而降低了算法的随机性,使算法缺少多样性,降低了全局搜索能力。
2优化免疫蚁群算法
2.1传统免疫算法
工免疫算法是生命科学与工程数学相互碰撞产生的一种优秀的智能优化算法[13]。人工免疫算法是将人类(高等脊椎动物)的生物免疫系统作为理论原型的[14]。因此,生物免疫系统是免疫算法的最直接的来源。免疫算法是根据免疫系统来设计的,例如抗原识别、免疫调节、克隆变异、免疫记忆等,免疫算法的概念与基础理论被应用到算法计算中[15]。
传统人工免疫算法的一般流程如下。
(1)识别抗原:确定亲和度评价函数和抗体浓度函数和目标函数。
(2)初始抗体产生:随机产生一个初始抗体群(目标函数在约束条件下的任意一个可行解)。
(3)亲和力计算:计算抗体群中每一个抗体的亲和度值。
(4)产生记忆细胞:抗体根据亲和程度从小到大进行分类,从抗体中分离出亲和力最高的抗体形成新的抗体群,选取前5%的亲和度较高的抗体形成记忆库。
(5)对于抗体的促进和抑制:计算抗体的浓度。促进低浓度高亲和力的抗体;抑制高浓度亲和力低的抗体。
(6)群体更新:利用交叉、变异等操作对群体进行更新。
(7)条件判断:判断是否满足终止要求,即达到规定迭代次数到达最大值或找到最优质的解,是则结束迭代,否则跳转到第(3)步。
2.2优化免疫蚁群算法
人工免疫算法和蚁群算法都属于智能集群算法。细胞之间、蚂蚁之间都进行着相互交流,单独的每个个体都和环境也都存在着交流影响,来更好地适应环境的变化。两种算法既有相似又有不同。人工免疫算法具有快速随机搜索的特点,但在算法运行后期信息利用不足,存在大量的繁琐的无效的迭代,算法效率不理想。蚁群算法具有并行搜索的特点,利用信息素的逐渐累积和迭代中不断更新信息素使算法渐渐收敛于最优路径,但其初次的信息素分布是随机产生的,易导致算法收敛速度慢。
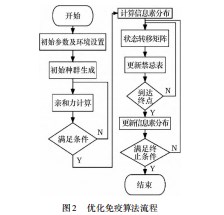
本文将人工免疫算法和优化蚁群算法相结合,提出一种优化免疫蚁群算法,算法主要分成3个部分,第一步利用免疫算法初期快速随机搜素的特点,首先对所求问题找一个较优可行解。其次通过得到的较优可行解对蚁群算法初始的(t=0)信息素分布进行生成。最后依靠优化蚁群算法的具有正反馈的特点和并行性来增强算法求解效率,并在算法迭代时应用上文提到的对信息素挥发因子的改进,得到最后所求的最优解。优化免疫蚁群算法的具体流程如图2所示。
具体步骤如下。
(1)确定抗原、抗体及初始参数和环境设置。
(2)生成初始种群。
(3)计算每个抗体的亲和力。
(4)抗体的促进和抑制:计算抗体的浓度。促进高亲和度低浓度的抗体;抑制低亲和度高浓度的抗体。
(5)群体更新:利用交叉、变异等操作对群体进行更新。
(6)输出可行解,若满足条件,执行步骤(7),若不满足,回到步骤(2)。
(7)生成蚁群算法的初始信息素的分布。
(8)设定初始参数,并确定状态转移概率。
(9)更新信息素。
(10)若满足条件,输出最优解,完成搜索。若不满足条件,回到步骤(8)。
2.3蚁群算法与优化免疫蚁群算法仿真比较
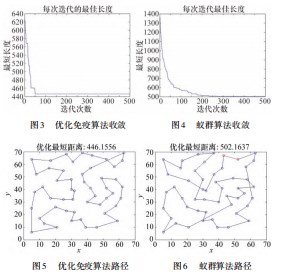
为验证本文的优化免疫算法的合理性,选择了国际上通用的测试库eil51分别对两种算法进行了仿真实验。通过对图3~4传统蚁群算法和优化免疫蚁群算法的收敛曲线仿真结果进行比较分析,优化免疫蚁群算法在迭代50次左右就已经收敛找到了最短路径,而传统的蚁群算法150~200次甚至更久才能找到该算法的最优解。由图5~6两种算法的路径图可以发现优化免疫算法的最短路径远远好于传统蚁群算法,为446.155 6,其图像中的交叉线段明显减少。由此可见,优化免疫蚁群算法的收敛速度要好于传统蚁群算法,找到的最优路径也比传统蚁群算法要等优秀。说明优化免疫蚁群算法改善了全局搜索能力和收敛速度慢的问题。
3机器人制孔路径规划仿真
为了验证优化免疫蚁群算法可以有效地应用在飞机制孔路径中,本文对飞机装配机器人制孔路径规划设计并实现了仿真实验。实验中选取的参数为:免疫算法部分:群体规模n=100,克隆个数10,交叉概率Pc=0.95,迭代次数G=500,变异概率Pm=0.02。优化蚁群算法部分:蚂蚁群体的个数m=100,启发式因子α=2,自启发式因子β=3,初始信息素挥发常数ρ=0.4,常数Q=1,迭代次数NC=500。本文首先在CATIA软件下建立某型号飞机的矩形翼模型,因本文提取的制孔点位信息在矩形翼的曲面上又对其孔位信息进行了提取,如图7所示。应用所提出的优化免疫蚁群算法设计路径规划,并利用MATLAB进行仿真实现。试验结果如图8所示,为简化仿真本文选取了一个长方体x=[0,500],y=[0,100],z=[-20,20]的空间为实验区间。仿真结果表明优化免疫蚁群算法可以应用在飞机零部件制孔当中,找到的制孔路径长度为1 350,是飞机装配机器人制孔所能找到的最优最短路径。
4结束语
本文应用CATIA软件对某型号飞机的矩形翼进行建模。针对飞机装配机器人制孔路径规划问题,设计了优化免疫蚁群算法,其核心是将免疫算法与蚁群算法相结合并适当地对搜索过程中信息素挥发因子ρ进行改变,对于传统蚁群算法的收敛速度进行了提升,并对全局搜寻最优值的能力进行了明显的加强。从客观上来看,减少了传统蚁群算法的收敛时间,提升了全局搜寻的能力等特点,说明传统蚁群算法的缺陷已经被优化蚁群算法所弥补,为飞机装配机器人制孔路径规划提供了基础理论与技术支持。利用仿真结果可以看出,设计的优化免疫蚁群算法,根据某型号飞机的矩形翼的制孔得到了一条最优路径来实现,并得到了较为理想的结果。
参考文献:
[1]杨阳,邱燕平,王晓宇.C919飞机装配自动钻铆技术的应用研究[J].教练机,2019(2):8.
[2]罗群,杨元,康永刚.电磁铆接技术在自动钻铆补铆中的应用研究[J].机械科学与技术,2016,35(1):6.
[3]林琳.民用飞机自动化装配制孔技术研究[D].上海:上海交通大学,2012.
[4]喻龙,章易镰,王宇晗,等.飞机自动钻铆技术研究现状及其关键技术[J].航空制造技术,2017(9):10.
[5]步燕芳.免疫蚁群算法及其应用[D].南京:南京理工大学,2009.
[6]武建华.基于移动节点路径规划的定位算法的研究[D].太原:太原理工大学,2012.
[7]杨立炜,付丽霞,郭宁,等.多因素改进蚁群算法的路径规划[J/OL].计算机集成制造系统:1-18[2021-12-30].http://kns.cnki.net/kcms/detail/11.5946.tp.20210723.1759.014.html.
[8]沈葭栎,李燕,季建楠,等.一种改进蚁群算法的移动机器人路径规划算法[J].现代计算机,2021(22):5.
[9]石立新.基于改进蚁群算法的机器人路径规划研究[J].航空计算技术,2021,51(2):28-31.
[10]肖艳秋,焦建强,乔东平,等.蚁群算法的基本原理及应用综述[J].轻工科技,2018(3):4.
[11]王洪元,卜莹,潘操.基于遗传蚁群算法的气田集输管网优化方法[J].计算机与应用化学,2012,29(12):4.
[12]王林林.一种新的无线传感网络路由算法的仿真设计与研究[J].赤峰学院学报(自然科学版),2016,32(5):32-35.
[13]吕岗.免疫算法及其应用研究[D].北京:中国矿业大学(北京),2003.
[14]王磊,肖人彬.基于免疫记忆的人工免疫算法模型及其应用[J].模式识别与人工智能,2002,15(4):385-391.
[15]舒万能.人工免疫算法的优化及其关键问题研究[D].武汉:武汉大学,2013.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/49407.html