SCI论文(www.lunwensci.com):
摘要:实变函数是数学师范类本科专业开设的一门重要专业基础课,它与先修课程数学分析中的很多概念和结论都存在紧密联系。在授课过程中将实变函数中的新概念和结论与数学分析中已知的一些概念和结论联系起来有助于提高实变函数的教学效果。本文结合笔者在实变函数课程教学过程中的体会,对该课程的教学方法进行了探讨。
关键词:实变函数;数学分析;教学方法
本文引用格式:李丹,等.实变函数课程的教学方法浅析[J].教育现代化,2019,6(24):187-188,218.
实变函数课是数学师范类本科专业的一门专业基础课。它不仅是数学分析课中微积分部分的继续、深化和拓展,也是泛函分析、偏微分方程、概率论与随机过程等后续课程的重要基础。与先修课程《数学分析》相比,该课程采用了截然不同的处理方法,并且需要漫长严密的准备铺垫,从而使学生对该课程感到很抽象、难懂。事实上,实变函数中那些表面上看似抽象、陌生的概念和结论,都与学生的已有知识有着密切的联系。在授课过程中,让学生以一种探究者的身份去学习和思考,并引导学生将实变函数中的新概念和结论与数学分析中已知的一些概念和结论进行对比分析,不仅能使学生把实变函数中那些新的概念和结论掌握的更好,而且还有助于培养学生的数学思想方法。为了达到这一目的,本文将从如下四个方面来谈谈笔者在实变函数教学中的点滴体会。
一 讲好第一堂课,加强学生对课程的整体把握
实变函数课的内容是自成体系,其处理方法与先修课程《数学分析》相比截然不同。特别地,它的精华部分需要前面好几章内容的严密准备。[1]这些特点使得实变函数的第一堂课成为学生学好这门课的重要基础,这就要求教师要认真备课,组织好教学内容。在第一堂课里,教师可以先从这门课与数学分析的联系出发,引出学习这门课的必要性,然后再引导学生探讨为什么要将这门课划分为好几个章节以及它们之间有什么联系,最后再简单介绍一下这门课与后续课程的联系,并从中强调学生学习这门课的重要性。
我们可以这样来设计实变函数课程的第一堂课。首先,教师引导学生一起回顾数学分析中黎曼积分的定义及其可积的条件。然后,通过下面两个例子指出黎曼积分的不足之处:[2]
例 1. 闭区间 [0,1] 上的狄利克雷函数

通过例1可以看出,对于仅取两个函数值的非常简单的狄利克雷函数,黎曼积分却不存在,说明黎曼积分所研究的函数空间的范围非常狭小。而例2表明,正是因为这种研究对象的狭小,使得黎曼可积函数列在极限运算下不具有封闭性,从而使得要想在黎曼积分意义下让极限运算和积分运算交换次序,就必须加上很强而且难于验证的条件,即函数列满足一致收敛性。教师和学生对这两个例子的探讨,能够激发学生想解决问题的好奇心、想进一步知道如何才能将黎曼积分所研究的函数对象的范围扩大,从而克服上面例子中出现的问题。这样以来,学生可以很自然地感受到建立新的积分(实变函数课程中的勒贝格积分)的必要性。
基于这些准备,教师可以用“计算一堆钞票总面值”的例子作为突破口,引导学生通过类比的方法很自然地想到:计算曲边梯形的面积可以用两种不同的方法,一种方法是用定义域分割曲边梯形, 即数学分析课程中的黎曼积分,而另一种方法是用函数的值域来分割曲边梯形,即实变函数课程中新的积分—勒贝格积分。[3] 这种借助于学生在日常生活中非常熟知的事情自然引出勒贝格积分所蕴含的崭新的积分思想的教学方法,能够让学生贴切地体会到即将学习的勒贝格积分事实上是来源于日常生活,从而让他们不会感到抽象和晦涩。
接着,教师将勒贝格积分思想中分割函数的值域的方法运用于例 1 中 [0,1] 上定义的狄利克雷函数D(x),学生会很快发现:与函数值 1 对应的自变量 x的范围 还没有定义“长度”,那么它的“长度” 又如何来定义呢?为此,要定义勒贝格积分,首先要面临的问题就是要解决好将通常区间长度的概念进行推广的问题,这就是实变函数课程中“勒贝格测度”这一章节要解决的问题。解决完函数自变量的定义域子集的“长度”问题后,接下来就需要确定被积函数的范围。那么,如何合理地定义被积函数才能使新的被积函数范围比黎曼可积函数范围更为一般呢?新定义的被积函数与数学分析中的连续函数之间又有什么关系呢?这就是实变函数课程中“可测函数”这一章节要研究的问题。有了这些准备之后,就可以来定义勒贝格积分,并研究讨论它的性质了。在第一堂课里,教师通过这种自主探讨方法引导学生学习,有助于帮助学生从宏观上把握实变函数课程的整体知识结构、内容体系,为以后的学习培养了学习兴趣。
二 坚持由浅入深、由具体到一般的教学方法
实变函数课程中的很多看似抽象、陌生的概念和结论,都与学生已有的知识有着密切的联系。例如, 基数的概念与有限集合中元素的“个数”、勒贝格测度与通常区间长度的概念、可测函数的定义与连续函数的等价定义等等,它们中的前者都是后者的深化与推广。因此,教师在讲授实变函数时,对每一个细节尽可能地由浅入深、由具体到一般,由已知到未知,逐步地对学生加以引导,可以加深学生对实变函数中新概念的理解以提高教学效果。同时, 学生在学习这些新概念的过程中,还可能掌握好这种从特殊到一般、从具体到抽象的科学研究方法。
下面以可测函数的定义作为一个例子,来探讨如何应用由浅入深、由具体到一般的教学方法。绝大多数实变函数教材都是在没有任何背景引入的情况下直接给出可测函数的如下定义:[1] 设函数 f 的定 义 域 是 可 测 集 E , 若 对 任 何 实 数 , 集 合{x E : f ( x) } 是可测集,则称 f 是 E 上的可测函数。如果教师在讲授这部分内容时,也像教材那样没有任何引入铺垫而直接给出上述定义,学生会感觉可测函数这个概念特别的抽象而难于理解。注意到,可测函数是连续函数的拓展。因此,可测函数的定义中应该保留有连续函数所具有的本质性质。倘若教师在讲授可测函数定义时,首先与学生一起回顾数学分析中连续函数的定义,并一起讨论得知:连续函数可以等价地定义为使得开集的原像都是开集的函数;然后,学生运用类比的方法很自然地想到:若函数 f 是连续函数,则对任何实数 ,集合{x E : f ( x) } 是开集,从而是可测集;最后, 教师再由此引出可测函数的定义,这时学生对可测函数的定义理解起来就容易多了。
三 加强实变函数与数学分析的联系
实变函数是数学分析的进一步发展,它是人们在解决数学分析理论中一系列问题的过程中产生和发展起来的。实变函数课程中的许多结论要比数学分析中的结果更加精细。例如,在数学分析中极限运算与积分运算交换次序需要函数列满足一致收敛条件。需要一致收敛条件的目的是保证函数列的极限函数仍然是黎曼可积函数,然而这个条件在实际中很难验证。实变函数通过扩大被积函数的范围,从而将一致收敛条件替换为更为容易验证的条件。为了看清楚这一点,我们再来回过头看看例 2. 在这个例子中,容易验证函数列{ fn }n1 不满足一致收敛条件, 并且其极限函数 D( x) lim fn ( x) 不再具有黎曼可积性;然而,在实变函数中狄利克雷函数 D( x) 却是勒贝格可积函数,并且对任意 x [0,1] 和 n 1,有fn ( x) D( x) 1 ,从而利用实变函数中的控制收敛定理 [1] 可得知函数列{ fn }n1 的极限运算与积分运算可交换次序,即
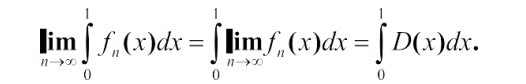
因此,教师在讲授实变函数课的过程中,如果能将实变函数与数学分析中相应的结论进行深入的对比,那么将会使学生对数学分析和实变函数内容都有更透彻的理解。
四 注重学生数学思想方法的教育
大多数学生毕业进入社会之后,在学校所学的数学知识可能很少能够直接用到,但是那些铭刻于头脑中的数学思想方法却一直影响着他们的生活和工作。在实变函数的教学过程中,教师有意识地加强对学生的数学思想方法的培养对学生今后的发展具有重要意义。[4]实变函数课程中的很多概念概括性和抽象性特别强,教师在教学中深挖和渗透数学思想方法,不仅能启发和培养学生的数学意识和数学思想,也能促进学生对知识的学习和领悟。
例如,实变函数中有两个重要的方法论意义的结论:[1]1.每一个非负可测函数可用一列非负单增的简单函数来逼近;2.可测函数可以用连续函数来逼近(鲁金定理)。基于这两个结论,实变函数课程中勒贝格积分的定义以及很多定理的证明都可以采用由特殊到一般的数学思想方法,即为证明某个结论正确,可以先证明它对简单函数或连续函数成立,然后再利用逼近的方法证明它对一般的可测函数也成立。例如,在定义勒贝格积分时,可以先定义简单函数的勒贝格积分,然后再运用上述的结论1由简单函数的积分逼近来定义非负可测函数的勒贝格积分,最后再将一般可测函数的勒贝格积分定义为两个非负可测函数的积分之差。在讲授实变函数时,如果对学生反复强调这种由特殊到一般的数学思想方法的重要性,那么学生在学习相关概念和定理的证明时就会感觉很自然,理解上不会有太多困难。同时,学生还可以通过实变函数这门课的学习,掌握好这种从特殊到一般的数学思想方法。
本文总结了笔者在实变函数教学中处理这些抽象内容时的点滴体会,其中仍有许多不足之处。在以后的教学实践过程中,笔者将对实变函数这门课程的教学方法进行进一步的研究与总结。
参考文献
[1]周性伟,孙文昌.实变函数[M].北京:科学出版社,2016.
[2]李会荣,周亚妮.实变函数课程教学方法研究与实践[J].当代教育实践与教学研究,2016,5:172-173.
[3]周性伟.讲授实变函数课的点滴体会[J].高等理科教育,2000,1:42-45.
[4]张力娜.数学思想方法与实变函数教学[J].价值工程,2012,10:203.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/9060.html