“教学评一体化”指导下的小学数学思维培养论文

 

　　关键词：小学数学,教学评一体化,思维,植树问题

 

　　“教学评一体化”指导下的小学数学教学对于学生理性的思辨，逻辑推理以及目标达成都具有积极意义。通过教师“教”，学生“学”，科学“评”学生会成为学习主体，通过思维主动探究的方式理解知识，找到解决问题的方法。教师要鼓励学生在探究中运用逻辑思考和推理判断的方式来进行，通过理性导航的方式得到客观的规律。学生主动参与到植树问题的探究中，成为学习主体，建构出知识框架和模型，形成系统性认识，在探究中从低效思考走向有序推理，实现思维活跃。学生在参与实践体验过程中会从不同角度探究问题，主动总结规律，通过思维活跃的方式来理解知识，提高思维品质。

 

 

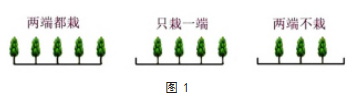
　　《小学数学课程标准》指出要解决问题教学必须从学生感兴趣的事物中提供观察和操作的机会，促进学生感受到数学知识的趣味性，实现学生快速解决问题。形象思维是一种非常直观的思维方式，它会给学生带来直观的印象，方便学生快速理解知识。在解决植树问题时，教师通过形象的方式带领学生画线段，会将抽象的数学知识直观化、形象化，启发学生的形象思维，帮助学生从直观的感知向推理判断转变，形成对知识的具体理解和认识。在探究“植树问题”时，教师可以让学生看到如下图形（图1），这样学生就会直观地看到什么叫做“两端都栽”“只栽一端”“两端不栽”。图形会给学生留下深刻印象，提高了教师语言表达的效果。在图形的帮助下，教师带领学生认识两端都栽树时需要注意“间隔数=总长÷间距”“总长=间距×间隔数”“棵树=间隔数+1”“间隔数=棵树-1”。有了图形的帮助，学生会直观地看到数学知识，融合教师语言的讲解和点拨会达到事半功倍的效果，促进学生快速理解知识，把握规律。

 

　　

 

 

　　在探究植树问题时，学生要借助于概念、判断、推理反映现实的知识，这个过程需要学生用科学去抽象概括，通过逻辑分析和推理判断的方式形成客观性认识，了解知识本质，形成主观性认识。学生从未知到已知的过程是一个循序渐进的过程，需要在判断中推理，在分析中归纳，形成对植树问题的科学认识。例如，在探究“植树问题”时，教师提供练习题，一条长为500米的公路，一侧架设电线杆，每隔50米架设一根，如果道路两端都不架设，一共需要多少根电线？通过学生对问题的思考，他们会认识到这个问题属于“两端不植树”的问题。在解决这一类问题时可以利用公路的总长度除以间隔的距离，求出一共有多少个间隔数。因为两端都不架设电线杆，需要在间隔数上减1。通过学生的一步步推理和分析，他们会找到解决问题的方法，形成主观性认识。在归纳总结中，学生也会通过逻辑思考的方式总结出这一类问题的通用公式，“总路程÷株距=间隔数”“间隔数-1=棵树”。逻辑思考会帮助学生更科学地了解知识的来龙去脉，促进学生思维品质的提升，实现数学学习能力的提高。

 

 

　　“教无定法，贵在有方”为了使学生理解植树问题方面的知识，教师要带领学生在解决问题过程中将遇到的困难和问题进行转化，改变原有的思考方向，朝着另一种方向挖掘和探究，会给学生带来不一样的灵感和启发，帮助学生找到解决问题的方法，在转化中间复杂问题简单化，帮助学生形成清晰思路。例如，数学中的锯木问题、方阵问题、爬楼梯问题等都可以转化为“植树问题”。在面对这一类试题时，教师要引导学生将题目中的信息转化为“植树问题”，寻找数学“原型”。例如，一个木工锯一根长19米的木条，他先把木头损坏部分锯下1米，然后锯了8次，锯成许多一样长的短木条。求每根短木条长多少米？解决问题时，学生会看到这是“植树问题”的一种转化。通过转化学生会把问题转化为植树问题，体会到数学知识的奥秘，认识到把现实中的具体问题转变成数学问题来解决，促进学生在转化过程中看到知识本质。通过思考学生会认识到木头截下损坏部分剩下18米，然后锯了8次说明这根木条被锯成8+1=9段，那么每根短木条长18÷9=2米。通过转化学生会了解知识本质，明确知识特征，更准确地找到数学信息，快速解决问题。

 

 

 

　　新课改强调学生是课堂主体。为了使学生理解植树问题，教师在课堂上要鼓励学生充分发挥主观能动性，引导学生自主学习，通过学生主动加工的方式内化知识。学生主动分析和判断会成为课堂主人，在思考中理解植树问题，内化知识。在解决问题过程中，计算是最基础的一步，教师要指导学生科学计算，准确计算，避免解题过程中出现问题。例如，面对问题，四年级共选49位同学参加校运会开幕式，他们排成一个方阵入场，这个方阵的最外层一共有多少人？分析中学生会用到所学的数学知识，49位同学排成一个方阵，每边应该是7人，因为7×7=49人。需要求最外层的人数，应该是7×4-4=24人。解题过程中学生会理解这是“植树问题”的一种形式，同时需要考虑到每一排学生的重合问题。不仅要学会分析问题，同时还需要计算准确。为了确保学生正确答题，在分析问题时学生会客观思考，在计算过程中会认真细致，做到计算准确，提高计算思维能力。

 

 

　　在“教学评一体化”指导的植树问题探究中，学生要学会将问题分类处理，主动建构解题框架和模式，在大脑中形成解题模型。学生在将问题分类处理时会思维活跃，提高思维能力和解题能力，调动学生的积极性和主动性。教师要鼓励学生将问题分类处理，帮助学生建构解题模型，面对相似的问题学会轻松应对。通过学生对“植树问题”的分类统计会认识到问题包含了封闭路线和不封闭路线两大类。在封闭路线问题中包括了圆形环岛、正方形、三角形等封闭图形相关的问题，以及两端种树、一端种树、两端不种树的不封闭路线问题。另外还有锯木头问题、敲钟问题、方阵问题、爬楼梯问题以及火车过桥问题等。在分类总结中，学生会看到问题虽然不一样，但涉及的原理都是“植树问题”。例如在锯木头问题中，学生要认识到木头的段数=次数+1；次数=段数-1；总时间=每次时间×次数。在过桥问题中，总长=车身长+车间距×车间隔数+桥长。学生把这些规律分类总结会活跃思维，面对相关问题时可以信手拈来，快速解决问题。

 

 

　　在探究数学问题时要培养学生的空间建构能力，感受上下、左右、前后和里外等方位，并且在大脑中建构出一幅图像，进行空间构造。在思考植树问题时，学生就要在大脑中想象树木的位置，构建出空间位置，有利于学生明确各个数量关系，快速解题。学生建构出了空间思维，就会了解树木的具体位置，有利于学生思维活跃，快速解决问题。例如，试题王爷爷在承包的正方形鱼塘四周种上了树，池塘边长为60米，每隔5米种一棵，四个角上各种一棵，王爷爷买了50棵树苗够吗？阅读试题后，学生会进行空间想象，思考王爷爷池塘的样子，进行空间构造。想象中学生会用具体的数据来解决问题，建构空间模型。因为池塘的边长是60米，每隔5米种一棵树，而且四个角上都需要种树，也就是每边种树的数量为60÷5+1=13棵。一共有四个边，在重合部分还需要把重合的棵数减去，所以需要13×4-4=48棵。解题过程中学生有了空间概念，就会在大脑中构建空间图形，体会位置关系，实现学生思维能力的提高。

 

 

 

　　在对学生的学习评价过程中，教师要鼓励学生从不同角度思考问题，以创新的方法解决问题。教师要鼓励学生打破常规思维的界限，采用发散思维的方式来探究问题，寻找解决问题方法。学生以超常规的方法和视角去思考问题，会找到与众不同的问题解决方案，促进学生创新思维能力的提高。在对学生“植树问题”进行评价时，教师要鼓励学生总结知识规律，了解题型特点，同时要引导学生创新思考，想到不同的设问角度和视角，在实际解题中灵活应用知识，达到对问题的灵活应用。评价过程中教师要引导学生试题中并不是所有的试题都是从“植树”角度来出题，还可以从不同角度来设问，进行创新性探究。例如，拉松比赛全程约42千米。平均每3千米设置一处饮水服务点（起点不设终点设），全程一共有多少处这样的服务点？这也是“植树问题”的一种灵活应用，突出了知识在生活中的价值。教师科学评价和点拨会给学生思路，促进学生了解试题特点，找到解决问题的方法，活跃思维。

 

 

　　在学习评价过程中，教师要从学生的整体表现和整体解题来客观地评价学生，促进学生将知识串联起来，通过点、线、面的方式形成一张完整的知识网络图。通过教师完整的评价和点拨，学生会站到一定的高度看问题，了解知识的来龙去脉，把握知识本质，面对问题时可以轻松应对。评价过程中教师要帮助学生建立有关“植树问题”的整体框架和架构图，促进学生形成对知识的系统性认识，面对这一类问题都能够灵活应对，轻松解决。教师在评价过程中要让学生看到这一类问题通常考查两端都种求全长，两端都种求树的棵数，两端都种求间隔长度，只种一端求全长，只种一端求树的棵数，只种一端求间隔长度，两端都不种求树的棵数，两端都补种求间隔长度。教师引导学生系统化知识，了解这一类试题的特点，建构出整体框架和认识，会提高学生的学习能力，促进学生在探究中成为学习主体，实现思维品质的提高。

 

 

　　在“教学评一体化”教学中，教师的评价对学生来说是指路的明灯，引导学生思考方向，促进学生找到解决问题的方法。教师要鼓励学生在探究植树问题时根据知识间的相似性质去比较和分析，尤其是将陌生的知识和问题与熟悉的问题进行比较，在类比中发现知识共性，找到本质，实现学生解决问题能力的提高。学生主动类比和探究会了解解决一类问题的通性通法，建构出解题模型，提高思维能力。例如，教师为学生提供试题，圆形花坛直径是10米，在花坛的周用摆上花盆，每隔1.57米放一盆，一共可以放多少盆？解题过程中学生会认识到这是“植树问题”的一种练习。评价中教师可以组织学生通过类比的方式进行试题改编，加工中学生会想到，在一个长为48米，宽为35米的长方形池塘四周上栽树，已知长边上每6米种一棵树，宽边上每隔5米种一棵树，那么这个长方形池塘四周一共要栽多少棵树？都是根据周长来求间隔问题，而且都是封闭路线。学生在评价中会思维活跃，通过类比的方式探究问题，实现学习能力的提高。

 

 

　　总之，通过“教学评一体化”的小学数学教学，教师关注了学生在课堂上的主体地位，会引导学生积极参与到课堂探究过程中。通过教师科学的“教”，学生主动地“学”，多角度地“评”会活跃学生思维，促进学生积极探究，成为学习主体。学生思维的运转会在加工中理解知识，在处理中建构框架，形成对知识系统性认识，推进学生的全面发展。学生思维品质提高会更好地理解数学规律，在解题过程中灵活应用，提高学习能力，落实核心素养。