SCI论文(www.lunwensci.com):
摘要:针对操作系统、离散数学课程建设和教学中存在忽视课程知识的相互关系、计算思维能力培养等问题,本文从这两门课程知识的依赖关系、学习的融合以及教学的协同等方面对它们的内在关系进行了分析和探讨,并提出了一种基于计算思维的内在关系,包括课程知识的依赖关系、学习的融合模式和协同教学模式等。
关键词:操作系统;离散数学;计算思维;协同教学;知识依赖
本文引用格式:龙陈锋,等.操作系统与离散数学课程关系分析[J].教育现代化,2019,6(09):133-136.
操作系统在计算机系统中具有非常重要的地位,是整个系统的核心。操作系统课程系统地对操作系统的基本概念、设计原理和方法进行了全面的介绍,侧重于系统的处理器、存储器、文件系统、I/O设备和用户接口等原理的基础知识[1]。离散数学是计算机科学中基础理论的核心课程。离散数学课程分别从基本理论和应用两个方面讲解了数理逻辑、集合论、代数系统和布尔代数、图论等基本知识[2]。这两门课程是计算机科学与技术、数据科学与大数据技术、物联网工程、智能科学与技术等专业的专业基础理论课程,具有理论性、实践性和抽象性都很强的特点。
一问题提出
深化本科教育教学改革是落实国家教育“十三五”规划的具体行动。本科教育改革主要侧重改进专业培养方案,强化课程研发,加大对课程建设、教学改革的常态化投入。操作系统和离散数学作为计算机科学与技术专业等多个信息类专业的重要课程,各学校均非常重视这两门课程教学和建设工作。离散数学是描述计算机系统的形式化语言工具,操作系统从基础理论和基本原理阐述了计算机系统的资源管理。操作系统的基础理论和原理需要借助离散数学这种形式化工具来描述或定义,因此两者之间的联系密切。但是,独立授课造成各自授课教师并没有针对课程内容进行深入交流,无法从方法、原理、内容等方面分析两者之间的关系,课程的教与学相对脱节,教学和建设效果一直不能得到很好的改善,主要原因是存在以下问题:
一是忽视课程之间的相互联系。一直以来,针对这两门课程的教学改革研究的文献都是对课程进行独立研究,注重理论,局部改革。高校一般都将离散数学作为操作系统的前导课程,在大学一年级开设,教学过程中偏重理论知识介绍而忽略具体应用讲解,使大多数学生无法明白该课程在本专业的具体作用和地位,学习枯燥乏味,积极性低。操作系统课程涉及许多离散数学知识,但是由于离散数学课程学习乏力,基础差,知识出现结构性断裂,学习上难以对接,操作系统授课老师难度增大。原因是两门课程知识之间承上启下的关系没有引起重视,课程的关联内容没有有效整合,碎片化的关联知识未拟合,造成了课程之间的壁垒,使得课程学习脱节。
二是计算思维能力培养乏力。离散数学主要学习掌握处理离散结构的描述工具和方法,并提高以抽象思维和严格的逻辑推理能力为核心的计算思维能力,但是在操作系统授课过程中,发现大多数学生无法理解操作系统有关进程、线程、地址映射、内存扩充、I/O模型等抽象性比较强的理论知识。这说明学习数理逻辑、抽象代数、集合论、图论等课程知识过程中的计算思维能力有待进一步加强培养。
基于上述问题,本文以它们之间承上启下的计算思维关系为基础挖掘和展现两者知识的高度内在关联性,将两者紧密衔接形成知识学习的连贯性,并从学习的融合和授课的协同两方面推动两者知识的宽泛拓展和深度延伸,从而改善课程学习效果,提升课程质量。
二 基于计算思维的知识承上启下关系
计算思维是针对问题求解、系统设计以及人类行为理解等,运用计算机科学的基础概念进行一系列的思维活动[3]。离散数学到操作系统的课程学习是从研究离散量的结构及其相互关系的数学到如何对计算机软硬件资源进行管理和抽象的学习,课程知识跨度大,学习思维也是蛙式跳跃。这种从形式化描述语言过渡到对计算机软硬件资源进行管理和抽象的思维是一次数学到计算机的大跨越思维活动。掌握处理离散结构的描述工具和方法,提高抽象思维和严格的逻辑推理能力是学好操作系统课程知识的前提,也有助于学生掌握如何利用形式化描述语言对计算机各种资源进行抽象的方法。因此,两门课程存在一种基于计算思维的知识承上启下关系。
(一)知识的依赖关系
为了保证计算机系统运行的严密性、结果的可再现性、学科理论方法与实现技术的高度一致,计算机科学与技术学科必须与数学学科紧密联系在一起,以数学为其理论基础,特别是数学中以代数、逻辑为代表的离散数学[4]。要设计出性能好的操作系统,操作系统的逻辑基础与构造性数学的逻辑基础必须保持一致。因此,两门课程知识具有高度的依赖性。
(1)数理逻辑为操作系统具体实现提供了运算基础。数理逻辑作为离散数学课程中的重要内容,是用数学方法研究形式逻辑的一门学科,这里的数学方法主要是指引进一套符号体系的方法。即数理逻辑应用数学方法引进一套符号系统来研究思维的形式结构和规律,利用计算的方法来代替人们思维中的逻辑推理过程。数理逻辑的主要研究内容是证明论、模型论、递归论和公理化集合论,以命题逻辑和谓词逻辑为共同的基础。命题逻辑是研究命题通过逻辑联结词构成更复杂的命题并进行逻辑推理的方法和原理。谓词逻辑是研究除了含有常项以外还含有变项的逻辑公式之间的逻辑推理关系。
操作系统是一组能有效的组织和管理计算机软硬件资源,合理地对各类作业进行调度以及方便用户使用的程序集合。每个程序是一个内部嵌套一系列复杂的、逻辑缜密的组件构成,其实现蕴含许多的逻辑关系,以数理逻辑方法为基础。例如:编程实现进程或作业先来先服务、高优先权、按时间片轮转调度算法实验时,需要用到了逻辑联结词非“非”、“或”等。
(2)集合论为操作系统抽象实现提供了描述方法。集合论[5]是研究公理化集合论和抽象集合论的数学理论,提供了要如何描述数学物件的方法,主要包括集合、关系和函数等内容。集合是由各种不同元素构成并用统一的方法来处理的对象。操作系统中常用集合来描述一个对象,进程集合、资源类型集合等。例如,程序并发执行的条件——Bernstein条件可以用集合论抽象描述为:定义集合R(Pi)={a1,a2,a3,…,am}用以表示程序Pi在执行期间所需参考的所有变量的集合(称为“读集”),W(Pi)={b1,b2,b3,…,bn}用以表示程序Pi在执行期间所要改变的所有变量的集合(称为“写集”),两个程序并发执行且具有可再现性的条件当且仅当R(P1)∩W(P2)
∪R(P2)∩W(P1)∪W(P1)∩W(P2)={}。
关系是笛卡尔乘积的子集,描述了集合中的元素之间某种联系,主要分为二元关系、偏序关系、等价关系、相容关系等。函数是具有特殊性质的二元关系,能把一个有限集合变换成另外一个有限集合。即将一类中的每一个对象关联到另一类中唯一的一个对象,是一种特殊的关系,操作系统中的I/O(Input/Output,输入/输出)关系常常被当作这种函数。操作系统中一般用集合论来定义模型,例如操作系统中使用基于角色的访问控制RBAC96模型[6]的形式化定义为:
U:用户集
R和AR:R代表普通角色集,AR代表管理角色集,且两者交集为空;
P和AP:P代表普通权限集,AP代表管理权限集,且两者交集为空;
UA⊆U×(R∪AR):用户与管理角色之间的多对多对应关系;
PA⊆P×R:访问权限与角色的多对多关系;APA⊆AP×AR:管理权限与管理角色的多对多关系;
RH⊆R×R:存在偏序关系的普通角色级别;ARH⊆AR×AR:存在偏序关系的管理角色级别;
S:一个会话集;
user:S→U定义了一个会话si与单个用户user(si)之间的映射函数在本次会话的生存期内不会发生变化;
roles:S→2RUAR定义了一个会话si与角色集rol es(si) 之间的映射函数使si能获得授权 ;
这里有一组约束条件用来允许或禁止以上所提到的所有元素的值。这种形式化定义既体现了集合,又有关系和函数的运用,将操作系统中有关功能实现直接用离散数学知识抽象表达出来。
(3)代数系统为操作系统理论发展提供了研究方法。代数系统是指定义有若干运算的集合,代数系统与操作系统的并发、非确定性、资源访问、可信机制等联系非常紧密。随着硬件不断更新换代、计算机体系结构不断发展、新的应用需求出现等,推动了操作系统理论不断的创新和发展。为了更加清晰描述操作系统硬件到软件的抽象、部件功能的抽象、概念表达抽象等,国内外学者围绕操作系统广泛开展了的相关理论研究,先后对进程并发及非确定、计算机资源访问易泄密信息、调度可视化等问题进行深入研究,提出了进程并发模型[7,8]、含幺半群的资源访问模型[9]、通信共享资源的代数及并发系统性质[10,11]、基于格的访问控制模型[12]等成果,并用以代数系统为主的数学方法来进行严格的形式化规范说明。
(4)图论为操作系统易理解提供了表达方式。描述现实世界最有效的、最直观的工具就是图。图论是离散数学中非常重要的内容,由点和连接点的边组成。操作系统中往往用点表示一个对象,用边表示对象之间的关系,而且二元关系的系统,图论均可提供一种数学模型。操作系统中进程状态、进程同步、进程交互、进程调度、死锁、目录等都是以图论为基础进行形式化定义。在多道程序系统中,利用前趋图描述了进程、程序或语句的执行先后顺序关系。作为一个有向无环图,图中的每个结点用于描述一个程序段、某个进程或是一条程序语句等,结点间的有向边用于表示两个结点之间的先后顺序以及存在的偏序或前趋关系。死锁检测是系统利用资源分配图来描述,通过判断系统某一个状态的资源分配图能否可完全简化来实现。通用的操作系统普遍都采用了标准的树形目录结构,即将一个文件系统表示成树,其中根表示根目录,内点表示子目录,树叶表示文件或空目录。
计算机操作系统理论研究与实现中,描述同步问题的模型Petri网[13]、交互进程模型[14]、并发控制模型[15]等都是基于有向图来实现。
(二)学习的融合关系
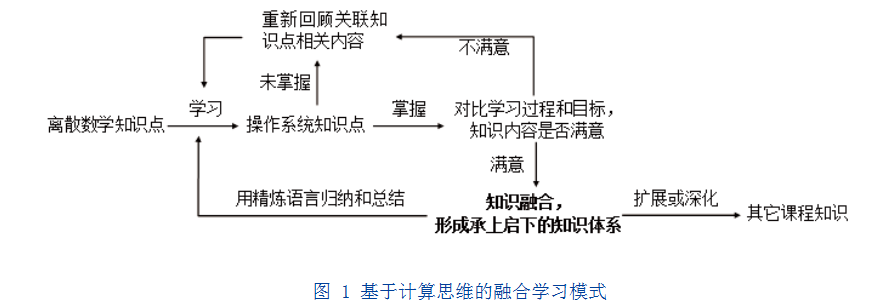
离散数学课程中的知识为操作系统课程学习提供了学习基础和计算思维训练,必须作为操作系统的先修课程,操作系统课程学习需要高度依赖离散数学的课程知识,学生才可能取得比较好的学习效果,将离散数学知识贯穿融合到操作系统课程中,从而将两者关联知识形成一条承上启下的课程知识体系链并扩展和融合到其他相关专业课程知识,如图2所示。离散数学依赖操作系统课程来检验课程知识的实践效果,将它们关联的知识基于计算思维进行深层次融合来推动和建设,进一步形成一个牢固的知识融合课程体系,更好得奠定本专业知识基础。同时,形成以操作系统课程为中心,纵向深入挖掘数据结构、计算机网络、编译原理、计算机体系结构等课程的融合关系,横向拓展延伸到C程序设计语言和汇编程序设计语言、Linux操作系统、Android程序设计等课程的融合关系,构建一个立体化的关联课程知识融合体系。在这个知识融合体系构建过程中,始终以培养学生的计算思维能力为主线,以这两门课程的知识脉络融合为路,使学生能够梳理、体验和完成一次完整的离散数学知识与操作系统知识相互之间的逻辑推演和抽象能力训练。
这两门课程知识融合是一次关于离散数学知识到计算机操作系统知识大相容。知识融合可促使学生将专业常规知识灵活甚至创造性的运用到不同的情景和实际问题并以此扩展自己的专业知识和能力。融合了离散数学和操作系统底层知识,既能增强了专业的数学“内涵”,又打通了专业知识的底层“脉络”,更好地培养了专业素养。
(三)授课的协同关系
同时,离散数学课程没有体现如何应用形式化的离操作系统和离散数学彼此独立开课,相互之间的依赖、思维模式及学习要求融合在一起形成了授课顾此失彼的局面。学生掌握的离散数学知识不能达到操作系统课程学习的要求,需要重新讲述旧知识;散数学知识描述操作系统相关原理或方法,给学生学习带来了一定的困惑,往往不知道如何利用离散数学知识来描述操作系统模型及相关功能等内容而陷入某种疑惑中。
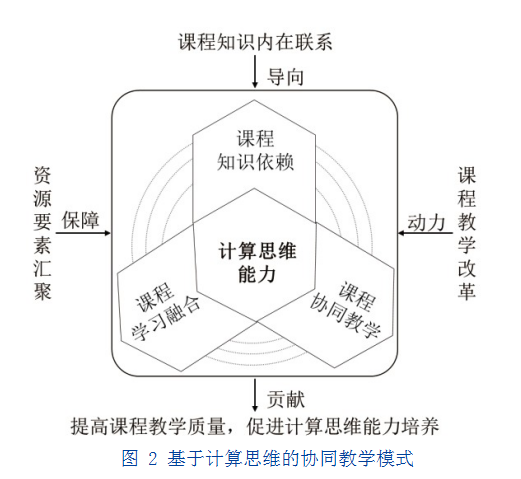
了解决上述问题,基于课程知识的依赖性和学习的融合性,围绕改善课程教学效果和培养计算思维能力为主线,以课程质量建设为源动力,整合相关课程资源和师资,系统思考与科学统筹,破除课程之间的障碍,将这两门课程的关联知识有效融合,实现授课与学习的良性互动,构建一种基于计算思维的课程协同教学模式,如图2所示。这种模式围绕教师备课、教学组织、教学方法和方式等进行全方位的协同设计,通过两者协同教学,将两门课程知识辅以教学方法创新、教学策略创新及知识体验创新的有机衔接,形成这两门课程教与学的计算思维,使两门课程知识深度融合、彻底理解和真正领悟,促进学生对它们的认识,厘清之间的关系。
三 结束语
本文详尽分析了这两门课程之间的知识关联性,总结出了它们的相互关系,将它们深度融合,特别是运用离散数学知识对操作系统的原理、功能、模型等进行形式化的描述或定义,以便教与学更加通俗易懂。涉及到两门课程关联的知识,授课必须讲透它们之间的依赖关系和学习的融合关系。教学实践证明分析清楚这两门课程的关系,开辟了一种新的课程教学方式,探索了一种新的课程学习方法,使学生能够以另一种视野去学习离散数学和操作系统课程,更好的掌握了抽象性描述是如何实现和定义的方法。但是本文仅选择了两者之间几个比较明显的关系进行了分析,其深层次的关系需要进一步研究和挖掘,尤其是关联知识需要更层次的梳理和挖掘。
参考文献
[1]William Stallings.Operating Systems:Internals and Design Principles(9th Edition)[M].New York:Pearson Education Limited,2017.
[2]Kenneth H.Rosen.Discrete Mathematics and Its Applications(7th Edition)[M].New York:McGraw-Hill Education Inc.,2011.
[3]Jeannette M.Wing.Computational thinking[J].Communications of the ACM,2006,49(3):33-35.
[4]致琢,刘椿年,许满武,等.计算机科学与技术一级学科面向21世纪系列教材一体化建设研究报告[J].计算机科学,2002,29(06):33-46+110.
[5]方世昌.离散数学(第三版)[M].西安:西安电子科技大学出版社,2017.
[6]Ravi Sandhu.Rationale for the RBAC96 Family of Access Control Models[J].In Proceedings of the 1st ACM Workshop on Role-Based Access Control,page 9,New York,NY,USA,1996.ACM Press.
[7]G Milne,R Milner.Concurrent Processes and Their Syntax[J].Journal of the Acm,1979,26(2):302-321.
[8]Carl Adam Petri.Concurrency Theory.Lecture Notes in Computer Science,Vol.254 Proceedings of an Advanced Course on Petri Nets:Central Models and Their Properties,Advances in Petri Nets 1986-Part I.
[9]David Pym,Chris Tofts.A Calculus and logic of resources and processes.Formal Aspects of Computing,2006,18(4):495–517.
[10]I Lee,P Bremond-Gregoire,R Gerber.A process algebraic approach to the specification and analysis of resource-bound real-time systems[J].Proceedings of the IEEE,1993,82(1):158-171.
[11]Insup Lee,Anna Philippou,Oleg Sokolsky.Resources in process algebra[J].The Journal of Logic&Algebraic Programming,2007,72(1):98-122.
[12]Ravi S.Sandhu.Lattice-based access control models[J].Computer,1993,26(11):9-19.
[13]T.Agerwala.Towards a theory for the analysis and synthesis of systems exhibiting concurrency[D].Baltimore:Johns Hopkins University,1975.
[14]Glen Newton.Proving properties of interacting processes[J].Acta Informatica,1975,4(2):117-126.
[15]Tada o M ura t a.Pe t ri Ne t s:Prope rt i e s,Ana l y si s a nd Appllication[J].Proceedings of the IEEE,1989,77(4):541-580.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/7852.html