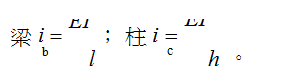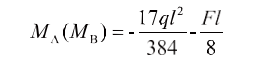SCI论文(www.lunwensci.com):
摘要:钢筋混凝土框架结构是目前各类建筑设计中运用最为广泛的结构形式。因此,框架结构也成为当前高等院校土木工程专业毕业设计中普遍采用的结构选型。根据毕业设计的任务要求,往往需要选取有代表性的横向一榀框架进行内力手算。在竖向荷载作用下的一榀框架内力计算时,由于结构布置方案的差异,可能会出现各种不同的荷载工况。论文以框架结构为例,讨论弯矩二次分配法中不同荷载工况下梁固端弯矩的求解及易出现的错误。
关键词:土木工程;框架结构;弯矩二次分配法;荷载工况;固端弯矩
本文引用格式:蒋建华,等.土木工程毕业设计弯矩二次分配法中固端弯矩的求解问题[J].教育现代化,2019,6(05):139-142.
钢筋混凝土框架结构是目前各类建筑物设计中运用最为广泛的结构形式。因此,框架结构也成为当前高等院校土木工程专业毕业设计中普遍采用的结构选型[1]。为了让学生更好的掌握结构设计计算的全过程,毕业设计大都采取手算和电算相结合的方式完成。根据毕业设计的任务要求,往往需要选取有代表性的横向一榀框架进行内力手算。在竖向荷载作用下的一榀框架内力计算时,由于结构布置方案的差异,可能会出现各种不同的荷载工况。学生在完成这部分内容时,经常会遇到困难,容易发生错误,尤其是面对较复杂的荷载工况。鉴于此,论文以框架结构为例,讨论弯矩二次分配法中不同荷载工况下梁固端弯矩的求解及易出现的错误。
一 弯矩二次分配法基本步骤
多层多跨框架在竖向荷载作用下,侧移很小,各层荷载对其他层杆件的内力影响不大,可采用弯矩二次分配法计算结构内力。弯矩二次分配法是在满足工程计算精确度的条件下,对力矩分配法计算过程进行简化[2]。计算过程中,框架不必分层,整体计算,所有节点同时分配力矩,又同时向远端传递,再将节点的不平衡弯矩再分配一次即完成。这种方法适合于手算。
弯矩二次分配法的计算要点如下[2]:
①计算梁柱的线刚度,即:
② 计算各杆端的固端弯矩和弯矩分配系数,计算弯矩分配系数时,柱的线刚度不折减;
③ 将所有节点的不平衡弯矩同时反号分配 ( 第一次分配);
④将各杆端的分配弯矩乘以传递系数同时向远端传递(第一次传递);
⑤将各节点传递弯矩同时反号分配(第二次分配);
⑥将各杆端的固端弯矩、分配弯矩、传递弯矩叠加,即为各个杆端的最终弯矩。
二 固端弯矩的求解
计算单元确定以后,根据板的导荷方式得到梁上的荷载分布,作出计算简图以求解固端弯矩。固端弯矩是节点不平衡弯矩的一部分,固端弯矩的求解是弯矩分配法计算的关键步骤,因而显得至关重要。
进行手算时,固端弯矩可根据荷载工况利用结构力学知识求解。一般地,固端弯矩的求解可分为以下两种计算情况:一是框架梁上满布梯形或三角形荷载;二是结构布置时在框架梁上设置次梁形成了更复杂的荷载分布。
毕业设计中常见的荷载工况主要有以下五种,下面针对每一种工况进行讨论并给出固端弯矩的计算公式。每种工况计算时均不考虑梁自重。
(一)工况一
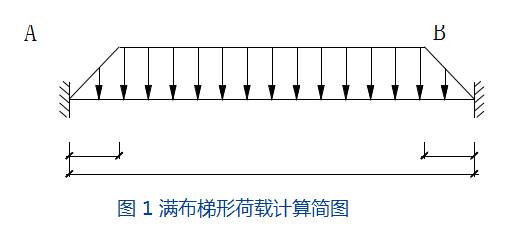
当所选框架梁AB上无次梁,且梁两侧均为双向板时,得到如图1所示的满布梯形荷载。
此时,可根据固端弯矩相等的原则将梯形荷载F等效为均布荷载 [3,4]:
(二) 工况二
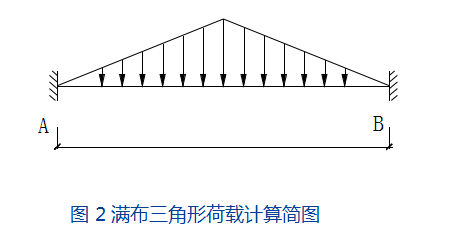
当框架梁 AB 上无次梁,且 AB 为双向板的短边时,得到图 2 所示的满布三角形荷载。
(三) 工况三
当框架梁 AB 跨中有一道次梁,且 AB 之间均为双向板的短边,形成如图 3 所示的荷载工况。
此时,AB梁上作用有两个三角形荷载和一个集中荷载,可采用叠加法进行固端弯矩的求解。首先,根据固端弯矩等效的原则将三角形荷载等效为均布荷载(不考虑F),等效公式如下:
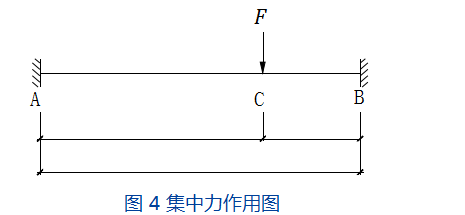
考虑集中荷载 F 单独作用时的一般工况如图 4 所示。此时固端弯矩大小为 [5]:
在 工 况 三 中, 集 中 荷 载 位 于 跨 正 中, 即d=e=l/2,两端弯矩相等,代入式(6)得到集中力产生的端弯矩大小为 -Fl/8。于是,梁 AB 的固端弯矩即为等效均布荷载产生的固端弯矩与集中力产生的固端弯矩之和,即:
在工况三的计算中,大家容易发生的错误是仍利用公式(3)来等效三角形荷载,从而影响计算的准确性。
(四)工况四
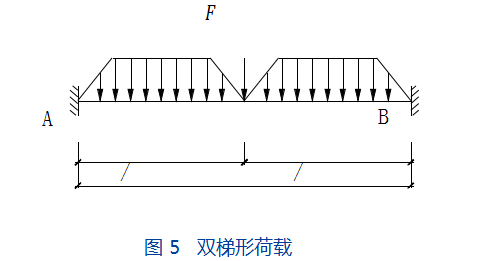
当框架梁AB跨中有一道次梁且AB之间均为双向板的长边,形成图5所示的荷载工况。
此时,AB梁上作用有两个梯形荷载和一个集中荷载。采用叠加法计算,细分为以下三种荷载情况:满布梯形荷载(图6所示)
同工况一,可利用公式(2)求得MA1。
2.跨中集中荷载
同工况三中的集中力作用,可利用公式(6)求得MA2。
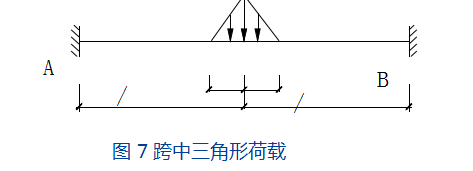
3.跨中三角形荷载(图7所示)
(五) 工况五
当框架梁上靠近支座一侧有次梁,且梁上既有双向板长边传递的荷载又有另一双向板短边传递来的荷载时,形成图 8 所示荷载工况。
手算时,仍可采用叠加法求解固端弯矩。将图 8 中梁左端的梯形荷载分解为一个均布荷载(图 9) 和两个小三角形荷载(图 10、图 11);梁右端的三角形荷载分解为两个小三角形荷载(图 12、图 13)。具体计算过程如下:
1.集中力作用利用公式(6)求得固端弯矩 MA1、MB1,其中d=2a+c,e=2b。部分均布荷载作用(图 9 所示)
三 结语
土木工程专业毕业设计中,由于不同建筑物的实际需求,在建筑设计方案的基础上会形成不同的结构布置方案,进而在结构内力计算时会遇到各种荷载工况。通过本文的讨论计算可以看出,进行手算时,对称的结构布置方案的固端弯矩计算要比非对称的结构布置更加简便。本文给出了毕业设计中常见荷载工况下的梁固端弯矩计算方法,可以为土木工程专业学生在毕业设计中提供参考,避免发生错误。
参考文献
[1]罗若帆,王莺歌,王仕成.土木工程毕业设计常见问题探讨与分析[J].广东水利电力职业技术学院学报,2016,14(4):27-31.
[2]郭靳时,金菊顺,庄新玲.钢筋混凝土结构设计[M].武汉:武汉大学出版社,2013.
[3]张仲先.土木工程专业毕业设计指南——混凝土多层框架结构设计[M].北京:中国建筑工业出版社,2012.
[4]东南大学,同济大学,天津大学.混凝土结构(中册)混凝土结构与砌体结构设计第六版[M].北京:中国建筑工业出版社,2016.
[5]朱星彬,侯丰泽.等截面杆件固端弯矩的简化计算方法[J].建筑技术开发,2004,31(4):11-12.
[6]浙江大学.建筑结构静力计算实用手册[M].北京:中国建筑工业出版社,2009.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/7722.html