SCI论文(www.lunwensci.com):
摘 要:分类讨论是数学学科的重要思想之一,每年高考题都会涉及到分类讨论思想的考查, 是高中数学教学的重点.为提高学生的分类讨论思想能力,促进其解题能力及数学学习成绩的提 升,教学实践中应采用理论讲解和习题巩固相结合的教学方法,指导学生在不同题型中的应用分类讨论思想.
关键词:分类讨论思想;高中数学;解题
分类讨论思想在高中数学解题中有着广泛的应 用,不同习题分类讨论的切入点及讨论标准存在差 异,因此,教学实践中应为学生做好解题示范,注意 预留“空白”,要求学生认真揣摩分类讨论的标准与 过程,做好方法的归纳、整理,以便理解与掌握分类 讨论法.
1 解答三角函数习题
三角函数题中产生分类讨论的情况主要有周 期、相位、图象的不确定等,解题时应从这些不确定 的对象入手,运用已知条件尽可能的将不确定对象 的范围进一步精确,通过分类讨论尝试推导出矛盾, 从而解决问题.
点评 根据函数f( x ) 在给定区间的单调性,确 定其周期范围,再运用周期公式得出 ω 的范围.结 合图象中的已知点、对称轴进行分类讨论,看计算出 的 ω 是否在解得的范围内,得出最终结果.
2 解答解三角形习题
解三角形 常 用 的 知 识 点 有 正 弦、余 弦 定 理 , 但在运算的过程中可能会出现多种情况 ,此时需 进行分类讨论.分类讨论的依据有三角形的内角 的分类 ,边的分类等.分类讨论中 ,若某种情况能 推出矛盾 ,则应舍去该种情况;如不能推出矛盾 , 则该种情况成立.
点评 根据题干中给出的等式,运用正弦定理 进行转化得出 cosA 的值有两个;分别对两个值讨 论,发现 cosA =


不符合题意,而 cosA =
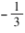
符合 题意,在 cosA =
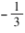
的条件下计算出△ABC 的面积即可.
3 解答导数习题
导数是高中数学中最易考查分类讨论思想的知 识 [1] . 分类讨论常出现对函数求导后,因参数值的 不确定性,导致函数在不同区间的单调性不同.对参 数分类讨论过程中,判断得出的参数值或范围是否 符合题意.
例 3 已知函数 f( x ) = xex + 1 , g( x ) = a ( ex -1) , 当 x > 0 时,有f( x ) ≥g( x ) , 则实数 a 能取到的 最大整数为( ) .
A. 1 B. 2 C. 3 D. 4
解析 令 h( x) =f( x ) - g( x ) = xex + 1 - a ( ex - 1) = ( x - a) ex + a + 1 , 则 h ′ ( x) = ( x - a + 1) ex .
当 a≤1 时,h ′ ( x) > 0 在(0 , + ∞ ) 上恒成立,此 时,h( x) 单调递增,要想满足题意只需 h(0) ≥0 , 此时 h(0) = 1 满足题意.
当 a > 1 时,令 h ′ ( x) = 0 , 解得 x = a - 1 , 则当 0< x < a - 1 时 h ′ ( x) < 0 ,h( x) 单调递减;当 x > a - 1时,h ′ ( x) > 0 , h( x ) 单调递增;h( x ) min = h( a - 1) =- e a - 1 + 1 + a , 要想满足题意只需 - e a - 1 + 1 + a≥0 ,即 1 + a≥e a - 1. 当 a = 2 时. 3 > e 成立;当 a = 3 时 4> e2 不成立.
综上分析,实数 a 能取到的最大整数为 2 , 故选 择 B 项.
点评 求参数 a 能取到的最大整数,需将问题 转化为恒成立问题,而恒成立对应求函数的最值,因 此,分类讨论主要围绕求函数的最值展开,期间需灵 活应用导数知识.
4 解答数列习题
数列习题中分类讨论常出现的情况有公差和公比的不确定性、通项公式的不确定性等,尤其对于部分数列需将偶数项与奇数项的通项公式分开考虑, 运算时应搞清楚奇、偶项的内在联系,保证推理的严 谨性与正确性.
例4 已知数列{ an }中 a 1 ∈Z,an +1 + an =2n +3,前 n 项的和为 Sn ,若 S13 =am ,则正整数 m =( ).
A.99 B.103 C.107 D.198
解析 由 a n + 1 + a n =2 n +3 得到 a n + 1 -( n + 1)-1 = -( a n - n - 1),则数列{ a n - n - 1}为公比 1的等比数列,则 a n - n - 1 =( - 1)n - 1( a 1 -2),由数列{ a n }前 n 项的和为 S n 得到:S 13 = a 1 +( a2 + a3 )+ … +( a 12 + a13 )= a 1 +2(2 +4 + … +12)+3 × 6 = a 1+102.
当 n 为奇数时 a 1 -2 + n + 1 = a 1 + 102,解得 m=103;当 n 为偶数时,-( a 1 -2)+ n + 1 = a 1 + 102,m=2 a 1 +99由 a 1 ∈Z ,则 m =2 a 1 +99 只能为奇数,此时无解.综上分析 m =103 ,选择 B 项.
点评 数列的的通项公式中含有( - 1)n - 1 ,导致数列的偶数项与奇数项的值不同,因此,需将其分 开进行考虑,推理、计算出符合题意的结果.
5 解答圆锥曲线习题
圆锥曲线是高中数学一个重难点,圆锥曲线习 题中产生分类讨论的情况多种多样,尤以直线与圆 锥曲线的关系不确定时为讨论的切入点,讨论过程 中为减少运算量,提高运算效率,应认真观察图形, 注重几何性质的应用.
例 5 已知 F1 ,F2 为双曲线 C:x2
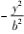
= 1( b >0)的左、右焦点,过点 F2 的直线和双曲线交于 A ,B 两点,当△ABF1 为等边三角形,则 b 的所有取值的 积为( ).
A .2 B .3 C.2 2 D.2 3
解析 (1)当过点 F2 的直线和双曲线相交的情境如图 1 时,设|AF2|= m( m > c - 1),则由双曲线定义可得|AF1|=|AF2|+2a = m +2,由△ABF1为等边三角形,可得|AF1|=|BF1|=|AB|= m +2,可得|BF2|=2,由双曲线的性质可得|BF1|-|BF2|=|AB|-|BF2|= m =2,则|AF2|=|BF2|,则 AB⊥F1 F2 ,则 2c =4 cos30 ° =2 3 ,则 c = 3 ,b = 2;
(2)当过点 F2 的直线和双曲线相交的情境如图 2 时,设|BF2|= n( n > c -1),则|BF1|=|BF2|+2 a = n +2,由△ABF1 为等边三角形,可得|AF1|=|BF1|=|AB|= n +2,|AF2|=2 n +2,又由|AF2|-|AF1|=2 n +2 -( n +2)=2,解得 n =2,则|AF1|=4,|AF2|=6,则△AF1 F2 中由余弦定理可得|F1 F2|2=|AF1|2 +|AF2|2 -2|AF1|AF2||cos60 ° =2 7 ,则 c= 7 ,此时,b = 6.结合以上两种情境可得 b 的所有取值的积为 2 × 6 =2 3 ,选择 D 项.
点评 对于情况一 ,等边△ABF1 位置较为特 殊 ,可借助双曲线和等边三角形性质构建线段之 间的关系 求 解.对 于 情 况 二 ,则 需 应 用 余 弦 定 理 进行运算.
综上所述,应用分类讨论思想解答数学题时,应 明确为何要进行分类讨论,分类讨论的依据是什么, 怎样对分类讨论的结果进行合理取舍,等[2].解题 教学中,为使学生掌握技巧、把握思路,既要展示经 典例题,又要加强专题训练,启发学生的同时,帮助 其积累丰富经验,增强应用能力.
参考文献:
[1] 俞洁.高中数学问题中的分类讨论思想例谈[ J].中学数学,2022(03):35 -36.
[2]顾宣峰.分类讨论思想在高中数学解题中的应 用[ J].高中数理化,2021( S1):20.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/76101.html





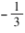 符合 题意,在 cosA =
符合 题意,在 cosA =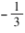 的条件下计算出△ABC 的面积即可.
的条件下计算出△ABC 的面积即可.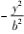 = 1( b >0)的左、右焦点,过点 F2 的直线和双曲线交于 A ,B 两点,当△ABF1 为等边三角形,则 b 的所有取值的 积为( ).
= 1( b >0)的左、右焦点,过点 F2 的直线和双曲线交于 A ,B 两点,当△ABF1 为等边三角形,则 b 的所有取值的 积为( ).
