SCI论文(www.lunwensci.com):
摘 要 :分类讨论思想是初中数学解题中的重要思想方法,是中考的热门考点. 为使学生掌握 分类讨论思想在解题中的应用思路与技巧,在讨论中做到不重不漏,提高解题正确率,应注重结合 不同题型为学生讲解分类讨论思想的具体应用过程,使其积累丰富的应用经验.
关键词 :初中数学;解题;分类讨论思想;应用
应用分类讨论思想解答初中数学习题的难点在 于如何找到分类讨论的分界点. 不同的题型寻找讨 论分界点的方法存在较大差别,因此教学中应做好 相关习题题型的归纳以及分类讨论思想在解题中的 具体应用,给学生带来良好的解题启发.
1 用于求解绝对值中的参数
例 1 有理数 x,y 满足 | x | + |y| =13,| x +y| = 1,求 x 的值.
解析 ∵ | x | + |y| =13,| x +y| =1,| x +y| ≠ | x |+ |y |,可知 x、y 必定异号. 接下来需要进行分类 讨论 :
(1)当 x > 0,y < 0 时,则 x -y = 13,y =x -13, ∴ |2x-13 | =1,则 2x-13 = ±1,解得 x=6 或 x=7;
(2)当 x <0,y >0 时,则-x +y =13,y=x +13, ∴ |2x +13 | =1,则 2x +13 = ± 1,解得 x = -6 或 x=-7;
反思 解答绝对值问题时为更好的找到分类讨 论的分界点,应认真审题,结合所学,充分挖掘隐含 条件. 如题目中判断出 x、y 异号是分类讨论的关键.
2 用于求解函数中的参数
2. 1 遇有坐标轴名称不明确时需讨论
例 2 已知正比例函数 y =k1 x 与一次函数 y= k2 x +b 图象经点 P(-2,1),其中一次函数 y=k2 x + b 图象与 y 轴交点坐标为 A(0,3),求直线 y=k1 x 与 直线 y=k2 x +b 与坐标轴围成三角形的面积.
解析 ∵ 直线 y =k1 x 经点 P( -2,1 ),∴ 正比例函数解析式为 y=

x.
∵ 直线 y=k2 x +b 经点 P( -2,1)与 A(0,3), ∴ 一次函数解析式为 y=x +3 .
(1)两条直线与 y 轴围成△AOP,如图 1 所示,过点 P 作 PM⊥OA,垂足为 M,∴ S △AOP =
 OA ·PM=3.
OA ·PM=3.
(2)两条直线与 x 轴围成△BOP,如图 1 所示,
过点 P 作 PN⊥x 轴,垂足为 N,设直线 y=x +3 且与 x 轴相交于点 B,∴ S △BOP = OB ·PN=
OB ·PN= .
.
由此可知,两条直线与坐标轴围成三角形面积
为 或 3 .
或 3 .
反思 从已知条件可直接求出一次函数与正比 例函数解析式,然而在求两条直线与坐标轴围成三 角形面积时并未直接指出是 x 轴或 y 轴围成的三角 形,所以可采取分类讨论思想.
2. 2 遇有点位置不明确时需讨论
例 3 在平面直角坐标系中,已知点 A( -3, 0),B(2,6),x 轴上有一点 C 满足 S △ABC =12,求点 C 坐标.
解析 ∵ S △ABC =12,∴ AC=4.
(1)当点 C 在点 A 右侧,点 C 坐标为(1,0);
(2)当点 C 在点 A 左侧,点 C 坐标为( -7,0) . 由此可知,点 C 坐标为(1,0)或(-7,0) .
反思 由于无法确定 x 轴上点 C 位置,故而需要采取分类讨论.
2. 3 遇有 k、b 符号不确定时需讨论
例 4 一次函数 y =kx +b 图象与 x 轴、y 轴分别交于 A 与 B 两点,S △AOB =4,且 OA :OB =1 :2,求该 一次函数解析式.
解析 ∵ S △AOB =4,∴

OA ·OB=4.
∴ OA · OB=8 .
∵ OA∶ OB =1 ∶ 2
∴ 设 OA =x,OB=2x (x > 0),则 x ·2x =8,即 x =2(-2 舍去) .
∴ OA =2,OB=4.
(1)当 k > 0,b > 0 时,一次函数 y =kx +b 图象 经第一/二/三象限,此时 A( -2,0),B(0,4),一次 函数解析式为 y=2x +4. 同理可得 :
(2) 当 k > 0,b < 0 时,一 次 函 数 解 析 式 为 y=2x-4.
(3)当 k <0,b > 0 时,一次函数解析式为 y=-2x +4
(4)当 k < 0,b < 0,一 次 函 数 解 析 式 为 y = -2x-4.
由此可知,一次函数解析式为 y=2x ± 4 或 y = -2x ±4
反思 因无法确定k 与 b 符号且二者的值存在 较多可能,故而需要分类讨论.
2. 4 遇有增减性不明确时需讨论
例 5 已知一次函数 y=kx +b 自变量 x 取值范 围为-2≤x ≤6,对应函数值 y 的取值范围为 -11 ≤ y ≤9,求一次函数解析式.
解析 (1)若函数 y =kx +b 为增函数,那么一 次函数 y=kx +b 图象两端点坐标为( -2,-11)与 (6,9),一次函数解析式为 y=2. 5x-6.
(2)若函数 y =kx +b 为减函数,函数 y =kx +b 图象两个端点坐标为( -2,9)与(6,-11 ),一次函 数解析式为 y=-2. 5x +4.
由此可知,一次函数解析式为 y=2. 5x -6 或 y =2. 5x +4.
反思 由于未明确一次函数 y =kx +b 中 k 值 的符号,所以无法确定函数增减性与其对应两个端 点坐标,需采取分类讨论.
3 用于求解图形中的线段长度
例 6 一张直角三角形纸张 ABC,∠C=90°,AB =10,AC=6,点 D 为 BC 边上任意一点,沿着过点 D 的直线折叠,使得点 C 落在斜边 AB 上的点 E 上,若 当△BDE 为直角三角形时,CD 的长为

.
解析 ( 1 ) ∠BDE =90°时,对应的情境如图 2 所示,∵ ∠C =90°,AB = 10,AC =6,由勾股定理得
到 :BC= 102-62 =8,根据题意可知四边形 CDEF为正方形. 设 CD=x,则 BD =8 -x,AF=6 -x,易得△AEF ∽ △EDB,∴ AF/ED = EF/DB, 即 

(2)当∠DEB=90°时,对应的情境如图 3 所示,
连接 AD,则可知△ACD≌AED,CD =DE,AC =AE = 6,设 CD=x,则 BD =8 -x,BE = 10 -6 =4,则在直角△DEB 中,由勾股定理得到 :x2 +42 = (8 -x )2,解 得 x =3 . 综上可知 CD 的长为 3 或  .
.
反思 遇到几何中的折叠问题时应冷静分析, 保证考虑问题的全面性. 必要时要画出相关草图辅 助分析,求解出满足题干情境的线段长度.
4 用于求解函数图象中点的坐标
例 7 如图 4,已知抛物线 y =x2 -2x -3 的顶 点为 E,且和 x 轴正半轴交于点 C,在 y 轴上存在一 点 D,满足 DC=DE,若在直线 DE 上存在一点 P,使得以 C、D、P 为顶点的三角形和△DOC 相似,求出 所有可能的点 P 的坐标.
解析 根据已知条件容易求得 C(3,0),E(1,
-4),设点 D(0,x ),由 DC =DE,可知 
 解得 x =-1,则点 D 的坐标为 (0,-1),则 CD= . 设过 DE 的直线为 y =kx - 1,将 E 点坐标代入得到 k = -3,∴ y = -3x -1 . 过点 E 作 EF 垂直于 y 轴,垂足为 F,如图5 所示,容易 证得△DFE≌△COD,∴ ∠FDE = ∠OCD,∠CDO = ∠DEF,∵ ∠OCD+ ∠ODC=90°,即∠FDE+ ∠ODC
解得 x =-1,则点 D 的坐标为 (0,-1),则 CD= . 设过 DE 的直线为 y =kx - 1,将 E 点坐标代入得到 k = -3,∴ y = -3x -1 . 过点 E 作 EF 垂直于 y 轴,垂足为 F,如图5 所示,容易 证得△DFE≌△COD,∴ ∠FDE = ∠OCD,∠CDO = ∠DEF,∵ ∠OCD+ ∠ODC=90°,即∠FDE+ ∠ODC=90° ∴ CD⊥DE.
(2) 当 OC 和 DP 为 对 应 边 时,由 △CDP ∽
△DOC,OC/DP= OD/DC,容易求得 PD =3 ,因 点 P 在 DE 上, 设 点 P ( x0,- 3x0-1 ), 则
=
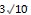 ,解得 x0 =± 3,则对应点 P 的坐标为(3,-10)或( -3,8) .
,解得 x0 =± 3,则对应点 P 的坐标为(3,-10)或( -3,8) .
综上,满足条件的点 P 的坐标有 : (

,-2) 、
( 
,
0) 、(3,-10) 、( -3,8) .
反思 求解函数图象中点的坐标问题难度一般 较大,解题时应注重联系所学的一次函数图象、二次 函数图象、图形的全等与相似等知识点,尤其当对应 边不明确时应注重分类讨论. 根据图形的全等、相似 性质构建相关的等式关系,为求解点的坐标做铺垫.
为使学生掌握应用分类讨论思想解题的技巧, 既要注重为学生讲解相关的理论与例题,又要要求 学生做好学习的总结,把握不同题型分类讨论的注 意事项以及相关细节. 同时,要求学生结合自身学习 的薄弱点,及时进行针对性的训练,不断提高运用分类讨论思想解题的熟练程度.
参考文献 :
[ 1 ] 张进华,朱树方. 分类讨论思想在侧重教学中的 应用 策 略 探 讨 [ J ] . 考 试 周 刊,2021 ( 26 ) : 13 -14 .
[2 ] 刘美. 浅析分类思想在初中数学教学中的运用 [J ] . 科技视界,2021 (06 ) :167 -168 .
[3 ] 高飞. 分类讨论思想在初中数学解题教学中的 运用探究[J ] . 中学课程辅导(教师通讯),2020 (24 ) :101 -102 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/42780.html


 x.
x. OA ·PM=3.
OA ·PM=3. OB ·PN=
OB ·PN= .
. 或 3 .
或 3 . OA ·OB=4.
OA ·OB=4.
 .
.

 .
.

 解得 x =-1,则点 D 的坐标为 (0,-1),则 CD= . 设过 DE 的直线为 y =kx - 1,将 E 点坐标代入得到 k = -3,∴ y = -3x -1 . 过点 E 作 EF 垂直于 y 轴,垂足为 F,如图5 所示,容易 证得△DFE≌△COD,∴ ∠FDE = ∠OCD,∠CDO = ∠DEF,∵ ∠OCD+ ∠ODC=90°,即∠FDE+ ∠ODC
解得 x =-1,则点 D 的坐标为 (0,-1),则 CD= . 设过 DE 的直线为 y =kx - 1,将 E 点坐标代入得到 k = -3,∴ y = -3x -1 . 过点 E 作 EF 垂直于 y 轴,垂足为 F,如图5 所示,容易 证得△DFE≌△COD,∴ ∠FDE = ∠OCD,∠CDO = ∠DEF,∵ ∠OCD+ ∠ODC=90°,即∠FDE+ ∠ODC 因点 P 在 DE 上, 设 点 P ( x0,-3x0-1 ), 则
因点 P 在 DE 上, 设 点 P ( x0,-3x0-1 ), 则 =
= ,解得 x0 = ±
,解得 x0 = ± ,则对应点 P的坐标为(
,则对应点 P的坐标为( -2)或( -
-2)或( - , 0) .
, 0) . =
= 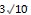 ,解得 x0 =± 3,则对应点 P 的坐标为(3,-10)或( -3,8) .
,解得 x0 =± 3,则对应点 P 的坐标为(3,-10)或( -3,8) . ,-2) 、(
,-2) 、(  ,0) 、(3,-10) 、( -3,8) .
,0) 、(3,-10) 、( -3,8) .