SCI论文(www.lunwensci.com)
摘要:复习课是数学课堂教学的重要课型,“如何创新复习课教学”也一直是热点问题.在数学学科育人理念的指引下,文章以《中心对称图形——平行四边形》单元复习课为例设计和实施教学,探索“问题驱动式”教学模式在初中数学复习课教学中的实践研究,以期提升学生核心素养,发挥数学学科育人价值.
关键词:问题驱动,复习课教学,核心素养,育人价值
复习课是初中数学教学的重要组成部分,复习课不但要将碎片化的知识串联起来,构建知识网络体系,而且还要寻求学生思维增长点,提升学生数学核心素养.所以,在以“学生为主体”“学科育人”理念的指引下,我们尝试创新初中数学复习课的教学模式,建立一种以学生为主体、以问题为起点驱动学生思考,以学生即时性生成资源促发课堂生长,使得人人能够参与其中,不同学生获得不同发展的创新复习课教学模式.本文以苏科版八年级下册第九章《中心对称图形——平行四边形》单元复习课为例,呈现问题驱动式初中数学复习课教学实践,以供研讨,不足之处,敬请批评指正.
1问题设计
问题驱动式教学模式首要的是问题设计,这里所谈到的问题是一节课中的主问题,是要解决的主要目标.本节复习课设计了两个主问题,具体如下:问题1请用尺规作一个平行四边形,并说说你的作图依据.
设计意图:通过用尺规作平行四边形,促使学生思考平行四边形的不同判定条件,引导学生建立知识之间的联系,驱动学生自主构建本章的知识体系.与教师主导下的“本章知识回顾”相比,学生自然更对这样一种新的教学方式感兴趣.另外,这样的教学方式使得每一个学生都能参与进来,学习能力较弱的学生也至少能想到一种方法,学习能力较强的学生不但可以想到多种解法,而且可以利用时间充分思考、联系、整合,建立知识网络体系.
问题2请用本章所学知识证明定理:直角三角形斜边上的中线等于斜边的一半.
设计意图:将本章的知识嫁接到一个老问题上,一是激发起学生的思考兴趣,二是引导学生学会串联贯通.从命题角度而言,很多题目不是凭空产生的,恰恰是从老问题、从教材中联想变化而来的.我们需要将这种串联贯通的思想传递给学生,在“移花接木”中提升学生的数学核心素养,发挥数学学科的育人价值.
2教学实施
问题是数学的心脏,是思考的起点.如何实施问题驱动式复习课教学呢?基于问题捕捉利用学生的即时性生成资源才是关键.下面具体呈现本节课的教学实践过程.
问题1请用尺规作一个平行四边形,并说说你的作图依据.
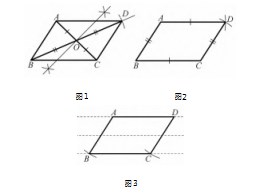
学生依托平行四边形的判定条件生成了不同的作法:一是根据“对角线互相平分的四边形是平行四边形”作图,或利用平行四边形的中心对称性,从图形运动的角度构建新的图形,即作ΔABC关于点O的中心对称作图,如图1所示;二是利用“两组对边相等的四边形是平行四边形”构建图形,如图2所示;有个别学生利用“一组对边平行,另一组对边相等”构建图形,如图3所示.生:图3是有问题的,这种作法中有一组对边平行,但是没有用尺规作图,是简单利用练习纸上的格线,然后又作了一组对边相等,这种作法得到的四边形ABCD不一定是平行四边形.首先,没有这样的判定条件,此外,可以举出反例,也就是作DC=AB时,以点D为圆心画弧,这条弧与直线BC有两个交点,所以得到的四边形有可能是平行四边形,也有可能是等腰梯形.
师:还有其他的作法吗?
生:还可以根据“一组对边平行且相等”和“两组对边分别平行”来作图.师:平行四边形是中心对称图形,它还具备哪些性质呢?你是如何思考的呢?
生:可以从图形元素的角度来看,我们知道平行四边形两组对边分别平行且相等、对角线互相平分、两组对角相等.
师:平行四边形的判定条件和性质有什么关联呢?
生:逆向思考,是互逆命题.
师:本章还谈到了哪些呢?
生:特殊的平行四边形.比如,矩形、菱形、正方形,以及三角形中位线定理.
师:平行四边形是一种结构不稳定的平面图形,特殊的平行四边形其实是一般平行四边形运动变化过程中的某一个特殊的状态,在运动中图形元素的特性也会随之发生变化.比如:拉动平行四边形变成矩形时,所有的角变成了直角,对角线被拉到相等;拉伸平行四边形一组对边变成菱形时,对角线变成互相垂直.
问题2请用本章所学知识证明定理:直角三角形斜边上的中线等于斜边一半.
师:证明文字命题首先要做什么?
生:根据题意画出图形,写出已知求证.
师:请大家先将文字命题符号化处理,已知什么?求证什么?
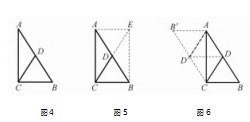
生:已知:如图4,在RtΔACB中,CD是AB边上中线.求证:CD=AB.
师:你会想到本章的哪些知识呢?如何利用其证明呢?
学生能想到矩形,但是构造辅助线时采用“过A,B两点作BC,AC的平行线交于点E,再连接CE”,学生们也发现了C,D,E三点并不确定共线.
师:此路不通换条路,请同学们从图形的构造方法入手,能不能得到证明方法?
生:如图5,延长CD到点E,使DE=CD,连接AE,BE.由对角线互相平分可证四边形ACBE是平行四边形,进一步由∠ACB=90°证得四边形ACBE是矩形,从而易证CD=CE=AB.师:类比构造平行四边形的方法,构造矩形的方法不唯一.那么,同学们还有不同的证法吗?
生:平行四边形是本章的主题.如图6,过A,C分别作BC,AB的平行线交于点B',取B'C的中点D',连接AD'.根据作图,可证四边形AB'CB和四边形AD'CD是平行四边形.进一步可证明四边形AB'D'D是平行四边形,从而得到DD'∥AB',易证AC⊥DD',于是有四边形AD'CD是菱形,最终得到CD=AD=AB.
师:你的想法好高级!实际上,这种证法是将证明CD=AB转化成了证明CD=AD,进一步联想到了菱形的邻边相等.该菱形不能直接作出,而是通过平行四边形AB'CB搭建的.
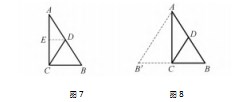
师:请同学们从所证结论“CD=AB”进一步
思考,在哪里见到过“倍半关系”呢?学生自然想到了本章所学的中位线,并产生了不同的构建中位线的方法和证明方法.图7是“截半”构造了中位线DE,易证RtΔAED≌RtΔCED,从而有CD=AD=AB.图8是“倍长”BC,也可以倍长AC,证明过程类似.师:同学们的想法真的都非常棒,让老师看到了同学们思维里的光!经过对一个已学定理的证明,相信同学们都一定程度上经历了串联贯通!这也是数学复习的核心目标.
3教学反思
3.1以问促联
郑毓信教授说:“基础知识贵在求联,基本技能贵在求通.[1]”这句话明示了复习课的核心目标.那么,如何在复习课中引导学生自主联系构建知识网络?如何在复习课中引导学生促通暗藏于知识网络中的思想方法?笔者认为,数学学习的过程是一个解决问题的过程,复习亦然,故而我们要根据复习课的目标设计好主问题,好的问题就如同一颗好的种子,能生根也能发芽,学生的知识便顺着藤蔓陈铺开来,学生的思维沿着知识藤蔓一路展叶、蓓蕾开花.以问题促发学生思考,在解决问题中让知识串联和思维方法协同生长!
3.2以问引思
美国著名数学教育家G.波利亚说:“一个专心的认真备课的教师能够拿出一个有意义但又不太复杂的题目,去帮助学生挖掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域.[2]”我想本节课中问题2不失为一个有意义但又不太复杂的问题,这一道题打通了本章的所有关节,构建图形、平行四边形、特殊平行四边形、中位线……直角三角形的斜边中线和平行四边形到底有什么关联?这样的问题,增加了复习课的趣味性,调动了学生思考的积极性,引发了学生深度思考,在一个个生成的解法中持续激发学生的思考力,最终在各种解法中破解直角三角形斜边上的中线与平行四边形之间的渊源,每个人获得了不同程度的发展,获得不同程度的成功与喜悦[3].
参考文献:
[1]郑毓信.认清形势砥砺前行(续):寄语初中数学教师[J].中学数学教学参考(中旬),2020(8):2-4.
[2]G.波利亚.怎样解题[M].涂泓,冯承天,译.上海:上海科技教育出版社,2011.
[3]卜以楼.生长构架:复习课的理念创新[J].中学数学(初中版),2016(10):44-46.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/73869.html